Решение кубического уравнения бинарный поиск

Разбор задач. Бинпоиск_1

Здравствуйте, уважаемые хабровчане. Серия статей содержит разбор задач, которые дают в 8 классе на уроках информатики в Челябинском физико-математическом лицее №31. Немного истории… Наш лицей — одно из сильнейших учебных заведений России, который в рейтинге по конкурентоспособности выпускников занимает 5 место, уступив школам Москвы и Санкт-Петербурга. Ученики регулярно побеждают на олимпиадах всероссийского и международного уровня.
Данная статья лишена теории, она содержит только способы решения задач. Подробно про бинпоиск описано здесь.
Так вот, перейдем к задачам. Эти задачи подразумевают собой использование бинарного поиска, в том числе бинпоиска по ответам. Как мы знаем бинпоиск — это алгоритм поиска объектов по заданному признаку в множестве объектов. Применяем для отсортированных по возрастанию/убыванию списков. Всего 4 задачи, 2 из которых направлены на применение «алгоритма без изюминок».

Левый и правый двоичный поиск

В этой задаче сначала нужно считать длины первой и второй строки, затем каждую следующую строку записать в список. После мы берем каждый элемент второго списка и ищем для него правую и левую границу. Можно заметить, что если число отсутствует в списке, итоговые значения левой границы и правой границы в левом и правом бинпоиске равны.

Приближенный двоичный поиск

Вот эта задачка с изюминкой! Тут надо так преобразовать поиск, чтобы выполнялось даже для чисел, которых нет в данном для поиска списке. Здесь мы также ищем середину в “граничном списке”, затем элемент, который посередине сравниваем с числом, если он меньше него, мы записываем в левую границу(который индекс) индекс середины + 1(то есть не включаем прошлую середину в граничный список), в ином случае в правую границу записываем индекс середины. Все это делаем, пока левая граница меньше правой. После нахождения left и right рассматриваем случай, когда числа нет в списке и расстояние до того, что левее меньше или равно, чем то, что правее. Поэтому выводим a[left — 1], в ином случае a[left].

Квадратный корень и квадратный квадрат

Тадам! Задача на бинарный поиск по ответу. Для начала из библиотеки math подключим функцию sqrt, которая вычисляет квадратный корень, после определим для левой границы 0, а для правой 1e10, то есть 10 миллиардов, исходя из ограничений, которые указаны в условии. Далее как в типичном бинпоиске ищем середину, позже сравниваем. Но что тут интересного? Тут middle — это x в уравнении. Ввиду этого определяем значение уравнения и сверяем с реальным ответом(т.е. С). Ну и двигаем границы, до тех пор, пока разность границ не будет меньше или равна 10-ти миллиардным, это и есть точность измерения. Позже умножаем на миллион, округляем, переводим в int и вещественное деление на тот же миллион.

Очень Легкая Задача

Разбор на эту задачу уже есть, поэтому приложу только код.

Анализ алгоритма

Локализируем корень равнения f( x) = 0. Для этого найдем такое r, что f(- r) * f( r) r = 1, будем на каждом шаге увеличивать r в два раза пока не будет выполняться неравенство f(- r) * f( r) [-1; 1], [-2; 2], [-4; 4], [- 8 ; 8 ], …. пока не найдем интервал в котором лежит корень уравнения.

Положим l = — r. Далее на промежутке [ l; r] при помощи бинарного поиска (деления отрезка пополам) ищем корень.

Реализация алгоритма

Объявим константу епсилон .

#define EPS 1e-12

Объявим функцию, вычисляющую кубический многочлен.

double f( double x)

return a*x*x*x + b*x*x + c*x + d;

Основная часть программы. Читаем входные данные.

Находим границы [ l; r], в которых лежит искомый корень. Положим изначально r = 1. Будем последовательно увеличивать r в два раза, пока искомый корень не будет находиться в промежутке [- r; r] (для этого необходимо, чтобы функция f( x) принимала противоположные по знаку значения на концах интервала). После чего положим l = — r.

while (f(r) * f(-r) >= 0) r *= 2;

При помощи бинарного поиска ищем корень уравнения f( x) = 0 на промежутке [ l; r].

Решение кубического уравнения бинарный поиск

Требуется реализовать алгоритм бинарного поиска.

В первой строке входных данных содержатся натуральные числа $N$ и $K$ $(0 YES , если это число встречается в первом массиве и NO в противном случае.

Обратите внимание, требуется именно бинарный поиск. Решение с множествами, словарями, map’ами, set’ами и т.п. засчитываться не будут.

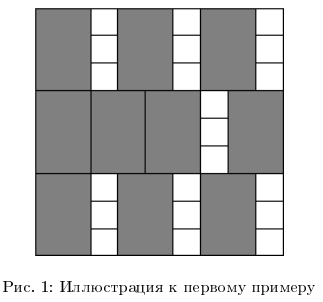
B: Левый и правый бинарный поиск

Дано два списка чисел, числа в первом списке упорядочены по неубыванию. Для каждого числа из второго списка определите номер первого и последнего появления этого числа в первом списке. Реализуйте для этого две функции: левый и правый бинарный поиск.

В первой строке входных данных записано два числа $N$ и $M$ $(1 \leqslant N,M \leqslant 20000)$. Во второй строке записано $N$ упорядоченных по неубыванию целых чисел — элементы первого списка. В третьей строке записаны $M$ целых неотрицательных чисел — элементы второго списка.

Программа должна вывести $M$ строчек. Для каждого числа из второго списка нужно вывести номер его первого и последнего вхождения в первый список. Нумерация начинается с единицы. Если число не входит в первый список, нужно вывести одно число $0$.

C: Бинарный поиск — подсчёт количества элементов, равных данному числу

Требуется определить в заданном массиве количество элементов, равных искомому числу.
В первой строке вводится количество чисел в массиве — натуральное число $N$, не превосходящее $10^5$.
Во второй строке вводятся $N$ натуральных чисел, не превосходящих $10^9$, каждое следующее не меньше предыдущего.
В третьей строке вводится количество искомых чисел $M$ — натуральное число, не превосходящее $10^6$.
В четвертой строке вводится $M$ натуральных чисел, не превосходящих $10^9$.

Для каждого запроса выведите в отдельной строке одно число: количество элементов массива, равных числу-запросу. Элементы массива нумеруются с единицы.
Если в массиве нет такого числа, выведите 0.

D: Приближённый бинарный поиск

Реализуйте алгоритм приближенного бинарного поиска.

В первой строке входных данных содержатся числа $N$ и $K$ $(0

E: Вещественный бинарный поиск

Найдите такое число $x$, что $x^2+\sqrt=C$. Найденное значение $x$ должно быть вычислено с точностью не менее $6$ знаков после точки.

В единственной строке содержится вещественное число $C$ $(1.0 \leqslant C \leqslant 10^<10>)$.

Выведите одно число — искомый $x$.

F: Корень кубического уравнения

Дано кубическое уравнение $ax^3+bx^2+cx+d=0$ $(a\ne0)$. Известно, что у этого уравнения ровно один корень. Требуется его найти.

Во входных данных через пробел записаны четыре целых числа: $-1000 \leqslant a,b,c,d \leqslant 1000$.

Выведите единственный корень уравнения с точностью не менее $4$ знаков после десятичной точки.

G: Ксерокопии

Сегодня утром жюри решило добавить в вариант олимпиады еще одну, Очень Легкую Задачу. Ответственный секретарь Оргкомитета напечатал ее условие в одном экземпляре, и теперь ему нужно до начала олимпиады успеть сделать еще $N$ копий. В его распоряжении имеются два ксерокса, один из которых копирует лист за $x$ секунд, а другой — за $y$. Разрешается использовать как один ксерокс, так и оба одновременно. Можно копировать не только с оригинала, но и с копии.

Помогите ему выяснить, какое минимальное время для этого потребуется.

На вход программы поступают три натуральных числа $N$, $x$ и $y$, разделенные пробелом ($1 \leqslant N \leqslant 2\cdot10^8, 1 \leqslant x, y \leqslant 10$).

Выведите одно число — минимальное время в секундах, необходимое для получения $N$ копий.

H: Дипломы

Вычислить наименьшую сторону квадрата, в который можно уложить без наложений $N$ одинаковых прямоугольников данного размера. Стороны прямоугольников параллельны сторонам квадрата, поворачивать прямоугольники нельзя.

Входной файл содержит три целых числа: $w,h,N$ $(1 \leqslant w,h,n \leqslant 10^9)$ — ширина и высота прямоугольника и их количество.

В выходной файл необходимо вывести ответ на поставленную задачу — длину стороны квадрата.

I: Провода

Дано $N$ отрезков провода длиной $L_1, L_2, \ldots, L_N$ сантиметров.

Требуется с помощью разрезания получить из них $K$ равных отрезков как можно большей длины, выражающейся целым числом сантиметров. Если нельзя получить $K$ отрезков длиной даже $1$ см, вывести $0$.

В первой строке находятся числа $N$ и $K$ $(1 \leqslant N \leqslant 10000, 1 \leqslant K \leqslant 10000)$. В следующих $N$ строках — $L_1,L_2,\ldots,L_N$ $(100 \leqslant L_i \leqslant 10^7)$, все числа целые, по одному числу в строке.

Требуется вывести одно число — полученную длину отрезков.

J: Коровы — в стойла!

На прямой расположены стойла, в которые необходимо расставить коров так, чтобы минимальное расcтояние между коровами было как можно больше.

В первой строке вводятся числа $N$ $(2

K: Билеты

В одной театральной кассе есть в продаже билеты любой стоимости, выражающейся натуральным числом. При покупке билетов по цене за билет от $A$ до $B$ рублей включительно нужно дополнительно оплатить сервисный сбор в размере $C$ процентов от номинальной стоимости билетов (сервисный сбор не обязательно выражается целым числом рублей, но всегда выражается целым числом копеек). При покупке билетов стоимостью менее $A$ рублей за билет, а также более $B$ рублей за билет, сервисный сбор не берется.

У вас есть $X$ рублей и вам нужно $K$ билетов одинаковой цены (цена обязательно должна выражаться натуральным числом рублей, $0$ не считается натуральным). Билеты какого самого дорогого номинала вы можете себе позволить?

Вводятся целые $A,B,C,X,K$ $(1 \leqslant A \leqslant B \leqslant 10^9,0 \leqslant C \leqslant 1000,0 \leqslant X \leqslant 10^9,1 \leqslant K \leqslant 100000)$.

Если на имеющиеся деньги невозможно приобрести ни одного билета, выведите 0. Иначе выведите натуральное число — номинальную стоимость приобретённых билетов.

L: Лифт

Высокое здание, состоящее из $N$ этажей, оснащено только одним лифтом. Парковка находится ниже фундамента здания, что соответствует одному этажу ниже первого. Этажи пронумерованы от $1$ до $N$ снизу вверх. Про каждый этаж известно количество человек, желающих спуститься на лифте на парковку. Пусть для $i$-го этажа эта величина равна $A_i$. Известно, что лифт не может перевозить более $C$ человек единовременно, а также то, что на преодоление расстояния в один этаж (не важно, вверх или вниз) ему требуется $P$ секунд. Какое наибольшее количество человек лифт может перевезти на парковку за $T$ секунд, если изначально он находится на уровне парковки?

В первой строке входного файла содержатся целые числа $N,C,P,T$. Вторая строка содержит последовательность $N$ целых чисел $A_1,A_2,\ldots,A_N$.

Ограничения: $1 \leqslant N \leqslant 100,1 \leqslant C \leqslant 10^9,1 \leqslant P \leqslant 10^9,1 \leqslant T \leqslant 10^9, 0 \leqslant A_i \leqslant 10^9$. Сумма всех значений последовательности не превосходит $10^9$.

Выведите наибольшее количество человек, которое лифт успеет перевезти на парковку.

M: Шарики на детском празднике

Организаторы детского праздника планируют надуть для него $M$ воздушных шариков. С этой целью они пригласили $N$ добровольных помощников, $i$-й среди которых надувает шарик за $T_i$ минут, однако каждый раз после надувания $Z_i$ шариков устаёт и отдыхает $Y_i$ минут.

Теперь организаторы праздника хотят узнать, через какое время будут надуты все шарики при наиболее оптимальной работе помощников, и сколько шариков надует каждый из них. Если помощник надул шарик, и должен отдохнуть, но больше шариков ему надувать не придётся, то считается, что он закончил работу сразу после окончания надувания последнего шарика, а не после отдыха.

В первой строке входных данных задаются числа $M$ и $N$ $(0 \leqslant M \leqslant 15000,1 \leqslant N \leqslant 1000)$. Следующие $N$ строк содержат по три целых числа — $T_i,Z_i$ и $Y_i$ соответственно $(1 \leqslant T_i,Y_i \leqslant 100,1 \leqslant Z_i \leqslant 1000)$.

Выведите в первой строке число $T$ — время, за которое будут надуты все шарики. Во второй строке выведите $N$ чисел — количество шариков, надутых каждым из приглашенных помощников. Разделяйте числа пробелами. Если распределений шариков несколько, выведите любое из них.

N: Дремучий лес (задача на тернарный поиск максимума/минимума унимодальной функции)

Чтобы помешать появлению СЭС в лагере, администрация ЛКШ перекопала единственную дорогу, соединяющую «Берендеевы поляны» с Судиславлем, теперь проехать по ней невозможно. Однако, трудности не остановили инспекцию, хотя для СЭС остается только одна возможность — дойти до лагеря пешком. Как известно, Судиславль находится в поле, а «Берендеевы поляны» — в лесу.

1. Судиславль находится в точке с координатами $(0,1)$.
2. «Берендеевы поляны» находятся в точке с координатами $(1,0)$.
3. Граница между лесом и полем — горизонтальная прямая $y=a$, где $a$ — некоторое число $(0 \leqslant a \leqslant 1)$.
4. Скорость передвижения СЭС по полю составляет $V_p$, скорость передвижения по лесу — $V_f$. Вдоль границы можно двигаться как по лесу, так и по полю.

Администрация ЛКШ хочет узнать, сколько времени у нее осталось для подготовки к визиту СЭС. Она попросила вас выяснить, в какой точке инспекция СЭС должна войти в лес, чтобы дойти до «Берендеевых полян» как можно быстрее.

В первой строке входного файла содержатся два положительных целых числа $V_p$ и $V_f$ $(1 \leqslant V_p,V_f \leqslant 10^5)$. Во второй строке содержится единственное вещественное число — координата по оси $Oy$ границы между лесом и полем $a$ $(0 \leqslant a \leqslant 1)$.

В единственной строке выходного файла выведите вещественное число с точностью не менее $8$ знаков после запятой — координата по оси $Ox$ точки, в которой инспекция СЭС должна войти в лес.