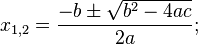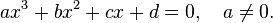Решение кубического уравнения си шарп

Поиск по сайту

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений — как точных, так и численных (приближенных).

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

где выражение D = b 2 − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

• Если D>0, то корней уравнения будет два и оба они будут действительными числами;
• Если D=0, то будет лишь один дейсвительный корень уравнения;
• Если D 2 +10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
• x 2 -8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
• x 2 -5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

На выходе получим:

5x^2 — 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 — 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 — 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

• x^3 — 6x^2 + 11x — 6 = 0
• x^3 — 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

Напишем программу для тестирования метода:

x^3 — 6x^2 + 11x — 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 — 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Решение биквадратных уравнений

Биквадратное уравнение — уравнение четвёртой степени вида

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x 2 сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

• 5x^4 — 10x^2 + 200 = 0
• x^4 — 8x^2 + 16 = 0
• x^4 — 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

Напшем программу для тестирования метода:

На выходе получим такие результаты:

5x^4 — 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 — 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 — 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.

Полное решение кубического уравнения (формула Кардано)

Необходимо решить кубическое уравнение с действительными коэффициентами: ax 3 + bx 2 + cx + d = 0 .

По основной теореме алгебры оно имеет три корня (4 различных типа).

Формула была украдена у Тартальи и опубликована Джероламо Кардано (тем самым изобретателем карданного вала) в книге «Великое искусство» в 1545 году. Описание алгоритма доступно в Интернете, однако программная реализация имеет некоторые нюансы, связанные с необходимостью анализа исходных данных. Вот что получилось:

Входными параметрами метода являются коэффициенты a, b, c, d; по ссылке возвращается тип корней (tip=1,2,3,4) и их значения (p1,p2,p3):

Для типа 1 (tip=1) имеется один действительный и два комплексных корня: x1=p1; x2=p2+i*p3; x3=p2-i*p3, где i — мнимая единица.
Тип 2 — три различных действительных корня, тип 3 — один отличающийся и два кратных действительных корня, тип 4 — три кратных действительных корня, для всех типов (tip=2,3,4) x1=p1, x2=p2, x3=p3.
Если кубическое уравнение является характеристическим уравнением исходного линейного дифференциального уравнения 3 степени, то для его решения важно знать именно тип решения (tip).

Для тестирования метода используйте следующую программу:

Минимальный набор тестов:
a, b, c, d:
187.5, 50, 10, 1 -> тип 1
1, 6, 3, -10 -> тип 2
1, 12, 36, 32 -> тип 3
3, -9, 9, -3 -> тип 4

Решение кубического уравнения / Методы решения нелинейных уравнений и их систем / Алгоритмы