Решение квадратичных неравенств системы уравнений с двумя неизвестными

Неравенства и системы неравенств с двумя неизвестными

Вы будете перенаправлены на Автор24

Решение неравенств с двумя неизвестными, а тем более их системы, на первый взгляд кажется сложной задачей. Рассмотрим алгоритм, с помощью которого можно легко справиться с этой задачей.

Неравенство с двумя неизвестными

Пусть имеется неравенство с двумя неизвестными вида $y $, $\le$, $\ge$).

Множество решений подобного неравенства можно изобразить на координатной плоскости. Для этого необходимо:

Построить график функции y=f(x), который разобьет координатную плоскость на две разные области.

Выбрать одну из этих областей и рассмотреть в ней любую точку. Проверить, выполняется ли для этой точки исходное неравенство:

• Если неравенство выполняется, следовательно, оно выполняется и для всей области, из которой выбирали точку. Таким образом, область, в которой лежит выбранная точка и есть множеством решений неравенства.
• Если неравенство не выполняется, то множество решений неравенства – область, в которой не лежит выбранная точка.

При решении строгих неравенств границы области, которыми являются точки графика функции $y=f(x)$, не включаются в множество решений, при этом граница изображается пунктирной линией. При нестрогих неравенствах границы области включаются в множество решений неравенства, при этом граница изображается сплошной линией.

Показать на графике множество точек, которое задается неравенством $xy>3$.

Построим график функции $xy=3$. Для этого разделим обе части уравнения на $х$, т.к. оно не может обращаться в нуль, что следует из уравнения (произведение числа на нуль не может равняться $3$):

График получившейся функции – гипербола, которая разобьет координатную плоскость на 2 области: одна находится между ветвями гиперболы, а другая – за ними.

Выберем из одной области любую точку, например, с координатами $(1; 2)$.

Подставим ее координаты в неравенство:

$2>3$ – неравенство неверное.

Следовательно, точки выбранной области не являются решением данного неравенства. Таким образом, решением неравенства будет другая область, из которой точку не выбирали.

Данное неравенство строгое, поэтому граничные точки, которыми являются точки графика функции y=3/x, наносятся на график пунктирной линией. Обозначим на графике множество точек, которые являются решением данного неравенства:

Готовые работы на аналогичную тему

Система неравенств с двумя неизвестными

Рассмотрим пример решения системы неравенств с двумя неизвестными.

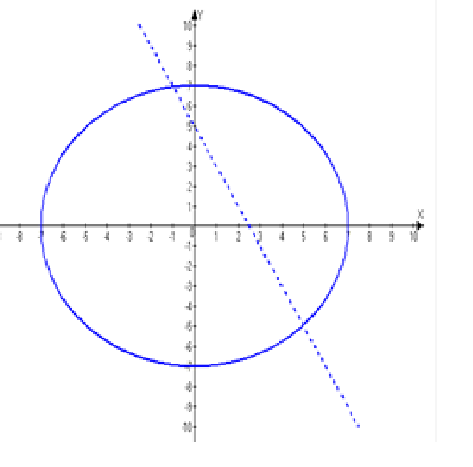
Показать на графике множество точек, которое задается системой неравенств

Построим графики функций, которые соответствуют данным неравенствам:

Изображаем функцию $x^2+y^2=49$ сплошной линией, т.к. она соответствует нестрогому неравенсту, а прямую $2х+y=5$ – пунктирной.

Рассмотрим каждое неравенство отдельно.

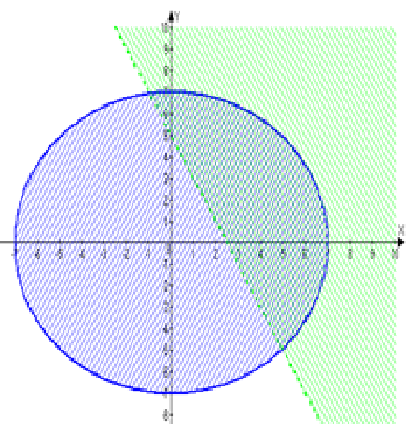
Первое неравенство $x^2+y^2 \le 49$:

Возьмем точку $(5; 8)$ выше графика данной функции. Проверим справедливость неравенства:

$89≤49$ – неравенство неверно.

Следовательно, решение данного неравенства – область, в которой не лежит выбранная точка, т.е. область внутри окружности.

Второе неравенство $2x+y > 5$:

Возьмем точку $(4; 3)$ выше графика данной функции. Проверим справедливость неравенства:

$11 > 5$ – неравенство верно.

Следовательно, решение данного неравенства – область, в которой лежит выбранная точка, т.е. область выше прямой.

Изобразим найденные решения на координатной плоскости.

Пересечение полученных областей и является решением данной системы.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 07 2021

Квадратичные неравенства с двумя неизвестными

Вещественная линия второго порядка разбивает координатную плоскость на области. В силу свойств многочленов второй степени (в частности, их непрерывности) для решения квадратичных неравенств 0,» png;base64,iVBORw0KGgoAAAANSUhEUgAAAGMAAAAWCAMAAADjCtLVAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAEUGRgWkxAdTBIaHwsVIQCAZgmgAAAexJREFUSMe9Vtty6yAMNFdJXAz//7WVgNQQx7XP6Uzz4BmE0MLuIrJtf//z8S7DuN9CoLpLAdT3dYK+roP7g/Up3GQUIovmYtLhk8NGe5NAedtUchc0POJ6TwcRRsOZ8CpsmAQf1ajhCQbUg9EQ0b3XslW3rz/Iy+SVIVs2cLWnt+FOC6OWhKEiH1hmlH1HyQPjICXqiBSA2LSRWrLKHpCinxm1Tsu+TNuFoaUmo9jJRkADwx4abDkVCcFGNFBZtqRiPUyqiMsHTkbBsG9UA7gZ5YQRNKQshauGgcFsS6z42e9cnqGq6YSf5BSUcnUOUVo4wapeGN+x1Q8ccV3tDxhs+1iuziELecOhcv0Dw02meJkliBzqI4ac4rCkGRh6toEkSWRong3HgMnnUdi/s3jU5WCPrZovajDX/X7IfnTHgcQDn4Ro17TUNavK5DvbJgdpkTFclwPkHi/efWtOyB5V0kyg9sP4msn0Cx76HUSDGmO7D+yvwWpgN2OXAyaxij3fQe6s0RGVprId1CsPSy+R4Qht2r786UPsTWSf2kF0nzoG7NbPy/NkdkdnT+5DR8/H7HgxPn8sjG6dGqednN6GMmYJi8L4sLdP96ptmvgXLt8ocP5lfyL3L815XQ4/vbUwNYz/eGvhr/4jfAHToRC+7XkJQwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> достаточно определить знак многочлена в одной внутренней точке какой-либо области. Знаки в других областях проставляются по правилу чередования знаков (аналогично методу интервалов): переходя через границу области, знак многочлена меняется на противоположный, за исключением совпадающих прямых (при переходе через них знак многочлена не меняется). В случае мнимых линий знак многочлена сохраняется на всей координатной плоскости.

Для всех вещественных линий, за исключением пары пересекающихся прямых, назовем внутренними те точки, координаты которых (в канонической системе координат) удовлетворяют неравенствам

соответственно. Другими словами, во внутренних точках левая часть канонического уравнения линии меньше правой.

Внешними точками по отношению к каждой из перечисленных линий назовем точки, для которых значения левой части канонического уравнения больше правой его части. На рис.3.59 внутренние точки отмечены минусом, а внешние — плюсом. Заметим, что для совпадающих прямых все точки, кроме точек, принадлежащих линии, являются внешними.

Учитывая пункт 9 замечаний 3.12, для уравнения (3.59) линии второго порядка в прямоугольной системе координат можно сформулировать условия, равносильные определениям внутренних и внешних точек линии.

Теорема (3.5) о внутренних и внешних точках линии второго порядка

Пусть уравнение определяет вещественную линию второго порядка, за исключением пары пересекающихся прямых.

1. Если уравнение определяет эллипс, параболу или пару параллельных прямых, то неравенству

удовлетворяют координаты всех внутренних (внешних) точек этих линий.

2. Если уравнение определяет гиперболу, то неравенству

удовлетворяют координаты всех внутренних (внешних) точек гиперболы.

Справедливы и обратные утверждения.

В самом деле, пусть уравнение определяет вещественную линию второго порядка, за исключением пары пересекающихся прямых. Тогда в канонической системе координат уравнение имеет вид (3.60): , где квадратичная функция получена из квадратичной функции в результате умножения на отличный от нуля множитель и ортогональной .замены переменных (3.62). По определению внутренние точки удовлетворяют неравенству , которое равносильно неравенству в исходной системе координат.

Если уравнение определяет эллипс, то 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAIgAAAArBAMAAABRHN0hAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAgkEnvwGfZ5TrEVHR5p1hrQAAAi9JREFUSMdjYKAH4CoRotwQjvK5BhQbwrLAmnKXsAhQIUzYL1HBENaZCyg3w+RsA+W+mbzyKsWGWBawXabYkNwFjBQbwjqFgZFi77BeZGBxoNg7JxjWKlBsyE7TNFSnKQeQbkhQSgEKf43vbDQPK5FuqjSTN5pTOyaRHNBlaALM0xkqSS4qbMHBbAbXx3GBIZbUfMEaMgtEBrnBTOF0ZQiZysDA7cDATryDTK6AKaYUVQg/FmgIMDXGHGDQ3QDkLlICAWX8ZjAeghaWzClbId4DGnKLgWFtAkMvqMgwFAQBcfyGSC6ohUY5c2YpiNJ1YGABFlt7C1jPAKOaFSm6N4LNW8BQ0QEFzbC4uMigCysuuWQ2IAzpNeC6gWZfIdSQsjQoSIaVLpcZbAtQDIGECetJBu7bDER6J+wqgy40Eph7wN6JBMcO1xUGjsvlBAOWGewAjgMMLQHQgIW4iA2YThIYuO8EWF5whisOxVVzXATH7GUuSCIPhkUx0yUGXQUGjpsZ2dPwpDlGiPMZIemjsgfsACYXePlQWT6dgYFnqjHDYjzBUAstk0IgKdYUTCKSPQNzuQEomQSgRC86OAmtvLYjexfd03s34I0PJkeIPxic8amSxV/BsWjNBXufqQCfqsX407lKgCzFBTWrE4MtxTU6kysD2xWKWycKDMx3Ka0zVICRn5tAoSGgot2Wwso4eCooj12jzBC2JmDGVr9LWfPR9i4YUBYoiuCCSpBQAxIAAnOEtmp6UwUAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> и (см. определение вида канонического уравнения). Поэтому

Если уравнение определяет гиперболу, то и . Поэтому

Если уравнение определяет параболу или пару параллельных прямых, то . Поэтому

Утверждения для внешних точек и обратные утверждения доказываются от противного.

1. Для пары пересекающихся прямых предлагаемое определение внутренних и внешних точек не годится, поскольку эта пара разбивает плоскость на «похожие» области, каждую из которых равным образом можно считать внутренней или внешней. Например, пара пересекающихся прямых разбивает плоскость на четыре прямых угла, т.е. на равные «четверти», которые «накладываются» одна на другую при помощи поворота вокруг начала координат на угол, кратный .

2. При выборе положительного направления оси канонической системы координат для параболы, заданной уравнением (3.59) вида , достаточно проверить, является ли точка с координатами внутренней. Этой точке соответствует координатный столбец в исходной системе координат, где –координатный столбец точки . Вычислим значение квадратичной функции при подстановке координат

поскольку (точка принадлежит параболе), а также , так как — особый собственный вектор параболы. Из теоремы 3.5 следует, что точка является внутренней при условии т.е. при условии

3. Из теоремы 3.5 следует, что градиент функции в точках линии уровня направлен при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQBAMAAAB0JTvnAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAwQGHQSGk6DEQ0GFSUXEDuLLtAAAAsklEQVQY02NgIAVMacAuzl2chV3Gv4G5EsFjsYQzsxhYfyOpO5gKZTB9ZGD6BqSDjY2NQUYyOUJlWIAS3xUYuL/LFwpC7HIUgUh8ZmD6r8AQ3jSdCWZamIgCQiKS4SDCnjBZhAQDQzKSxFqEHQxM1QhxGZBCzo8ghzEwcPyAOdMNYjnTKgbWf0Ba+RNUwjEFytgfwFcKpBgTINyLMA8yMNeZXwBSrBMgrjeFW6UQd5KBAQDu8yrmAuMwtgAAAABJRU5ErkJggg==» /> в сторону внешних точек эллипса или параболы, при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» /> — в сторону внешних точек гиперболы, в противном случае, при для эллипса и параболы или при для гиперболы градиент направлен в сторону внутренних точек (рис.3.60).

4. Линии уровня квадратичной функции (3.57) являются линиями второго порядка. При изменении величины параметра меняется свободный член функции , однако при этом не изменяются выражения и , а, следовательно, и корни характеристического уравнения, поскольку они не зависят от свободного члена. Поэтому тип линии уровня (эллиптический, гиперболический или параболический) сохраняется. Для всех центральных линий уровня сохраняется отношение сторон основного прямоугольника, а также эксцентриситет и фокальный параметр для эллипсов, гипербол и парабол. Вид линии может измениться, поскольку выражения и зависят от свободного члена. Например, при некоторых значениях постоянной линия может быть вещественным эллипсом, при других значениях — мнимым эллипсом, а при одном значении — парой мнимых пересекающихся прямых.

5. Линии уровня заданной квадратичной функции при различных значениях параметра имеют постоянные собственные направления, т.е. базисные векторы канонической системы координат не изменяются. Следовательно, если линии уровня центральные, то все они имеют одну и ту же систему координат. При возрастании параметра эллипсы и гиперболы изменяются гомотетично (центр гомотетии совпадает с центром линии) в направлениях, указанных на рис.3.60. Если линии уровня параболические, то все они имеют одну и ту же ось абсцисс канонической системы координат. При возрастании параметра параболы перемещаются в направлениях, указанных на рис.3.60.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение систем неравенств: линейные, квадратные и дробные.

Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).

Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5y +1/7y^2
Результат: \( 3\frac<1> <3>— 5\frac<6> <5>y + \frac<1><7>y^2 \)

При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Выберите нужный знак неравенства и введите многочлены в поля ниже.