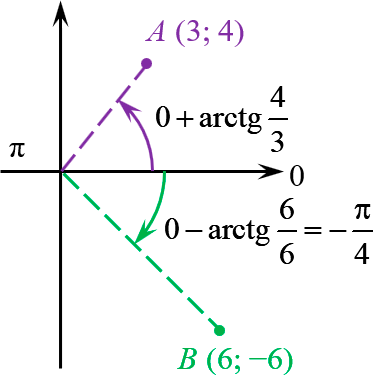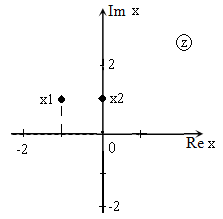Решение квадратного уравнения по формуле муавра

Формула Муавра

Содержание:

Задание комплексных чисел в тригонометрической форме удобно при выполнении над числами действий умножения, деления, возведения в степень и извлечения корня.

Найдем произведение двух комплексных чисел, записанных в тригонометрической форме; пусть

Выражения, стоящие в круглых скобках, можно упростть с помощью известных формул (115.4), (116.1):

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Доказано правило: для умножения чисел, заданных в тригонометрической форме у их модули надо перемножить, а аргументы сложить.

Это правило остается верным для любого количества сомножителей.

Примеры с решением

Пример 1.

Найти произведение чисел

Решение:

Так как деление—действие, обратное умножению, то легко вывести следующее правило: для выполнения деления двух комплексных чисел, заданных в тригонометрической форме, следует их модули разделитьу а аргументы вычесть:

Возможно вам будут полезны данные страницы:

Пример 2.

Найти частное от деления числа на число

Решение:

Находим по формуле (17.2):

Используем теперь равенство (17,1) для возведения произвольного комплексного числа в натуральную степень Для этого придется модуль этого числа взять множителем раз и аргумент взять слагаемым раз. Это приводит к равенству

Равенство (17.3) называется формулой Муавра. Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень у а аргумент умножить на показатель степени.

Пример 3.

Вычислить

Решение:

В соответствии с формулой Муавра (17.3)

Если число задано в алгебраической форме то для возведения его в степень с помощью формулы Муавра надо предварительно записать его в тригонометрической форме.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

где $\left| z \right|$ — модуль комплексного числа, $\text< >\!\!\varphi\!\!\text< >$ — некоторый угол, который называется аргумент комплексного числа (пишут $\text< >\!\!\varphi\!\!\text< >=\arg \left( z \right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=\sqrt<3>+i$.

Переписываем исходное число в виде $z=\sqrt<3>+1\cdot i$ и считаем модуль:

Выносим модуль за скобки:

\[z=\sqrt<3>+1\cdot i=2\cdot \left( \frac<\sqrt<3>><2>+\frac<1><2>\cdot i \right)\]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $\frac<\text< >\!\!\pi\!\!\text< >><6>$ с тем же успехом можно взять аргумент $\frac<13\text< >\!\!\pi\!\!\text< >><6>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

\[\begin & <_<1>>=\left| <_<1>> \right|\cdot \left( \cos \alpha +i\sin \alpha \right) \\ & <_<2>>=\left| <_<2>> \right|\cdot \left( \cos \beta +i\sin \beta \right) \\ \end\]

Тогда их произведение равно

\[<_<1>>\cdot <_<2>>=\left| <_<1>> \right|\cdot \left| <_<2>> \right|\cdot \left( \cos \left( \alpha +\beta \right)+i\sin \left( \alpha +\beta \right) \right)\]

А если ещё и $\left| <_<2>> \right|\ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

\[\begin <_<1>>\cdot <_<2>> & =2\cdot 5\cdot \left( \cos \left( \frac<\pi ><3>+\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>+\frac<\pi > <6>\right) \right)= \\ & =10\cdot \left( \cos \frac<\pi ><2>+i\sin \frac<\pi > <2>\right) \\ \end\]

\[\begin \frac<<_<1>>><<_<2>>> & =\frac<2><5>\cdot \left( \cos \left( \frac<\pi ><3>-\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>-\frac<\pi > <6>\right) \right)= \\ & =0,4\cdot \left( \cos \frac<\pi ><6>+i\sin \frac<\pi > <6>\right) \\ \end\]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

Возведём его в квадрат, умножив на само себя:

\[\begin <^<2>> & =z\cdot z = \\ & =\left| z \right|\left| z \right|\cdot \left( \cos \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right)+i\sin \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right) \right)= \\ & =<<\left| z \right|>^<2>>\cdot \left( \cos 2\text< >\!\!\varphi\!\!\text< >+i\sin 2\text< >\!\!\varphi\!\!\text < >\right) \\ \end\]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

в степень $n\in \mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

\[\begin \sqrt<3>-i & = 2\cdot \left( \frac<\sqrt<3>><2>+i\cdot \left( -\frac<1> <2>\right) \right)= \\ & =2\cdot \left( \cos \left( -\frac<\pi > <6>\right)+i\sin \left( -\frac<\pi > <6>\right) \right) \\ \end\]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

4. Дополнение 1. Геометрический подход

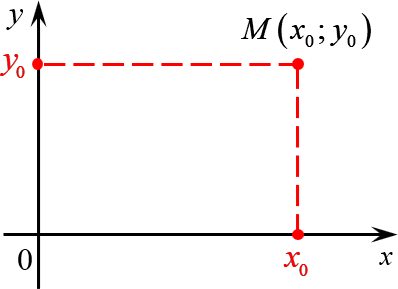
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

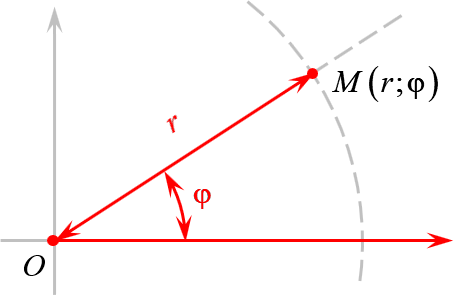
А есть полярная система координат, где точки задаются поворотом на угол $\varphi $ и расстоянием до центра $r$:

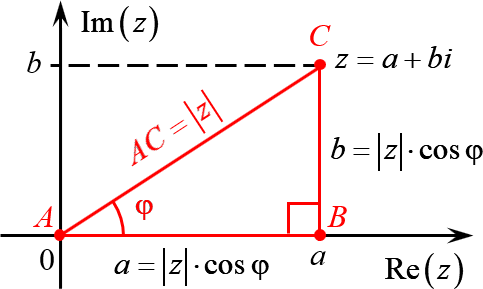
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $\angle BAC=\varphi $. Тогда:

\[\begin & AB=AC\cdot \cos \varphi =\left| z \right|\cdot \cos \varphi \\ & BC=AC\cdot \sin \varphi =\left| z \right|\cdot \sin \varphi \\ \end\]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

\[\begin a+bi & =\left| z \right|\cos \varphi +i\cdot \left| z \right|\sin \varphi = \\ & =\left| z \right|\left( \cos \varphi +i\sin \varphi \right) \\ \end\]

Итак, мы перешли от пары $\left( a;b \right)$ к паре $\left( \left| z \right|;\varphi \right)$, где $\left| z \right|$ — модуль комплексного числа, $\varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $\varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $\varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

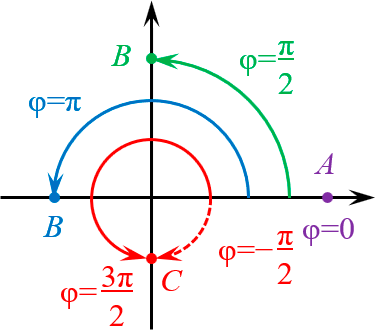
5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $\varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $\varphi =\pi $ (синяя точка $B$).
• На положительной полуоси ординат $\varphi =\frac<\pi ><2>$ (зелёная точка $B$).
• На отрицательной — $\varphi =\frac<3\pi ><2>$ (красная точка $C$). Однако ничто не мешает рассмотреть $\varphi =-\frac<\pi ><2>$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $a\ne 0$ и $b\ne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<<\varphi >_<1>>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $A\left( 3;4 \right)$ удалена от начала координат на расстояние 5:

\[\begin 3+4i & =5\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\operatorname\frac<4> <3>\end\]

Для точки $B\left( 6;-6 \right)$ арктангенс оказался табличным:

\[6-6i=6\sqrt<2>\cdot \left( \cos \left( -\frac<\pi > <4>\right)+i\sin \left( -\frac<\pi > <4>\right) \right)\]

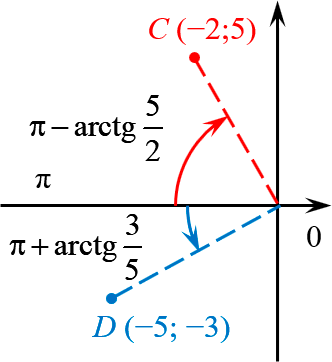
В левой полуплоскости откладываем от луча, соответствующего углу $\pi $:

Итого для точки $C\left( -2;5 \right)$ имеем:

\[\begin -2+5i & =\sqrt<29>\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi -\operatorname\frac<5> <2>\end\]

И, наконец, для точки $D\left( -5;-3 \right)$:

\[\begin -5-3i & =\sqrt<34>\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi +\operatorname\frac<3> <5>\end\]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =\sqrt[<3>] <8>\cdot \left(\cos \frac<2k\pi > <3>+i\cdot \sin \frac<2k\pi > <3>\right),\, \, \, k=0. 2$.

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <8>\cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[<3>] <8>=2$.

При $k=1$ получаем

\[x_ <1>=\sqrt[<3>] <8>\cdot \left(\cos \frac<2\pi > <3>+i\cdot \sin \frac<2\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=-1+\sqrt <3>\cdot i.\]

При $k=2$ получаем

\[x_ <2>=\sqrt[<3>] <8>\cdot \left(\cos \frac<4\pi > <3>+i\cdot \sin \frac<4\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=-1-\sqrt <3>\cdot i.\]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

\[\varphi =\arg z=arctg\frac<1> <1>=arctg1=\frac<\pi > <4>\]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi /4> <3>+i\cdot \sin \frac<\pi /4> <3>\right)=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)=\sqrt[<6>] <2>\cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

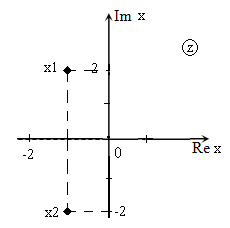
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

\[D=2^ <2>-4\cdot 1\cdot 5=4-20=-16.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $\overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1\pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

\[x^ <2>-(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\] \[x^ <2>-x+2i\cdot x-x-2i\cdot x+1-4i^ <2>=0\] \[x^ <2>-2x+1+4=0\] \[x^ <2>-2x+5=0\]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!