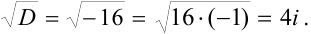Решение квадратных комплексных уравнений с отрицательным дискриминантом

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 253. Извлечение корней квадратных из отрицательных чисел.
Решение квадратных уравнений с отрицательными дискриминантами

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: — b 2 = — 1, b = ± 1.

Следовательно, комплексными числами, квадраты которых равны —1, являются только числа i и —i, Условно это записывается в виде:

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а. Такими числами являются √ a i и —√ a i . Условно это записывается так:

Под √ a здесь подразумевается арифметический, то есть положительный, корень. Например, √ 4 = 2, √ 9 =.3; поэтому

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда

Итак, данное уравнение имеет два корня: х₁ = — 1 +2i, х₂ = — 1 — 2i. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

2022. (У с т н о.) Решить уравнения:

2023. Найти все комплексные числа, квадраты которых равны:

2024. Решить квадратные уравнения:

Решить системы уравнений (№ 2025, 2026):

2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными.

2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются:

2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i) (2i — 4).

2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 — i
1— 3i .

Решение квадратных уравнений с отрицательным дискриминантом

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример №42.4.

Решить уравнение: .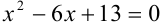

Решение:

Найдем дискриминант: .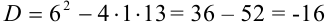

Тогда .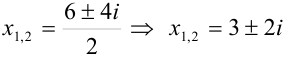

Ответ: .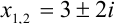

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение -й степени имеет комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Инструкция к практической работе № 1 по теме «Комплексные числа»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Министерство образования Оренбургской области

Государственное автономное профессиональное образовательное учреждение

«Орский машиностроительный колледж» г. Орска Оренбургской области

К ПРАКТИЧЕСКОЙ РАБОТЕ №1

ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

Преподаватель: О.В. Марченко

Практическая работа № 1

Тема: «Комплексные числа»

Цель: научиться осуществлять действия над комплексными числами в алгебраической форме, изображать комплексные числа на плоскости, решать квадратные уравнения с отрицательным дискриминантом.

1) Ознакомьтесь с теорией по теме:

Мнимой единицей называется число , обладающее свойством .

Числа вида a + bi , где a и b – действительные числа, – мнимая единица, называют комплексными. Число a называют действительной частью комплексного числа, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части.

Запись комплексного числа в виде z = a + bi называется алгебраической формой комплексного числа.

Любое комплексное число z = a + bi можно изобразить на комплексной плоскости в виде вектора с началом в точке О (0,0) и концом в точке М (а; b ) .

Пример1. Построить геометрическую модель комплексного числа .

Два комплексных числа называют сопряженными, если они отличаются друг от друга только знаком перед мнимой частью. Сопряженные комплексные числа обозначают: и . Например, и ;

Действия над комплексными числами, заданными в алгебраической форме

Пусть даны комплексные числа: и .

Сложение .

Вычитание

Умножение

Возведение в степень производят по правилу возведения двучлена в соответствующую степень.

При делении двух комплексных чисел в алгебраической форме, необходимо умножить делимое и делитель на комплексное число, сопряженное делителю.

;

, так как , , то получим

Решение квадратных уравнений с отрицательным дискриминантом

Квадратное уравнение , для которого дискриминант отрицателен, в множестве R действительных чисел не имеет решения, так как корень из отрицательного числа в этом множестве не имеет действительного значения. Рассмотрим решение этого уравнения в множестве С комплексных чисел.