Разработка уроков по теме «Комплексные числа» 10 класс
план-конспект урока по алгебре (10 класс) по теме
Знакомство с комплексными числами и основными операциями над ними.
Скачать:
| Вложение | Размер |
|---|---|
| Комплексные числа | 170.5 КБ |
Предварительный просмотр:
НОУ – лицей «Армавирский классический лицей»
Армавир 2015 год
Алгебра и начала анализа (8 часов)
- Комплексные числа в алгебраической форме и арифметические операции над ними (2 часа).
- Тригонометрическая форма записи комплексного числа(2 часа).
- Решение квадратных уравнений с отрицательным дискриминантом и комплексными коэффициентами(1 час).
- Возведение комплексного числа в степень. Извлечение квадратного корня из комплексного числа (2 часа).
- Контрольная работа (1 час).
Практикум по алгебре и началам анализа
- Арифметические операции над комплексными числами, записанными в алгебраической форме(1 час).
- Решение квадратных уравнений с отрицательным дискриминантом и комплексными коэффициентами(2 час).
- Возведение комплексного числа в степень. Извлечение квадратного корня из комплексного числа (1 час).
Тема: «Комплексные числа в алгебраической форме и арифметические операции над ними».
- формирование понятия «комплексные числа»;
- формирование навыков и умений выполнения арифметических операций над комплексными числами;
- развитие мышления;
- воспитание внимания и сосредоточенности.
- Организационный момент (3 мин).
- Фронтальный опрос, подводящий к изучению новой темы (15мин).
- Обьяснение нового материала (35 мин).
- Практическая часть (20 мин).
- Постановка домашнего задания (3 мин).
- Подведение итогов урока.(4 мин).
Учитель проверяет готовность класса к уроку. Далее сообщается, что сегодня на уроке начинается изучение новой темы «Комплексные числа». Учащимся предлагается записать в тетради дату и тему урока.
Посредством фронтального опроса осуществляется активизация знаний по ранее изученному материалу.
- Какие виды чисел вы уже знаете? (Натуральные; Целые; Рациональные; Иррациональные).
- Какие числа мы называем натуральными? ( Натуральные, т.е. числа, употребляемые при счете – 1,2,3,…)
- Какие числа мы называем целыми? (Целые – натуральные и им противоположные).
- Какие числа мы называем рациональными? (Рациональные – целые и дробные числа (положительные и отрицательные).
- Какие числа мы называем иррациональными? (Иррациональные – числа, которые нельзя представить в виде дроби m/n, где m – целое, n — натуральное).
Сегодня мы познакомимся еще с одним видом чисел – комплексными числами.
- Обьяснение нового материала.
Рассмотрим квадратное уравнение
Применив к нему правило нахождения корней квадратного уравнения, получим выражение:
которые можно записать в виде
x 1,2=1 ± 3 i (i= — 1).
Мы не получим действительного решения, т.к. – 3 не есть действительное число. Выражения вида вида (2) называют комплексными числами.
Опр.1: Комплексным числом называется выражение
где a и b – действительные числа, а i – специальный знак, при этом:
- i’ = -1 (4)
- a + 0i = a (5)
- 0 + bi = bi (6)
- a + bi = c + di, где a, b, c, d – действительные числа, причем a = c и b = d.
Опр.2: Число 0 + bi = bi называется мнимым или чисто мнимым.
Любое действительное число a – частный случай комплексного числа. На основании (2) его можно записать в виде a=a+0i.
Например: 0=0+0i, но если a+bi=0 , то a+bi=0+0i => a=b=0.
Т.о. комплексное число a+bi=0 ⬄ a=0 и b=0.’
Арифметические действия над комплексными числами.
- Сложение — (a+bi)+(c+di)=(a+c)+(b+d)i
- Разность — (a+bi)-(c+di)=(a-c)+(b-d)i
- Произведение — (a+bi) · (c+di)=ac+bci+adi-bd=(ac-bd)+(bc+ad)i
- Частное —
Замечание: из (4) следует:
i = i, i=-i, i = i i =1,
i =I, i =i, i =i i =-1,…
Примеры: Привести к виду a+bi , где a и b – действительные числа следующие комплексные числа:
Комплексные числа нередко обозначают одной буквой. Пишут:
и говорят: задано комплексное число z.
Опр.3: Число a называют действительной частью z и обозначают:
Re z=a (реальный, действительный)
Число b – мнимой частью и обозначают:
Im z=b(мнимый, воображаемый).
Опр.4: Если z=a+bi есть комплексное число ( a, b – действительные числа), то a-bi называют ему сопряженным числом и пишут z=a-bi .
Если b=0 , то z=z. Числа z и z взаимно сопряжены друг к другу.
Даны комплексные числа
- z1=1 — i и z2=4i — 2
- z1=1 + i и z2=-6 + 4i
- сумму z = z1+ z2 и укажите Re z, Im z.
- разность z = z1 — z2 и укажите комплексное число, которое сопряжено с z.
- произведение z = z1 · z2.
- частное z = z1/ z2
- Постановка домашнего задания.
Даны комплексные числа
- z1=15 -5 i и z2=1 + 2i
- z1=5 +10 i и z2=2 — i
- сумму z = z1+ z2 и укажите Re z, Im z.
- разность z = z1 — z2 и укажите комплексное число, которое сопряжено с z.
- произведение z = z1 · z2.
- частное z = z1/ z2
Итоги урока подводятся оценкой ответов учеников.
Тема: «Тригонометрическая форма записи комплексного числа».
- формирование понятий «модуль комплексного числа», «аргумент числа z », «запись комплексных чисел в тригонометрической форме;
- формирование навыков и умений выполнения преобразования комплексных чисел, записанных в алгебраической форме, в тригонометрическую форму;
- развитие логического мышления;
- воспитание внимания, сосредоточенности и усидчивости.
- Организационный момент (2 мин).
- Входной контроль (опрос) (5 мин).
- Самостоятельная работа (10 мин).
- Обьяснение нового материала (40 мин).
- Практическая часть (20 мин).
- Постановка домашнего задания (2 мин).
- Подведение итогов урока.(2 мин).
Учитель проверяет готовность класса к уроку. Далее сообщается, что сегодня на уроке продолжается изучение темы «Комплексные числа», в частности будут изучены комплексные числа, записанные в тригонометрической форме. Учащимся предлагается записать в тетради дату и тему урока.
Учащиеся отвечают на следующие вопросы:
- Дайте определение комплексных чисел.
( Комплексным числом называется выражение a+bi, где a и b – действительные числа, а i – специальный знак, при этом:
- i’ = -1
- a + 0i = a
- 0 + bi = bi
- a + bi = c + di, где a, b, c, d – действительные числа, причем a = c и b = d.)
- Какое число мы называем мнимой частью комплексного числа?
( Число 0 + bi = bi называется мнимым или чисто мнимым.)
- В каком случае мы можем сказать, что комплексное число a+bi равно нулю?
( Комплексное число a+bi=0 ⬄ a=0 и b=0.)
- Что такое действительная и мнимая часть числа z ?
(Число a называют действительной частью z и обозначают:
Re z=a (реальный, действительный)
Число b – мнимой частью и обозначают:
Im z=b(мнимый, воображаемый).
- Какое число мы называем сопряженным комплексному числу?
(Если z=a+bi есть комплексное число ( a, b – действительные числа), то a-bi называют ему сопряженным числом и пишут z=a-bi. Если b=0 , то z=z. Числа z и z взаимно сопряжены друг к другу.)
Даны комплексные числа
- сумму z = z1+ z2 и укажите Re z, Im z.
- разность z = z1 — z2 и укажите комплексное число, которое сопряжено с z.
- произведение z = z1 · z2.
- частное z = z1/ z2
Даны комплексные числа:
- сумму z = z1+ z2 и укажите Re z, Im z.
- разность z = z1 — z2 и укажите комплексное число, которое сопряжено с z.
- произведение z = z1 · z2.
- частное z = z1/ z2
Даны комплексные числа
- сумму z = z1+ z2 и укажите Re z, Im z.
- разность z = z1 — z2 и укажите комплексное число, которое сопряжено с z.
- произведение z = z1 · z2.
- частное z = z1/ z2
- Обьяснение нового материала.
Рассмотрим прямоугольную систему координат xOy. Комплексное число z=x+yi изображается на плоскости точкой z(x,y).
Имеет место взаимно однозначное соответствие между точками плоскости и комплексными числами, т.е. каждому действительному числу соответствует точка плоскости; двум разным комплексным числам соответствуют разные точки, и каждая точка соответствует некоторому комплексному числу.
В силу этого соответствия координатную плоскость называют еще комплексной плоскостью.
Опр.1: Введем вектор с началом в нулевой точке О и концом в А . Его длина
называется модулем комплексного числа z. Угол ϕ, образуемый вектором ОА с положительной полуосью x (отсчитываемый против часовой стрелки), называется аргументом числа z.
Опр.2: Каждое комплексное число z=x+yi имеет свой модуль ρ=׀z׀ и аргумент ϕ= Arg z.
Но аргумент определяется не однозначно. Если ϕ есть аргумент z, то ϕ +2kπ, где k=0, ± 1,±2,…тоже аргумент z, поэтому аргумент z должен удовлетворять неравенству 0≤ ϕ 2kπ.
Опр.2: Аргумент z обозначают Arg z и называют главным значением аргумента z или аргументом z в приведенном виде . Любое значение аргумента z определяется по формуле:
Arg z = arg z + 2kπ,
где k одно из чисел k=0, ± 1,±2,…
x = ρ cos ϕ, y = = ρ sin ϕ ,
z = x + iy = = ρ (cos ϕ + i sin ϕ ).
— Тригонометрическая форма записи комплексного числа.
- Найдите модуль и аргумент комплексного числа:
а) z = 4 + 4i; б) z = 3 — 3i;
в) z = — √ 3 /2 -½i ; г) z = ½ + √ 3 /2 i;
д) z = (1-2i)²; е) z = (2+i)².
- Представьте данное комплексное число
a) в алгебраической форме:
z = 2 (cos π/4 + i sin π/4); z = 4 (cos π/3 + i sin π/3);
б) в тригонометрической форме:
z = 1 + √ 3i; z = 2 + 2i.
а) 3 ( cos π/2 + i sin π/2) · ( cos π/6 + i sin π/6);
б) √ 3 ( cos π/3 + i sin π/3) · √ 12 ( cos π/6 + i sin π/6);
в) [18 (cos 47º + i sin 47º)]:[9 (cos 17º + i sin 17º)];
г) [20 (cos 72º + i sin 72º)]:[5 (cos 12º + isin 12º)]
- Постановка домашнего задания.
Конспект, решение следующих заданий:
- Найдите модуль и аргумент комплексного числа:
а) z = 3 + 3i; б) z = 5 — 5i;
в) z = √ 2 /2 -½i ; г) z = ½ — √ 2 /2 i;
д) z = (4-3i)²; е) z = (1+2i)².
- Представьте данное комплексное число
a) в алгебраической форме:
z = 2(cos π + i sin π); z = 2 (cos π/6 + i sin π/6);
б) в тригонометрической форме:
z =- 1 — √ 3i; z = 1 — i.
а) ( cos π/4 + i sin π/4) · 2 ( cos π/6 + i sin π/6);
б) √ 6 ( cos π/3 + i sin π/3) · √ 3 ( cos π/6 + i sin π/6);
в) [16cos 56º + i sin 56º)]:[8 (cos 4º + i sin 4º)];
г) [12 (cos 75º + i sin 75º)]:[3(cos 15º + isin 15º)
Итоги урока подводятся оценкой ответов учащихся.
Тема: «Решение квадратных уравнений с отрицательным дискриминантом. Возведение комплексного числа в степень».
- формирование навыков и умений решения квадратных уравнений с отрицательным дискриминантом и комплексными коэффициентами;
- формирование навыков и умений возведения комплексного числа в степень;
- развитие логического мышления;
- воспитание внимания, сосредоточенности и усидчивости.
- Организационный момент (3 мин).
- Самостоятельная работа (20 мин).
- Обьяснение нового материала (25 мин).
- Практическая часть (25мин).
- Постановка домашнего задания (4 мин).
- Подведение итогов урока.(3 мин).
Учитель проверяет готовность класса к уроку. Далее сообщается, что сегодня на уроке будет рассмотрено решение квадратных уравнений с отрицательным дискриминантом, а также возведение комплексного числа в степень . Учащимся предлагается записать в тетради дату и тему урока.
2. 3 ( cos π/4 + i sin π/4) · 2 ( cos π/6 + i sin π/6).
2) Тригонометрическая форма записи комплексного числа (формула).
2. 12(cosπ+i sin π) · ( cos π/6 + i sin π/6).
2) Главный аргумент комплексного числа z и его модуль (формулы).
2. 6(cos2π + i sin2π) · 2 ( cos π/3 + i sin π/3).
2 ) Определение комплексного числа .
- Обьяснение нового материала.
Решение квадратных уравнений с отрицательным дискриминантом.
Рассмотрим квадратное уравнение в общем виде:
где p, q – действительные числа.
— Если ( D=b’-4ac)>0 , то уравнение (1) имеет 2 действительных корня
— Если D=0 , то уравнение (1) имеет 1 действительный корень
— Если D , то уравнение (1) имеет 2 комплексных корня
Например: Решить в комплексных числах квадратнoе уравнения:
D= 1-4*1*1=-3, D , значит уравнение имеет 2 комплексных корня, причем D= √ 3i .
X1,2= (-1± √ 3i )/2, т.е. x1= -1/2+ √ 3i/2, x2=-1/2- √ 3i/2.
Ответ: x=-1/2± √ 3i /2.
Возведение комплексного числа в степень.
Пусть комплексноек число z задано в тригонометрической форме, т.е. z=ρ(cosϕ+i sinϕ ) , а n — степень, в которую возводится данное комплексное число, тогда имеет место следующее правило.
Правило : При возведении комплексного числа в степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени, т.е.
(ρ(cosϕ+i sinϕ ))’= ρ’(cos nϕ+i sin nϕ ).
Например: Записать в алгебраической форме комплексные числа:
( √ 3+i)^3; ρ=2; z=(2( √ 3/2+1/2i))^3=(2(cosπ/6+i sinπ/6))^3=2^3(cos3π/6+i sin3π/6)=8(cosπ/2+i sinπ/2)=8(0+i)=8i.
- Решить уравнения:
|
|
- Записать в алгебраической форме комплексные числа:
|
|
- Постановка домашнего задания.
- Решить уравнения:
6.Подведение итогов урока. Итоги урока подводятся оценкой ответов учащихся. Тема: «Извлечение квадратного корня из комплексного числа».
Учитель проверяет готовность класса к уроку. Далее сообщается, что сегодня на уроке будет изучено правило извлечения квадратного корня из комплексного числа. Учащимся предлагается записать в тетради дату и тему урока. Для проверки домашнего задания к доске вызываются 4 ученика. Пока они записывают решение домашнего задания на доске, остальные учащиеся отвечают на следующие вопросы:
Опр.1: Любое комплексное чило x, удовлетворяющее уравнению x’=c , называют корнем квадратным из числа c и обозначают символом √ c, причем x’=c ⇔ x=ρ(cos ϕ +i sin ϕ) и c=r(cos α + i sin α) ρ’(cos2 ϕ +i sin2 ϕ) =r(cos α + i sin α) Например: Решить в комплексных числах уравнения: Решить в комплексных числах уравнения:
Решить в комплексных числах уравнения: Итоги урока подводятся оценкой ответов учащихся. Тема: «Контрольная работа №4 по теме «Комплексные числа».
Учитель проверяет готовность класса к уроку. Далее сообщается, что сегодня на уроке будут проведена контрольная работа по теме «Комплексные числа». Учащимся предлагается записать в тетради дату и тему контрольной работы.
а) (7+3i)(7-3i)+2; б) √ 2 ( cos π/4 + i sin π/4) · 2 ( cos π/2 + i sin π/2).
|






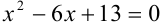 .
.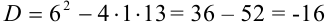 .
.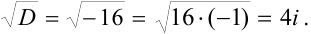
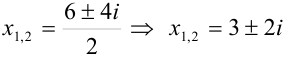 .
.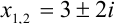 .
. -й степени имеет
-й степени имеет 

