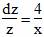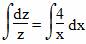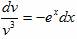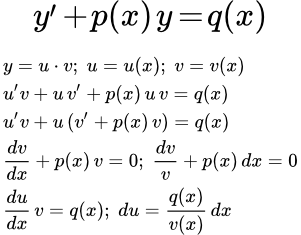Решение линейных дифференциальных уравнений первого порядка методом бернулли

Уравнения Бернулли

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений Бернулли.

• Решение онлайн
• Видеоинструкция

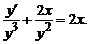
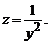
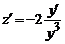
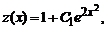
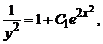
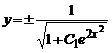
Пример 1 . Найти общее решение уравнения y’ + 2xy = 2xy 3 . Это уравнение Бернулли при n=3. Разделив обе части уравнения на y 3 получаем Делаем замену Тогда и поэтому уравнение переписывается в виде -z’ + 4xz = 4x. Решая это уравнение методом вариации произвольной постоянной, получаем откуда или, что то же самое, .

Пример 2 . y’+y+y 2 =0
y’+y = -y 2

Разделим на y 2
y’/y 2 + 1/y = -1

Делаем замену:
z=1/y n-1 , т.е. z = 1/y 2-1 = 1/y
z = 1/y
z’= -y’/y 2

Получаем: -z’ + z = -1 или z’ — z = 1

Далее надо найти z и выразить через него y = 1/z .

Пример 3 . xy’+2y+x 5 y 3 e x =0
Решение.
а) Решение через уравнение Бернулли.
Представим в виде: xy’+2y=-x 5 y 3 e x . Это уравнение Бернулли при n=3 . Разделив обе части уравнения на y 3 получаем: xy’/y 3 +2/y 2 =-x 5 e x . Делаем замену: z=1/y 2 . Тогда z’=-2/y 3 и поэтому уравнение переписывается в виде: -xz’/2+2z=-x 5 e x . Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение: -xz’/2+2z=0
1. Решая его, получаем: z’=4z/x

Интегрируя, получаем:
ln(z) = 4ln(z)
z=x 4 . Ищем теперь решение исходного уравнения в виде: y(x) = C(x)x 4 , y'(x) = C(x)’x 4 + C(x)(x 4 )’
-x/2(4C(x) x 3 +C(x)’ x 4 )+2y=-x 5 e x
-C(x)’ x 5 /2 = -x 5 e x или C(x)’ = 2e x . Интегрируя, получаем: C(x) = ∫2e x dx = 2e x +C
Из условия y(x)=C(x)y, получаем: y(x) = C(x)y = x 4 (C+2e x ) или y = Cx 4 +2x 4 e x . Поскольку z=1/y 2 , то получим: 1/y 2 = Cx 4 +2x 4 e x

б) решение через замену переменных
y=uv
x(u’v + uv’)+2uv+x 5 u 3 v 3 e x =0
v(x u’ + 2u) + xuv’+ x 5 u 3 v 3 e x = 0
a) xu’+2u = 0
или ln(u)=ln(x -2 ). Откуда u = x -2
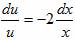
b) xuv’+ x 5 u 3 v 3 e x = 0
x x -2 v’+ x 5 x -6 v 3 e x = 0
v’/x+ v 3 e x /x = 0
v’+ v 3 e x = 0

или 1/y 2 = Cx 4 +2x 4 e x

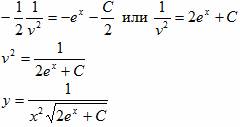
Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:

Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Бернулли.

Метод введения двух функций (Бернулли)

Ищем решение исходного уравнения в виде произведения двух функций:
y = u · v
где u, v — функции от x . Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:

Выносим u за скобки:
(1)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(2)
Это уравнение с разделяющимися переменными.

Разделяем переменные. Умножаем обе части уравнения на dx и делим на v

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение.

Потенцируем и опускаем знак модуля (Знак модуля сводится к умножению на постоянную ±1 ).

Подставим в (1) учитывая, что согласно (2), выражение в скобках равно нулю:

Отсюда

Интегрируем

Окончательно находим:

.

Пример решения линейного дифференциального уравнения первого порядка методом Бернулли

Делаем подстановку:
y = u · v
где u, v — функции от x . Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:

Выносим u за скобки:
(3)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Это уравнение с разделяющимися переменными,
.
Разделяем переменные. Умножаем обе части уравнения на dx и делим на xv :

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. По таблице интегралов, находим:

Или

Потенцируем и опускаем знаки модуля (Знак модуля сводится к умножению на постоянную ±1 ).

Подставим в (3) учитывая, что согласно (4), выражение в скобках равно нулю:

Отсюда

Интегрируем, применяя формулу :
.
Окончательно находим:
.

Общее решение уравнения:

Автор: Олег Одинцов . Опубликовано: 24-07-2012 Изменено: 27-02-2015

Линейные дифференциальные уравнения 1-го порядка
и уравнение Бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид

где и — заданные функции от , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если , то уравнение (1) называется линейным однородным . Оно является уравнением с разделяющимися переменными и имеет общее решение

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной , который состоит в том, что решение уравнения (1) ищется в виде

Пример 1. Решить уравнение .

Решение. Применим метод вариации постоянной. Рассмотрим однородное уравнение , соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными. Его общее решение имеет вид .

Общее решение неоднородного уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем , откуда . Итак, общее решение неоднородного уравнения будет , где — постоянная интегрирования.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно как функция от . Нормальный вид такого уравнения

Пример 2. Решить уравнение .

Решение. Данное уравнение является линейным, если рассматривать как функцию от :

Применяем метод вариации произвольной постоянной. Сначала решаем соответствующее однородное уравнение

которое является уравнением с разделяющимися переменными. Его общее решение имеет вид .

Общее решение уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем

Отсюда, интегрируя по частям, будем иметь

Исходное уравнение может быть проинтегрировано также следующим образом. Полагаем

где и — неизвестные функции от , одна из которых, например , может быть выбрана произвольно.

Подставляя в , после преобразования получаем

Определяя из условия , найдем затем из функцию , а следовательно, и решение уравнения . В качестве можно взять любое частое решение уравнения .

Пример 3. Решить задачу Коши: .

Решение. Ищем общее решение уравнения в виде ; имеем . Подставляя выражение для и в исходное уравнение, будем иметь

Функцию находим из условия . Беря любое частное решение последнего уравнения, например , и подставляя его, получаем уравнение , из которого находим функцию . Следовательно, общее решение уравнения будет

Используя начальное условие , получаем для нахождения уравнение , откуда ; так что решением поставленной задачи Коши будет функция .

Пример 4. Известно, что между силой тока и электродвижущей силой в цепи, имеющей сопротивление и самоиндукцию , существует зависимость , где и — постоянные. Если считать функцией времени , то получим линейное неоднородное уравнение для силы тока :

Найти силу тока для случая, когда и .

Решение. Имеем . Общее решение этого уравнения имеем вид . Используя начальное условие (13), получаем из , так что искомое решение будет

Отсюда видно, что при сила тока стремится к постоянному значению .

Пример 5. Дано семейство интегральных кривых линейного неоднородного уравнения .

Показать, что касательные в соответственных точках к кривым , определяемым линейным уравнением, пересекаются в одной точке (рис. 13).

Решение. Рассмотрим касательную к какой-либо кривой в точке .Уравнение касательной в точке имеет вид

По определению, в соответственных точках является постоянным, а переменным. Беря любые две касательные к линиям в соответственных точках, для координат точки их пересечения, получаем

Отсюда видно, что все касательные к кривым в соответственных точках ( фиксировано) пересекаются в одной и той же точке

Исключая в системе аргумент , получаем уравнение геометрического места точек .

Пример 6. Найти решение уравнения , удовлетворяющее условию: ограничено при .

Решение. Общее решение данного уравнения . Любое решение уравнения, получаемое из общего решения при , будет неограниченно, так как при функция ограничена, а . Отсюда следует, что данное уравнение имеет единственное решение , ограниченное при , которое получается из общего решения при .

Уравнение Бернулли

Дифференциальное уравнение Бернулли имеет вид

С помощью замены переменной уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.

Пример 7. Решить уравнение Бернулли .

Решение. Делим обе части уравнения на :

Делаем замену переменной , откуда . После подстановки последнее уравнение обратится в линейное уравнение

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как и линейное уравнение, и с помощью подстановки .

Пример 8. Решить уравнение Бернулли .

Решение. Применим метод вариации произвольной постоянной. Общее решение соответствующего однородного уравнения имеет вид . Общее решение уравнения ищем в виде , где — новая неизвестная функция. Подставляя в исходное уравнение, будем иметь

Для нахождения функции получим уравнение с разделяющимися переменными, из которого, разделяя переменные и интегрируя, найдем

Итак, общее решение исходного уравнения .

Некоторые нелинейные уравнения первого порядка с помощью удачно найденной замены переменных сводятся к линейным уравнениям или к уравнениям Бернулли.

Пример 9. Решить уравнение .

Решение. Запишем данное уравнение в виде .

Деля обе части уравнения на , получаем .

Замена приводит это уравнение к линейному , общее решение которого .

Заменяя его выражением через , получаем общий интеграл данного уравнения .

В некоторых уравнениях искомая функция может находиться под знаком интеграла. В этих случаях иногда удается путем дифференцирования свести данное уравнение к дифференциальному.

Пример 10. Решить уравнение 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAUQAAABNBAMAAAAsvACJAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAUbAgWgQITGh8LHQkeBuUEPaAAAHI0lEQVRo3u1afWxTVRQ/97XvtbUbvG6OwJxrmcMpzHRjgBLULQRJEGTFMBMRWQMaiSBrMBJCjBtEQSdmi5sJEc0o4hAXQ8N3gnEDEwxfo3HxD8jIhMlfRnHdxjYm1HPfu+36um4QPCRN2E229vX1nv7u+fj9zr0twNh4AIcyxZfsEFfl/ZLsEF+DBckO8RBMpTZpca0ntTcD3CotQjYl/6KHGCK1F4OVa1xJDhGWA2lg6mEFOcSvFS9l4uTDZWKA1r6rMiVEmPTbEeqCPr/gV1qLG+8Dk7Ex1U7C4Uh6k9bOWmqE1s4CUnubXt5NDXHd3G9J7X35SC81xNI3ekhZbMDyCjXlNCnzKe1lhBhxpwNpxGFJv0Fez7Z+WnsVJ8ghZvpp7bnJKQdqaCmHdXioEbLyElp7F6rIvdhM2nODElbJvbifdmcudZM70XqTdtWPDsS69Cj//+5oLbM1MMINU3RWRnccRFlL9x33TIuxUmXSkkgSKOSiBJW0PSF+C846Fbmw3xp2mqAJtwj/tNl3yJOcuBU6QzEXC/ENT4CjXjgM035LvIGTCeXkIFp9KXKVLcTlzQj+RrTlgbQW/fK9AVBGYRE29fLVOFrsi4nzd/iHLqgWnurwQmecAbkldomy/mD+k4e2MlIklaHodF1skIPsu4BdE9nfC7auUXqG3bDMZ+SwGCUwt+j6mqLzGjsH1viOJduw/nSB18Eh2oQGMLcA0CrucuzOALAV+rW5D8YNU7TPoqhsu8AZNNxriFECDi0VvWrWLaBD5VC8cPgSQWQcohxZbOmVyHR9LMabbk90rukKVAaHEcvsiOFxhZCOBt6ZIc8Qxq/r7/70GKS5KlxgXtxTAhLvLJS2L0LmRT3z44RD5bNXPifKKxbiRNE8sGKt3NIWDM5V2lzwEcwBWFpc74NMj1aDNbW5DfURckdbevVIRZNFcSDELlCeyfrD7RLMrUVOmTUH3euugpXuAy6wcN9VLym/Ibmn87etz+Ejj7+xTgXlWNbpak+cF/k/USUsrOWJdVooz5bbBT+pewC2nMnxQjpmgvLzW/s9W4pzRJoikogtS52O0V3Imy97lcnfrOueFNYezZMHmduDLmI8IvzDlCZ46ATUaNNz5/Exlz8twmRxmRobXMMDzUTeWsP6zawT8KR9F2vir7NB7nPMKXsjdPhYZ6Tm0NYNYQssXy3RIBaAKYSF6KxdLSpE1z8Zk67DV4rPO3z6h9lCUBGE8hgB550vQ4gSZAb4bHnevMWI3BuFuEeUeVhPK5yeV1Er9fIFS9zDpkIEEGTPq5aeIUrILlgdORewtLuiEJmWvTrNCiWw+1mryhOtVfgj088wF5rjWJRDdAjfZowAMVXXPz4dyl3mfg7R3C8gNrjYgKEIK4e6ImURh1ih5SIWXaR+skXZZQaUAX4WqnA95BArC5HX2DfazQ8NgQbhW4eaONDp3UO02Kya/Px1k18PNCtWOS3GNPrl0a4IA839mVkIWX5YU3JGFdadvZHFICFiuaT1WgJauVSUsHOTNvYoLcZyaVPBFmxWs9QEuShMZepQWSuqchGMD3DvOgPpWC7Ijc8iq5Vlt9iqZM1JMbYsdTpYJHlnLbh3dMMLQlwEU1SUmPrA6cIYmKpAQm4cF7QNrpVCtrjWD3PBfeQ2LI2j7n8dWCYho7h0o9b/COUeOI4QS3BGJsb0ElT/c9QZfB3cjdrHz/pe2JLqJus5KYUAU2Rd+/ttQkDKhRLIP7RegfQSmNCEImxG6rT+NfPSAeXs4TiKRaVY255fFzRANIfDWMWyMOUWYby00wvVO69XcVWxncYZNZgfq45/vi+Yuq8WNmkLSWnP3xnUqTvqi2Vl/JxgM9ssrjsi4rIS81bmAuhVIYXPmqhafCB5EwjgZtgaL4AO9KItYBAXsCAiR16rLoDb8AVNADfAau2KaamNtjZoj58MqZalzCjRxbo/LE3wohcm7B0S1RGGbNg5ZRi2ksIPzUMdZUoXZxubiNg1g6XCEVsdI4swQbNSr8wPdsSXRPWjdHMnR7QW+YbpwlCn4Sz4oFZvxvhn/G4Q5eDdnpYImlUOnvVpZK+p66lRZmwfqSW3njKuWm+KZ/KHV/WW1rCPs3nvdudyW431h/L0nTcGI2277SI7pNj9mn7OKGugj93btuDhAfLNlZxgv/Z/tlt28nM7SO2htZfdTw7RFCI+c/KTQ3R2PWhnTlBKfubERZl0FHvJITbQHmOJfpDU5N+k5rZJ5JzzsYWUc6w3J1EXNAtn7CU9Wrz1tosa4r51tCe0y6+Rfym7/DniNav01UJPEWMjGYeS60t2iCmPT092iI+Jg22q8dShuipiiBdpfzulBKeOp+Zu4h/JKd6F5IFGiLTMOPN+QKT0otQSSqUWgzbaH2zK5w+VUXtxO/HPXrdayXk29fCspJeXjTA2kmX8B/XH3ORQKCpxAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />.

Решение. Дифференцируя обе части этого уравнения по , получаем

Дифференцируя еще раз по , будем иметь линейное однородное уравнение относительно

Разделяя переменные и интегрируя, найдем . Это решение, как легко проверить, удовлетворяет исходному уравнению.