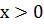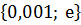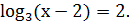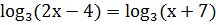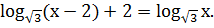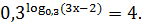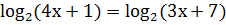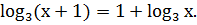Решение логарифмических неравенств.
Логарифмические неравенства в задании 14 профильного уровня ЕГЭ по математике встречаются чаще других. Это связано, в первую очередь, с тем, что выражения с логарифмом имеют ограниченную область допустимых значений, причём задаваемую также неравенством. Последнее обстоятельство приводит к тому, что решение логарифмического неравенства во многих случаях сводится к решению систем алгебраических неравенств (рациональных и не только).
В этом разделе рассмотрены типовые логарифмические неравенства – простейшие и соответствующие профильному уровню ЕГЭ. Все неравенства даны с решениями и комментариями, поэтому будут полезны и при текущем изучении или повторении этой темы.
Если возникают вопросы — обращайтесь через форму для письма, рисунок конверта кликабелен.
Узнайте, как можно поддержать сайт и помочь его развитию.
Основные положения и примеры решения простейших логарифмических неравенств.
С этим разделом могут ознакомиться и выпускники, которые планируют сдавать экзамен по математике на базовом уровне.
На профильном экзамене встречаются более сложные неравенства, но их также тем или иным образом требуется сводить к простейшим.
К простейшим относятся логарифмические неравенства, которые содержат неизвестную переменную в составе аргумента логарифмической функции с фиксированным основанием, т.е. это неравенства вида \(log_a
В более общих случаях неизвестная величина может встречаться и в основании логарифма.
Чтобы решать как логарифмические неравенства, так и логарифмические уравнения, нужно вспомнить определение и свойства логарифмической функции как таковой.
1) Логарифм – трансцендентная функция, т.е. аналитическая функция, которая не может быть задана с помощью алгебраического уравнения. Поэтому чтобы получить решение простейшего логарифмического неравенства, нужно сначала перейти к алгебраическим соотношениям, т.е. «убрать» логарифм.
2) Логарифм – однозначная и монотонная функция, что означает каждому значению аргумента из области определения соответствует единственное значение функции. Поэтому её можно сравнивать саму с собой и «вычёркивать» логарифм. Как и в каких случаях это делать, рассмотрим на примерых ниже.
3) Главное – логарифмическая функция имеет ограниченную область определения. Это означает, что при решении любых заданий с логарифмами, содержащими переменные, нужно не забывать про ОДЗ (область допустимых значений) этой переменной.
Область значений функции E = R – всё множество действительных чисел. Т.е. сам логарифм, в отличие от его аргумента и основания, может принимать любые значения из промежутка \((-\infty; +\infty)\).
Как уже упоминалось, логарифмическая функция монотонна. Посмотрите на её графики.
При a > 1 функция возрастающая,
Поэтому для решения простейших логарифмических неравенств достаточно преобразовать обе части неравенства к логарифму с одинаковым основанием и затем сравнить подлогарифмические выражения. Таким образом мы сравниваем функцию с самой собой при разных значениях её аргумента, т.е. как бы «вычёркиваем» log с обеих сторон неравенства. При этом,
— если основание степени больше единицы, то знак неравенства без «log» будет таким же, как знак исходного неравенства, что характерно для возрастающих функций – большему значению аргумента соответствует большее значение функции;
— если основание степени меньше единицы, то знак неравенства будет обратным по отношению к знаку исходного неравенства, что характерно для убывающих функций – большему значению аргумента соответствует меньшее значение функции.
Пример 1.
Решение.
Область допустимых значений (ОДЗ) выражения \(2x+7>0.\)
Воспользуемся определением логарифма, чтобы представить число −2 в виде значения логарифмической функции с основаением 0,2.
\[0,2^ <-2>= \left(\frac<1><5>\right)^ <-2>= \left(\frac<5><1>\right)^ <2>= 25,\]
следовательно \(-2 = \log_<0,2><25>,\) и заданное неравенство можно преобразовать к виду \[\log_<0,2><(2x+7)>\log_<0,2><25>.>\] Теперь можно «отбросить логарифм», изменив знак неравенства на противоположный, так как его основание 0,2 0,> \\ <2x+7 -3,5,>\\
Преобразуем неравенство:
\(\text
Таким образом, заданное неравенство равносильно системе неравенств \[\begin
Ответ: \(x \in (3; 8). \)
Введение вспомогательной переменной
Пример 4.
Решение.
Аргументом обоих логарифмов является один и тот же квадратный трёхчлен \(4+3x-x^2\), однако основания логарифмов различны – это 2 и 0,5, поэтому нужно воспользоваться свойствами логарифмической функции и привести логарифмы к одному основанию. Поскольку \(0,5 = \dfrac<1> <2>= 2^<-1>\), то приводить будем второй логарифм к основанию 2. Для этого используем формулу \(\log_\log_a\): \[\log_<0,5> <(4+3x-x^2)>= \log_<2^<-1>><(4+3x-x^2)>=\frac<1><-1>\log_2 <(4+3x-x^2)>= -\log_2<(4+3x-x^2)>\] Теперь неравенство имеет следующий вид \[\log_2^2 <(4+3x-x^2)>— 7\log_2 <(4+3x-x^2)>+10 > 0.\]
В последнем неравенстве неизвестная величина встречается в обоих слагаемых в совершенно одинаковой форме, поэтому можно продолжить решение методом введения вспомогательной переменной.
Пусть \(y = \log_2<(4+3x-x^2)>\), тогда логарифмическое неравенство преобразуется в обычное квадратное неравенство \[y^2 — 7y +10 > 0,\] которое решается графически (через параболу) или методом интервалов. Сделайте это самостоятельно. Ответ получится такой \(y \in (-\infty;2)\cup(5;+\infty)\) или, что то же самое \[\left[<\begin
Замечание 1. Чтобы не выписывать совокупности систем и системы совокупностей, особенно, если вы путаетесь в этих скобках, можно все этапы решения реализовать схемами на числовой оси.
Замечание 2. Заметим, что с некоторого момента решение задачи сводится к анализу неравенств, в которых один и тот же квадратный трёхчлен \(4+3x-x^2\) сравнивается с числовыми значениями. Поэтому дальнейшие действия можно свести к построению одной параболы – эскиза графика функции \(y = 4+3x-x^2\) – и посмотреть как она соотносится с горизонтальными линиями \(y = 0, \; y = 4\; и\; y =32.\) (Вспомните аналогичное задание 2-й части ОГЭ за 9-ый класс.) На это не уйдёт много времени, т.к. коэффициенты трёхчлена целые числа, корни легко вычисляются по теореме Виета, а параболу достаточно построить только по характерным точкам.
Как быстро построить параболу можно посмотреть в видеоуроке на youtube-канале Mathematichka.
Ответ: \(x \in (-1;0) \cup (3;4).\)
Решение.
Выпишем ОДЗ неравенства.
Условие положительности всех аргументов логарифмической функции \[\begin
Условие неравенства нулю знаменателей всех дробей \[\begin
В этом примере в отличие от предыдущего, напротив, основания всех логарифмов одинаковы – логарифм по основанию 4, но отличаются аргументы. Используем свойства логарифмов, чтобы упростить выражения. \[\log_4 <(64x)>= \log_4<64>+\log_4
Учитывая, что до сих пор все преобразования, которые производились, были равносильными, можем утверждать, что выколов точки 3 и −3 из возможных значений переменной \(y\), мы обеспечили неравенство нулю общего знаменателя дроби, а значит и всех дробей, участвовавших в равносильных преобразованиях. Тем самым выполнена вторая часть ограничений ОДЗ неравенства.
Итак, неравенство для переменной \(y = \log_4
Ответ: \(x \in \left(0; \;\dfrac<1><64>\right) \cup \ <4\>\cup (64;\;+\infty)\).
О разложении на множители
\( \log_3
Решение II – вспомогательная переменная.
ОДЗ: \(x>0.\)
Приведём логарифмы к одному основанию, например, к основанию 3. \[\log_4
Решение III – через уравнение.
ОДЗ: \(x>0.\)
Заменим знак » 0,\] так как \(\sqrt <3>1,\) то \(\log_4<\sqrt<3>> 1,\) то \(\log_4 <3,5>3^1\; и\; 3>1,\) то \(\log_3 <3,5>> 1.\)
3) пусть \(x = 9; \;x \in (4;+\infty)\) \[\log_3
По рисунку формулируем ответ.
Сравните все три способа решения для этого вовсе не сложного неравенства и определитесь, какой вариант наиболее приемлем для вас.
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Решение логарифмических уравнений — примеры с решениями
Решение простейших логарифмических уравнений
Как известно, решение простейшего логарифмического уравнения logax=b — это x=a b . Другими словами, простейшее логарифмическое уравнение logax=b имеет единственный корень, которым является степень a b .
Первый пример. Проще некуда.
Решите уравнение log5x=2
Все понятно без слов:
log5x=2
x=5 2
x=25
При решении простейших логарифмических уравнений переход от logax=b к x=a b , обычно, не представляет сложности. Часто, куда сложнее вычислить значение степени a b или упростить ее вид. Следующие примеры иллюстрируют сказанное.
Второй пример. А вычислить значение?
Решите логарифмическое уравнение
Это простейшее логарифмическое уравнение. Оно имеет единственный корень . Очевидно, полученная степень нуждается в доработке.
Сначала заменим квадратный корень из семи степенью: .
Остается вспомнить, как определяется степень с отрицательным показателем, и закончить вычисления:
На этом решение простейшего логарифмического уравнения завершено.
Третий пример. Извольте упростить.
Начинаем со стандартного при решении простейших логарифмических уравнений перехода:
Надо бы упростить полученную степень.
Возвести дробь в минус первую степень – это кувыркнуть ее вверх ногами:
Теперь глаза мозолит иррациональность в знаменателе, исправим эту ситуацию:
Таким образом, — искомое решение простейшего логарифмического уравнения.
Решение логарифмических уравнений разными методами
Сейчас пройдемся по всем основным методам решения логарифмических уравнений, и рассмотрим решения наиболее характерных и интересных, по нашему мнению, логарифмических уравнений.
по определению логарифма
По определению логарифма в первую очередь проводится решение логарифмических уравнений logaf(x)=b , где a и b — числа, причем a>0 , a≠1 , а f(x) – выражение с переменной x , таких как log2(x 2 +4·x+3)=3 , и др. Решение состоит в переходе от уравнения logaf(x)=b к уравнению f(x)=a b . Например, решение логарифмического уравнения log2(x 2 +4·x+3)=3 с опорой на определение логарифма заменяется решением уравнения x 2 +4·x+3=2 3 .
На определение логарифма можно опираться и при решении логарифмических уравнений logh(x)f(x)=g(x) , таких как logx(x 2 −3·x+6)=2 , log2(9−2 x )=3−x , logx(3·x lgx +4)=2·lgx и др. Решение уравнения logh(x)f(x)=g(x) заключается в решении уравнения f(x)=(h(x)) g(x) на области допустимых значений (ОДЗ) для исходного уравнения. Например, чтобы решать логарифмическое уравнение logx(x 2 −3·x+6)=2 по определению логарифма, надо решить уравнение x 2 −3·x+6=x 2 , и взять все корни, принадлежащие ОДЗ для исходного уравнения.
- Чтобы решить логарифмическое уравнение logaf(x)=b по определению логарифма, надо перейти к уравнению f(x)=a b и найти его решение.
- А чтобы решить по определению логарифма уравнение logh(x)f(x)=g(x) , надо перейти к уравнению f(x)=(h(x)) g(x) , решить его, и взять корни, принадлежащие ОДЗ для исходного логарифмического уравнения.
Рассмотрим примеры решения логарифмических уравнений.
Обычно решение оформляется кратко:
А теперь поясним, какие рассуждения за всем этим скрываются.
Заданное логарифмическое уравнение имеет вид logaf(x)=b , где f(x)=2·x−4 , a=1/2 , b=−2 . Такое логарифмическое уравнение можно решать по определению логарифма, то есть, заменять решение уравнения logaf(x)=b решением уравнения f(x)=a b .
Итак, переходим от исходного уравнения к уравнению . Это рациональное уравнение, решаем его:
Так получено решение исходного логарифмического уравнения.
Пример. Не забыть про проверку.
Решите логарифмическое уравнение logx(−x 2 +5·x+3)=2
Заданное уравнение можно рассматривать как уравнение logh(x)f(x)=g(x) , где f(x)=−x 2 +5·x+3 , h(x)=x , g(x)=2 , и мы знаем, что такие уравнения можно решать по определению логарифма. Решение этим методом на первом этапе предполагает переход от уравнения logh(x)f(x)=g(x) к уравнению f(x)=(h(x)) g(x) . Имеем −x 2 +5·x+3=x 2 .
Теперь нам надо решить полученное уравнение −x 2 +5·x+3=x 2 . Оно сводится к квадратному уравнению 2·x 2 −5·x−3=0 . Решаем его:
Остается пройти последний шаг решения логарифмического уравнения по определению логарифма – выяснить, какие из корней принадлежат ОДЗ для исходного уравнения. ОДЗ для исходного логарифмического уравнения logx(−x 2 +5·x+3)=2 определяется системой .
Очевидно, не удовлетворяет второму условию, значит, это посторонний корень для исходного уравнения. А корень x2=3 удовлетворяет всем условиям: . Значит, x2=3 – это корень уравнения logx(−x 2 +5·x+3)=2 .
На этом решение завершено. Уравнение имеет единственный корень 3 .
Естественно, так подробно решение не описывают. Обычно его оформляют кратко, но без ущерба для логики действий, например, так:
методом потенцирования
Метод потенцирования применяется для решения логарифмических уравнений, части которых являются логарифмами с одинаковыми основаниями, например, log5(x−1)=log57 , и др. Решение логарифмических уравнений методом потенцирования состоит в переходе от уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения. Так решение уравнения можно заменить решением уравнения x+1=x 2 −1 на ОДЗ для исходного уравнения.
Название метода становится понятным, если вспомнить, что потенцирование – это восстановление выражения по его логарифму.
Обосновать метод можно, сославшись на свойства логарифмов. Из них мы знаем, что логарифмы двух положительных чисел с одинаковыми положительными и отличными от единицы основаниями равны тогда и только тогда, когда равны сами числа, то есть, , a>0 , a≠1 , b1>0 , b2>0 . Так вот переход от логарифмического уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) — это аналог замены logab1=logab2 на b1=b2 , а нахождение в рамках ОДЗ для исходного уравнения – это аналог выполнения условий a>0 , a≠1 , b1>0 , b2>0 .
Итак, чтобы решить логарифмическое уравнение logh(x)f(x)=logh(x)g(x) методом потенцирования, надо
- Перейти к уравнению f(x)=g(x) .
- Решить полученное уравнение.
- И взять корни, принадлежащие ОДЗ для исходного уравнения, остальные отбросить как посторонние. Другими словами, провести отсеивание посторонних корней.
Остается рассмотреть пример с решением.
Мы видим, что части уравнения являются логарифмами с одинаковыми основаниями. Подобные логарифмические уравнения удобно решать методом потенцирования.
Согласно выбранному методу, переходим от исходного уравнения к уравнению x+1=x 2 −1 .
Теперь нам надо решить полученное уравнение x+1=x 2 −1 . Перенос слагаемых из одной части уравнения в другую с противоположным знаком и приведение подобных слагаемых дает квадратное уравнение x 2 −x−2=0 , которое можно решить, например, через дискриминант:
Остается проверить принадлежность найденных корней области допустимых значений переменной x для исходного уравнения. Для нашего логарифмического уравнения ОДЗ определяют два условия x+1>0 и x 2 −1>0 . Очевидно, x1=−1 не удовлетворяет первому условию ( −1+1>0 — неверное), значит, это посторонний корень для решаемого уравнения. А корень x2=2 удовлетворяет обоим условиям ( 2+1>0 – верное, 2 2 −1>0 — верное). Значит, он является корнем уравнения .
На этом решение логарифмического уравнения методом потенцирования завершено. Уравнение имеет единственный корень, им является число 2 .
методом разложения на множители
Пример. Все как всегда.
Решение логарифмического уравнения можно провести методом разложения на множители, так как в левой части уравнения находится произведение двух выражений с переменной, а в правой – нуль.
Первый шаг – переход к совокупности уравнений:
Второй шаг – решение полученных логарифмических уравнений.
Первое уравнение можно решить по определению логарифма, а второе — методом потенцирования, после предварительного переноса второго логарифма в правую часть со знаком «плюс»:
На последнем шаге остается выяснить, принадлежат ли найденные корни 2 и 5 ОДЗ для решаемого логарифмического уравнения :
На этом решение логарифмического уравнения методом разложения на множители завершено.
путем введения новой переменной (замены переменной)
Решение логарифмических уравнений методом введения новой переменной, как правило, проводится в следующих типичных ситуациях:
- Когда переменная находится в составе некоторой сложной функции, как, например, в уравнении
- Когда переменная фигурирует в нескольких одинаковых выражениях и нигде более. Вот примеры логарифмических уравнений, соответствующие сказанному:
(часто, одинаковые выражение с переменной прячут за свойствами степеней, и приведенное выше в пример логарифмическое уравнение, скорее, будет выглядеть так или так )
Пример №1. Вводить или не вводить?
Решите логарифмическое уравнение
Введение новой переменной 2−log2x=t позволяет перейти от логарифмического уравнения к сравнительно простому уравнению t 4 =16 с понятной структурой и очевидным решением:
Возврат к старой переменной дает два логарифмических уравнения 2−log2x=2 и 2−log2x=−2 , решив которые находим интересующее нас решение исходного уравнения:
Итак, логарифмическое уравнение имеет два корня 1 и 16 .
В заключение заметим: введение новой переменной в подобных и, прямо скажем, простых ситуациях настолько прозрачно, что его проводят «в уме», и не отражают в решении:
Пример №2. Оказывается, оно квадратное.
Выражения 2 2·(log5x) 2 и 2 (log5x) 2 , в которых содержится переменная в заданном логарифмическом уравнении, почти одинаковые. Различие вносит лишь число 2 в показателе первой степени. Здесь несложно догадаться, что по свойству степени в степени, выражение 2 2·(log5x) 2 можно переписать как (2 (log5x) 2 ) 2 , что открывает дорогу к замене переменной 2 (log5x) 2 =t и переходу к квадратному уравнению t 2 −15·t−16=0 с новой переменной t .
Итак, проведем решение логарифмического уравнения через замену переменной:
Пример. Взаимно обратные логарифмы.
Решите логарифмическое уравнение
Здесь полезно вспомнить следствие из формулы перехода к новому основанию логарифма, которому отвечает формула logab=1/logba , a>0 , a≠1 , b>0 , b≠1 . Так возникает идея обозначить один из логарифмов в заданном логарифмическом уравнении за t , тогда другой логарифм будет выражаться через новую переменную t как 1/t .
Остается вернуться к старой переменной x , и закончить решение. Мы принимали logx+3(3·x+13)=t и нашли t=2 , поэтому
Итак, логарифмическое уравнение имеет единственное решение 1 .
дробь равна нулю
Решите логарифмическое уравнение
Решение логарифмических уравнений, в левых частях которых находится дроби, а в правых – нули, проводится в соответствии с методом решения уравнений «дробь равна нулю». При этом надо приравнять числитель дроби к нулю, и решить это уравнение на ОДЗ для исходного уравнения.
Итак, решение начинаем с приравнивания к нулю числителя дроби из левой части заданного уравнения. Это дает уравнение log3(x−3) 2 −4=0 , которое равносильно уравнению log3(x−3) 2 =4 . Решение полученного логарифмического уравнения можно провести по определению логарифма:
Остается проверить, принадлежат ли найденные корни области допустимых значений переменной x для исходного логарифмического уравнения. В нашем случае условий, которые определяют ОДЗ, довольно много, поэтому, кажется, рациональнее действовать через непосредственную подстановку. Подставим найденные корни в исходное уравнение и посмотрим, что при этом получается.
Подстановка x1=12 дает верное числовое равенство
Поэтому, 12 является корнем.
При подстановке x2=−6 получается не имеющее смысла выражение , так как под знаками логарифмов в знаменателе – отрицательные числа. Значит, −6 – посторонний корень.
методом логарифмирования
Решение логарифмических уравнений в определенных случаях приходится проводить через логарифмирование обеих частей уравнения. Обычно, к логарифмированию прибегают тогда, когда в одной части уравнения находится показательно степенное выражение, а в другой – положительное число, как в следующих уравнениях , и т.п.
Давайте решим одно из них, чтобы стало понятно, что дает логарифмирование уравнения.
Пример. Дожили, лог уравнения логарифмируем
Данное уравнение – это типичный представитель уравнений, для решения которых используется метод логарифмирования. В левой части уравнения – степень, на ОДЗ для уравнения эта степень принимает только положительные значения. Это открывает возможность прологарифмировать обе части заданного уравнения. В нашем случае логарифмирование целесообразно проводить по основанию 2 , так как в исходном уравнении присутствует логарифм с таким основанием. Так и поступим:
Для нашего уравнения ОДЗ определяется условием x>0 . Поэтому, мы спокойно можем вынести степень из-под знака логарифма, оперевшись на соответствующее свойство логарифмов (подробнее про решение логарифмических уравнений через преобразования поговорим в одном из следующих пунктов):
И это, собственно, то, ради чего логарифмирование затевалось – привести логарифмическое уравнение к более простому и привычному виду. Дальнейшие преобразования не требуют комментирования:
Полученное логарифмическое уравнение, очевидно, можно решить методом замены переменной:
графическим методом
К решению логарифмических уравнений графическим методом обычно прибегают тогда, когда, во-первых, функции, отвечающие частям заданного логарифмического уравнения, довольно простые в плане построения их графиков, и, во-вторых, не видно других более простых вариантов получить решение.
Пример. Графически так графически.
Сколько корней имеет уравнение
Сама формулировка задания подсказывает, что, скорее всего, решить уравнение, что называется, в лоб, и указать не только количеств корней, но и сами эти корни, не выйдет. Иначе бы вопрос стоял «решить уравнение». Действительно, путей решения этого уравнения не видно.
Однако, количество корней удобно определять по графикам функций, соответствующих частям уравнения. Более того, в данном случае построить графики этих функций довольно просто. Нам хорошо известны функции и y=log2x и их графики. Графики интересующих нас функций и y=log2(x−2) будут иметь схожую геометрию с точностью до преобразований растяжения и симметрии. Поэтому, нам достаточно взять несколько опорных точек, чтобы изобразить нужные кривые. Давайте получим их, учитывая, что область определения функции — это x≤15/4 , а область определения функции y=log2(x−2) — это x>2 .
Отмечаем эти точки на плоскости в прямоугольной системе координат, соединяем их плавными линиями, и чертеж готов:
Видно, что графики имеют одну точку пересечения на отрезке от трех до пятнадцати четвертых. Больше их быть не может, так как функция убывает на указанном отрезке от до нуля, а функция y=log2(x−2) возрастает на этом отрезке от нуля до log2(7/4) .
Это позволяет нам утверждать, что уравнение имеет один корень.
через подбор корня и возрастание-убывание функций
Решение логарифмических уравнений иногда приходится проводить, основываясь на возрастании и убывании функций, соответствующих частям уравнения. Это касается ситуаций, когда простые и привычные пути решения не просматриваются, но зато очевиден или легко подбирается корень логарифмического уравнения, а также легко обосновывается возрастание и убывание соответствующих функций. Приведем пример.
Пример. Подбор и единственность.
Для заданного уравнения не видно других подходов к решению, кроме как обращаться к функциям и их свойствам. Можно строить графики, но делать это для функции, отвечающей правой части уравнения, не очень приятно из-за довольно «большого» числа 11 и довольно «высокой» степени 5 . Попробуем обойтись без чертежа.
Вместо этого обопремся на возрастание логарифмической функции, отвечающей левой части уравнения, и убывание функции, отвечающей правой части уравнения (она убывает, как возрастающая от убывающей). Это позволяет утверждать, что если уравнение имеет корень, то он единственный. А найти корень позволяет подбор по рекомендациям, данным в статье, посвященной методу решения уравнений через возрастание-убывание, – им является число 10 .
На этом решение логарифмического уравнения завершено.
методом оценки
Пример. Оценить и дорешать.
Своего рода оценочная классика: логарифм, синус, косинус, корень – все в одном уравнении. Итак, пробуем провести решение уравнения методом оценки. Но сначала, все же, квадратный корень из квадрата заменим модулем:
Теперь к оценкам.
Косинус принимает значения из отрезка −1 до 1 , а его модуль – [0, 1] . Следовательно, . С другой стороны, как четная степень, откуда . Таким образом, значения выражения из левой части уравнения не превосходят 1 , а значения выражения из правой части уравнения не меньше 1 . Это позволяет нам заменить решение исходного уравнения решением следующей системы
Что делать с первым уравнением системы — сразу не понятно, зато вполне реально получить решение второго логарифмического уравнения:
Теперь путем подстановки выясним, удовлетворяют ли найденные корни логарифмического уравнения 2 и 3 первому уравнению системы, а значит, системе в целом, и исходному уравнению.
Давайте начнем с числа 3 , с ним все просто:
Это верное равенство, следовательно, 3 – решение системы и корень исходного уравнения.
А вот с числом 2 придется повозиться.
Это равенство неверное (обоснуем чуть ниже), следовательно, 2 – не является решением системы, и не является корнем исходного уравнения.
Таким образом, уравнение имеет один единственный корень 3 .
А вот обещанное обоснование.
Модуль косинуса равен единице, если аргумент косинуса равен . А не равно sin10 ни при каком целом k . Действительно, при k=0 , очевидно, sin10≠0 . При любом другом целом k равенство неверное, так как значения синуса находятся в отрезке от −1 до 1 .
через ОДЗ
Решение логарифмических уравнений часто требует нахождения ОДЗ: когда для проведения преобразований, когда для проверки. А порою ОДЗ позволяет даже получить решение.
Пример. ОДЗ от безысходности.
Беглый анализ уравнения, можно сказать, ставит в тупик относительно способа его решения. И почти единственным и, так или иначе, адекватным мероприятием выглядит нахождение ОДЗ. Что называется, в любом случае пригодится.
Вот как все обернулось: ОДЗ есть пустое множество. Следовательно, уравнение не имеет корней.
методом освобождения от внешней функции
Признаемся, почти никогда для решения логарифмических уравнений не приходилось прибегать к методу освобождения от внешней функции. Однако для полноты картины не помешает привести решение соответствующего примера.
Пример. Попробуй разгляди.
Найдите решение уравнения
Как тут действовать? Непонятно, что здесь можно предложить в альтернативу методу освобождения от внешней функции.
А так заданное логарифмическое уравнение можно рассматривать как уравнение , где функция f такая, что . Очевидно, f – возрастающая функция как сумма двух возрастающих. Это позволяет освободиться от внешней функции f в уравнении , то есть, на ОДЗ перейти к уравнению .
Здесь заметим, что область допустимых значений переменной для полученного уравнения совпадает с ОДЗ для исходного уравнения (она такова ). Значит, решение полученного уравнения является решением исходного уравнения.
Остается решить логарифмическое уравнение , что можно сделать через потенцирование:
Решение логарифмических уравнений через преобразование
Редкий раз решение логарифмических уравнений обходится без проведения преобразований. Характерными для логарифмических уравнений являются преобразования, проводящиеся на базе свойств корней и степеней. Все они по отдельности разобраны в статье «Преобразование логарифмических уравнений». Здесь мы рассмотрим примеры решения логарифмических уравнений со сравнительно сложными последовательностями преобразований.
Для начала напомним о необходимости использования модулей при вынесении четных показателей степеней из-под знаков логарифмов, а также при переходе от логарифмов произведений (частных) к суммам (разностям) логарифмов.
Пример. Про модуль не забыть.
Решите логарифмическое уравнение
Просматривается возможность прийти к одинаковым логарифмам в левой части уравнения. Для начала вынесем показатель 2 из-под знака логарифма, и так как он есть четное число, то не забудем про модуль:
Для раскрытия модуля нам потребуется ОДЗ для исходного уравнения:
С учетом этого, имеем
Дальше все просто:
Теперь еще раз обратим внимание на преобразование квадратов, кубов и других степеней логарифмов. Уж очень часто приходится видеть неверные преобразования, типа , вместо , или , вместо и т.п.
Пример. Квадраты логарифмов.
Просматривается возможность упростить вид заданного логарифмического уравнения. Для начала перепишем его как , чтобы не наделать ошибок при преобразовании квадратов логарифмов. Дальше все довольно прозрачно:
Теперь пора ввести новую переменную:
Остается вернуться к старой переменной:
Наконец, рассмотрим пример решения довольно сложного логарифмического уравнения, где сильно переплетены степени и логарифмы.
Просматриваются черты основного логарифмического тождества. Сейчас поработаем в этом направлении. Но сначала давайте найдем область допустимых значений переменной x – она бывает нужна при проведении преобразований и при проведении проверки. Тем более, в нашем случае ОДЗ находится легко:
Теперь приступаем к преобразованию:
А дальше все легко:
При найденных значениях переменной знаменатели дробей в уравнении в нуль не обращаются, а также 0 и 2 принадлежат ОДЗ для исходного уравнения, следовательно, являются его корнями.
Решение однородных логарифмических уравнений
В задачниках встречаются логарифмические уравнения, которые являются однородными уравнениями относительно некоторых логарифмов. Например, lg 2 (x+1)−lg(x+1)·lg(x−1)−2·lg 2 (x−1)=0 – это логарифмическое уравнение, однородное относительно логарифмов lg(x+1) и lg(x−1) .
Решение однородных логарифмических уравнений завязано на преобразовании, заключающемся в делении обеих частей уравнения на «старшую» степень одного из логарифмов, что в дальнейшем позволяет ввести новую переменную. При этом необходимо отдельно проверять, не являются ли корнями уравнения те значения переменной, при которых обращается в нуль логарифм, на который планируется проводить деление. Давайте обратимся к конкретному примеру.
Возьмем наше уравнение lg 2 (x+1)−lg(x+1)·lg(x−1)−2·lg 2 (x−1)=0 . Оно, как мы отметили, является однородным относительно логарифмов lg(x+1) и lg(x−1) . Давайте разделим обе части этого уравнения на старшую степень второго из этих логарифмов, то есть, на lg 2 (x−1) . Но, как известно, делить обе части уравнения мы имеем право только на выражение, не обращающееся в нуль, в противном случае можно потерять корни. Поэтому, стоит отдельно проверить, не являются ли корнями уравнения значения переменной, при которых lg 2 (x−1)=0 , а уже после этого спокойно проводить задуманное деление, не опасаясь потерять корни. В нашем случае lg 2 (x−1)=0 только при x=2 . Но x=2 не является решением исходного уравнения, так как его подстановка в исходное уравнение дает неверное числовое равенство. Теперь можно переходить к делению, считая lg 2 (x−1)≠0 . Имеем:
Дальше напрашиваются следующие преобразования
Остается закончить решение, воспользовавшись методом введения новой переменной. Приняв , имеем
Решение логарифмического уравнения методом разложения на множители.
Данный метод применяется в том случае, когда левую часть уравнения можно разложить на множители, а в правой части получить 0.
В этом случае следует пользоваться правилом:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей, входящих в данное произведение равен нулю, а остальные при этом имеют смысл.
2.Рассмотрим метод разложения на множители на конкретном примере.
Задание. Решите уравнение:
О.Д.З.:
Перенесем все слагаемые из правой части уравнения в левую:
В левой части уравнения сгруппируем слагаемые 1 с 3 и 2 с 4:
Выносим за скобку общую скобку:
Применим правило произведения:
Ответ:
3.Решите уравнение: 
Перенесем все слагаемые из правой части уравнения в левую:
В левой части уравнения сгруппируем слагаемые 1 со 2 и 3 с 4:
Выносим за скобку общую скобку: _______________________
Применим правило произведения:
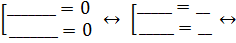

Проверка на вхождение в О.Д.З.?
Ответ: 
Выберите представителей от группы, которые познакомят остальных учащихся с изученным методом, изложат ход решенного вами уравнения.
Дескриптор: — знает метод введения новой переменной при решении
— определяет по типу уравнения метод решения;
— применяет свойства логарифма;
— решает уравнение данным методом.
1.Решите уравнение:
1) 10; 2) 8; 3) 4; 4) 11
2. Решите уравнение:
1) 2; 2) -7; 3) 11; 4) 1
3. Решите уравнение:
1) 2; 2) 3; 3) 0; 4) 1
4. Решите уравнение:
1) 4; 2) 2; 3) 7; 4) 5
5. Укажите промежуток, содержащий корень уравнения
1)  ; ; | 2) 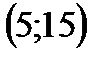 ; ; | 3) 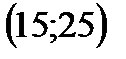 ; ; | 4) 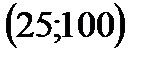 . . |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| ответ |
1.Решите уравнение:
1) 7; 2) 3; 3) 11; 4) 4
2. Решите уравнение:
1) 4; 2) 0,5; 3) 1; 4) 2
3. Решите уравнение:
1) 4; 2) 1; 3) 0,8; 4) -1
4. Решите уравнение:
1) 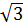
5. Укажите промежуток, содержащий корень уравнения
1)  ; ; | 2)  ; ; | 3) 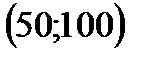 ; ; | 4)  . . |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| ответ |
1.Решите уравнение:
1) 1; 2) -1; 3) 19; 4) 0
2. Решите уравнение:
1) -6; 2) 1; 3) 0,75; 4) 1,8
3. Решите уравнение:
1) 0,4; 2) 17; 3) 2; 4) 8
4. Решите уравнение:
1)1; 2) 8; 3) 16; 4) 2
5. Укажите промежуток, содержащий корень уравнения
1)  ; ; | 2)  ; ; | 3) 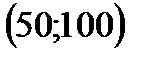 ; ; | 4)  . . |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| ответ |
1.Решите уравнение:
1) 5; 2) 4; 3) 17; 4) 13
2. Решите уравнение:
1) 1; 2) -2; 3) 3; 4) 2
3. Решите уравнение:
1) 0,3; 2) 1; 3) 4; 4) 2
4. Решите уравнение:
5. Укажите промежуток, содержащий корень уравнения
1)  ; ; | 2) 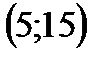 ; ; | 3) 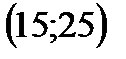 ; ; | 4) 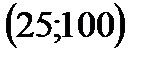 . . |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| ответ |
1.Решите уравнение:
1) 1; 2) 7; 3) 25; 4) 27
2. Решите уравнение:
1) 5; 2) 6; 3) 7; 4) 8
3. Решите уравнение:
1) 0,3; 2) 1; 3) 4; 4) 2
4. Решите уравнение:
1)3; 2) 2; 3) 1; 4) 0,5
5. Укажите промежуток, содержащий корень уравнения
1)  ; ; | 2) 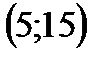 ; ; | 3) 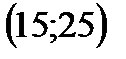 ; ; | 4) 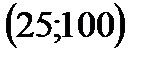 . . |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| ответ |
| вариант | 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 3 | 4 | 3 | 4 |
| 2 | 1 | 4 | 2 | 2 | 4 |
| 3 | 2 | 2 | 3 | 1 | 4 |
| 4 | 3 | 4 | 4 | 1 | 4 |
| 5 | 3 | 2 | 4 | 4 | 4 |
Критерии оценивания: 5 баллов – 5 правильно решенных задач;
http://www.cleverstudents.ru/equations/solving_logarithmic_equations.html
http://lektsia.com/15×9970.html