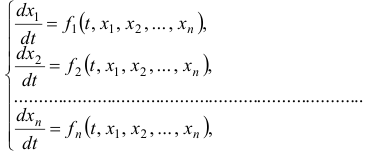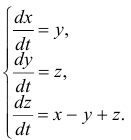Решение методом сведение к одному уравнению

Сведение системы к одному дифференциальному уравнению высшего порядка

Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входит независимая переменная, искомые функции и их производные.

Решение системы, состоящей из нескольких уравнений с таким же числом неизвестных функций, можно привести к решению дифференциального уравнения с одной неизвестной функцией.

Нормальная система уравнений:

как правило, может быть заменена одним дифференциальным уравнением, порядок которого равен порядку системы.

Пример:

Найти общее решение системы уравнений

Решение:

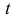
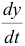
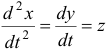
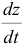
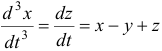
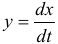
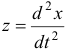
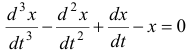
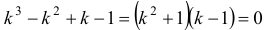
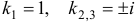
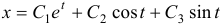
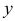
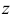
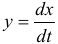
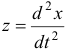
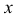
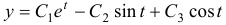
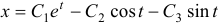
Продифференцировав первое уравнение по , заменим производную ее выражением из второго уравнения: . Продифференцировав полученное уравнение еще раз, заменим производную ее выражением из третьего уравнения: . Подставляя в последнее уравнение и , окончательно получим . Решим это уравнение. Соответствующее ему характеристическое уравнение имеет корни . Следовательно, . Функции и в соответствии с соотношениями и после дифференцирования полученного для выражения имеют вид: и .

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Метод исключения — сведение системы ДУ к одному уравнению

Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

это уравнение заменяется нормальной системой уравнений

Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка

эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения .

Проиллюстрируем этот метод на примере системы двух уравнений:

Здесь — постоянные коэффициенты, а и — заданные функции; и — искомые функции. Из первого уравнения системы (1) находим

Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение второго порядка относительно

где — постоянные. Отсюда находим . Подставив найденное выражение для и в (2), найдем .

Пример 1. Проинтегрировать систему уравнений

Решение. Из первого уравнения системы (3) находим , тогда

Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка

Общее решение уравнения (5)

Находя производную по от (6), получаем

Общее решение системы (3):

Пример 2. Решить задачу Коши для системы

Решение. Из второго уравнения системы (7) находим

Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение , общее решение которого

Подставляя (11) в (9), найдем . Общее решение системы (7)

При начальных условиях (8) из (12) получим систему уравнений для определения

решая которую, найдем . Подставляя эти значения и в (12), получаем решение поставленной задачи Коши:

Пример 3. Решить систему уравнений

Решение. Из первого уравнения системы находим

Подставляя эти выражения для и во второе уравнение, получаем

Считая , из последнего уравнения имеем и после интегрирования получим . Теперь легко находим

Общее решение данной системы

Замечание. Не всякая система дифференциальных уравнений может быть сведена к одному уравнению более высокого порядка. Например,

не сводится к одному уравнению второго порядка. Ее общее решение .

Методы решения уравнений. Сведение к однородному.. — презентация

Презентация была опубликована 8 лет назад пользователемwiki.vspu.ru

Похожие презентации

Презентация на тему: » Методы решения уравнений. Сведение к однородному..» — Транскрипт:

1 Методы решения уравнений. Сведение к однородному.

2 Над проектом работал Шантыр Антон.

3 Применение метода сведения к однородному в решении уравнений. Воспользовавшись тригонометрическим тождеством уравнение вида R(sinx+cosx,sinxcosx)=0, где, R-рациональная функция может быть сведено к уравнению относительно неизвестного t=sinx+cosx. Из которого следует,что sinxcosx= Учитывая это, уравнение можно привести к виду Аналогично можно преобразовать уравнение вида Заменой sinx-cosx=t сводится к уравнению

4 Решение задач на этот метод. Номер 501 (а). Решая эти, уравнения у меня возникли трудности. Эти уравнение можно решить только моим методом. Sin2x+2sinx=2-2cosx; 2sinx+2cosx+sin2x-2=0; Пусть sinx+cosx=t; sinxcosx= Sin2x=2sinxcosx; Значит, 2t+ -1-2=0; +2t-3=0; D=4+12=16; =-3; =1; -3 условию задачи не корректно. Значит, sinx+cosx=1; Возведем обе части уравнения в квадрат: 1+sin2x=1; Sin2x=0; 2x=пк; X= Ответ:

5 Другие методы решения тригонометрических уравнений. 1. Решение уравнений разложением на множители. Решить уравнение: sin4x=3cos2x; Решение: воспользуемся фор- мулой двойного угла и запишем уравнение в виде: 2sin2xcos2x=3cos2x; Перенесем все члены уравнения влево и разложим левую часть на множители: 2sin2xcos2x-3cos2x=0; (2sin2x-3) cos2x=0; Решим два уравнения по отдельрости: 2sin2x-3=0; 2sin2x=3; sin2x=1,5; нет решений. Cos2x=0; 2x= X= Ответ:

6 Преобразование суммы или разности в произведение. Решить уравнение: cos3x+sin2x-sin4x=0; Решение: Преобразуем разность синусов в произведение:cos3x+(-2sinxcos3x)=0; Cos3x(1-2sinx)=0; Полученное уравнение яв- ляется совокупностью двух уравнений: cos3x=0; sinx=0,5; Cos3x=0; 3x= x= sinx=0,5; x= Объединив корни получим ответ: Ответ:

7 Преобразование произведения в сумму. Решить уравнение: sin5xcos3x=sin6xcos2x; Решение:Применим к обеим частям уравне- ния формулу преобразования произведения в сумму. Получим: 0,5(sin8x+sin2x)=0,5(sin8x+ sin4x), которое можно привести к виду: sin2x- sin4x=0; Преобразуем разность в произведе- ние: -2sinxcos3x=0; sinx=0; x=пк; Cos3x=0; 3x= x= Ответ: x=пк; x=.

8 Сведение к рациональным уравнениям. Решить уравнение: 3sinx- =0; Решение: Применим основное тригонометри- ческое тождество: 3sinx-2( =0; Это уравнение перепишем как квадратное от- носительно sinx: Сделаем замену t=sinx и придем к квадратно- му уравнению: Корни этого уравнения -2 и 0,5. -2 не корректно условию. Значит, sinx=0,5. X= Ответ:

9 Однородные тригорометрические уравнения. Однородными уравнениями первой степени относи- тельно sinx называются уравнения вида asinx+bcosx =0; где a и b – некоторые числа. Решить уравнение: sinx-cos=0; Решение. Решением этого уравнения де- ление обеих частей уравнения на sinx или на cosx. Разделим обе части на cosx. Это может привести к потере одного из значений x. Но значение cosx=0; не дает решения данного уравнения. Значит, с легкос – тью можно делить на cosx. Выполнив деление,полу – чим tgx=1. x= Ответ:

10 Решение задач на мой метод. Номер 501(б). Решить: 4sin2x+8sinx-8cosx-7=0; Пусть sinx-cosx=t; sinxcosx= ; sin2x=2sincosx; 4sin2x=8sinxcosx; Получим, D=64-48=16; t=0,5; t=1,5; T=1,5 не корректно условию. Значит, t=0,5. sinx-cosx=0,5; Возведем обе части в квадрат, 1-sin2x=0,25; sin2x=0,75; 2X= x= Ответ: