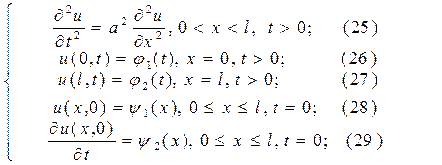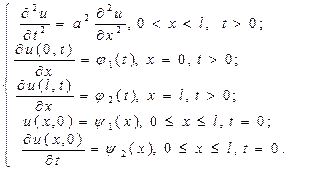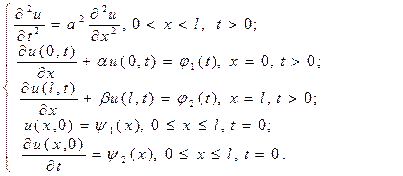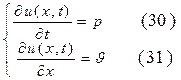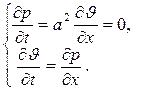Решение начально краевой задачи для гиперболического уравнения

НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ С ЭЛЛИПТИЧЕСКИМ ОПЕРАТОРОМ ПРОИЗВОЛЬНОГО ПОРЯДКА Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Ашуров Р.Р., Мухиддинова А.Т.

В настоящей работе исследуется начально-краевые задачи для гиперболических уравнений , эллиптическая часть которых имеет наиболее общий вид и определена в произвольной многомерной области (с достаточно гладкой границей). Установливаются требования на правую часть уравнения и начальные функции, при которых к рассматрываемую задачу применим классический метод Фурье . Другими словами, доказывается методом Фурье существование и единственность решения смешанной задачи и показана устойчивость найденного решения от данных задачи: от начальных функций и правой части уравнения. Введено понятие обобщенного решения и доказана теорема о его существования . Аналогичные результаты справедливы и для параболических уравнений.

Похожие темы научных работ по математике , автор научной работы — Ашуров Р.Р., Мухиддинова А.Т.

INITIAL-BOUNDARY VALUE PROBLEM FOR HYPERBOLIC EQUATIONS WITH AN ARBITRARY ORDER ELLIPTIC OPERATOR

An initial-boundary value problem for a hyperbolic equation with the most general elliptic differential operator, defined on an arbitrary bounded domain, is considered. Uniqueness , existence and stability of the classical solution of the posed problem are proved by the classical Fourier method . Sufficient conditions for the initial function and for the right-hand side of the equation are indicated, under which the corresponding Fourier series converge absolutely and uniformly. The notion of a generalized solution is introduced and existence theorem is proved. Similar results are formulated for parabolic equations too.

Текст научной работы на тему «НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ С ЭЛЛИПТИЧЕСКИМ ОПЕРАТОРОМ ПРОИЗВОЛЬНОГО ПОРЯДКА»

Вестник КРАУНЦ. Физ.-мат. науки. 2020. Т. 30. № 1. C. 8-19. ISSN 2079-6641

DOI: 10.26117/2079-6641-2020-30-1-8-19 МАТЕМАТИКА

НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ С ЭЛЛИПТИЧЕСКИМ ОПЕРАТОРОМ ПРОИЗВОЛЬНОГО ПОРЯДКА

Р. Р. Ашуров, А.Т. Мухиддинова

Институт Математики имени В. И. Романовского Академии наук Узбекистана, г. Ташкент, ул. Мирзо Улугбека 85, 100170, Узбекистан E-mail: ashurovr@gmail.com,oqila1992@mail.ru

В настоящей работе исследуется начально-краевые задачи для гиперболических уравнений, эллиптическая часть которых имеет наиболее общий вид и определена в произвольной многомерной области (с достаточно гладкой границей). Установливаются требования на правую часть уравнения и начальные функции, при которых к рассматрываемую задачу применим классический метод Фурье. Другими словами, доказывается методом Фурье существование и единственность решения смешанной задачи и показана устойчивость найденного решения от данных задачи: от начальных функций и правой части уравнения. Введено понятие обобщенного решения и доказана теорема о его существования. Аналогичные результаты справедливы и для параболических уравнений.

Ключевые слова: гиперболическое уравнение, начально-краевые задачи, метод Фурье, существование, единственность и устойчивость классического решения, обобщенное решение

© Ашуров Р. Р., Мухиддинова А.Т., 2020

Известно (см., например [1], стр. 144, [2], стр. 278-280, [3]- [6]) что большое число задач о колебаниях стержней, пластин и т.д. приводит к дифференциальным уравнениям высокого порядка. В качестве примера уравнения 4-го порядка можно взять задачу о колебаниях тонкого прямоугольного стержня; определение формы колебаний стержня и его частоты сводится к решению «уравнения поперечных колебаний стержня»: и« + а2ихххх = 0. В работах К.Б. Сабитова [3]- [5] детально изучены различные начально-краевые задачи для этого уравнения. Основным аппаратом исследования в этой работе является классический метод Фурье, основанный на

свойствах тригонометрияеских функций. Результаты этих исследований легко обобщаются на случае уравнения

ип + а (и хххх + иуууу + игггг) — ° г > ° (x, y, е

когда область О является произведением трех одномерных интервалов [6], так как собственные функции соответствующих спектральных задач являются произведением тригонометрических функций. Естественно, исходя из физического смысла задачи, представляет интерес рассмотрение аналогичных задач для произвольных ограниченных пространственных областей О.

В настоящей работе исследуется начально-краевые задачи для гиперболических уравнений, эллиптическая часть которых определена в произвольной М-мерной области О (с достаточно гладкой границей дО) и имеет наиболее общий вид.

Пусть А(х,О) — £ аа(х)Оа — произвольный положительный формально самосо-

и(х,0) — ф(х), иг(х,0) — у(х), х е О; (2)

Буи(х,г)— £ Ьа,у(х)Оаи(х,г) — 0, 0 ) все производные, которые входят в уравнение (1), и удовлетворяющую всем условиям смешанной задачи (1)-(3) в обычном классическом смысле.

Обратим внимание на то, что требование непрерывности в замкнутом цилиндре всех производных, входящих в уравнение (1), определяемого решения не вызвано существом дела. Однако, с одной стороны, единственность именно такого решения доказывается достаточно просто, а с другой стороны, решение, найденное методом Фурье, удовлетворяет указанным выше условиям.

Классическое решение мы иногда будем называть просто решением смешанной задачи (1)-(3).

Цель данной работы — установление требований на функции /(х,г), ф(х) и у(х), при которых к задаче (1)-(3) применим классический метод Фурье. Другими словами, доказать методом Фурье существование и единственность решения смешанной задачи (1)-(3) и показать устойчивость найденного решения от данных задачи: от начальных функций и правой части уравнения (1). Аналогичные вопросы в случае когда порядок оператора А(х,О) равен двум, т.е. т — 2, былы подробно изучены в известной работе В.А. Ильина [8].

Применение метода Фурье к задаче (1)-(3) приводит нас к рассмотрению следующей спектральной задачи:

A(x,D)v(x) = Xv(x) x e Q; (4)

Bjv(x) = 0, j = 1,2. l; x e дQ. (5)

В работе С. Агмона [9] найдены достаточные условия на границу дQ области Q и на коэффициенты операторов A и Bj, обеспечивающие компактность обратного оператора, или, что тоже самое, существование полной ортонормированной в L2(Q) системы собственных функций [vk(x)> и счетного множества положительных собственных значений Xk задачи (4) — (5). Будем называть эти условия условием (A).

Применяя метод Фурье, составим следующий формальный ряд

u(x,t) = У Щ sin л/Xkt + фкcos y/Xkf + fk (%) siпл/Xk(t — %)d%] vk(x). (6)

Здесь Щк, фк и fk(t) — коэффициенты Фурье соответственно функций Щ(x), ф(x) и f (x,t) по системе собственных функций [vk(x)>, определяемые как скалярное произведение в L2(Q); например, yk = (щ,vk).

Если ряд (6) сходится равномерно и его можно достаточно число раз почленно продифференцировать и полученные ряды также сходятся равномерно, то нетрудно проверить, что функция, определенная рядом (6), является классическим решением задачи (1)-(3).

Теорема 1. (О единственности). Пусть выполнено условие (A) и пусть функции f (x,t),ф(x),щ(x) непрерывны в тех областях, которые укзаны в (1) и (2). Тогда может существовать лишь одно классическое решение смешанной задачи (1)-(3).

Всюду далее предположим, что условие (A) выполнено.

Для того, что бы сформулировать теорему о существовании нам необходимо ввести некоторые определения.

Пусть т — произвольное действительное число. В пространстве L2(Q) введем оператор Aт, действующий по правилу

Aтg(x) = У Xkgkvk(x), gk = (g, vk). k=1

Очевидно, данный оператор Aт с областью определения

D(Aт) = [g e L2(Q): £ Xf |gk|2 1 + 2m. Пусть далее ф e D(Aт), щ e D(Aт-2) и f (x, t) e D(Aт-1) при всех t e [0, T], причем функция

F (t )= A т — 2 f (x, t)

непрерывна по норме пространства L2(fí) на [0,Г]. Тогда ряд Фурье (6) можно почленно дифференцировать по переменному t до двух раз включительно а по переменным xj до m раз включительно и полученные ряды будут сходиться абсолютно и равномерно в замкнутой области Q х [0, Г].

Данная теорема в несколько иной формулировке доказана в книге М.А. Красносельского и др. [10] (см. Теорему 22.5). Из этой теоремы вытекает следующее утверждение.

Теорема 3. (О существовании). Пусть выполнены условия Теоремы 2. Тогда решение смешанной задачи (1)-(3) существует и оно представимо ввиде ряда (6).

Следует отметить, что в работе Ш.А. Алимова [11] приведены достаточные условия принадлежности заданной функции к области определения оператора A т в терминах различных классов дифференцируемых функций. Здесь мы лишь заметим, что в случае начально-краевых задач для уравнения utt + uxxxx = f(x,t), рассмотренных в работе [3], если заданные функции ф, ф и f удовлетворяют условиям теорем 2 и 5 этой работы, то условия нашей Теоремы 3 также будут выполнены. Вообще, в случае кратных тригонометрических рядов Фурье, требования Теоремы 3 являются минимальными. Именно, пусть Q совпадает N-мерным тором TN = (0,2п]N и оператор A(x,D) имеет постоянные коэффициенты и является однородным. Пусть далее, граничные условия (3) задаются условием 2п-периодичности по каждому из переменных xj и для простоты положим f(x,t) = 0. В результате получим новую смешанную задачу, которую обозначим через (TN). Для этой задачи справедливо следующее утверждение (определение пространств Соболева L2(TN) см. ниже в параграфе 4).

Теорема 4. (О существовании решения задачи (TN)). Пусть т > m + N и пусть начальные функции принадлежат соответственно пространствам Соболева: ф е

L2 (TN), у е L2 2 (TN). Тогда решение смешанной задачи (TN) существует и оно представимо ввиде абсолютно и равномерно сходящего ряда:

u(x,t)= У [ 1 yn sin vAñt + фпcos VA(ñ)t]einx, nezn VA(n)

где A(n) = У aana и yn, фп — соответствующие коэффициенты Фурье по три-

В данном случае оператор A совпадает с замыканием в L2(TN) оператора A(D) = У aaDa с периодическими условиями, а область определения оператора Ат для

любого т совпадает с пространством Соболева L£m(TN).

Возврашаясь к смешанной задачи (1)-(3), сформулируем теорему об устойчивости решения.

Теорема 5. (Об устойчивости). Пусть функции ф(x), ф(x) и f (x,t) (при любом t е [0, Г]) принадлежат в пространство L2(fí). Тогда для решения (6) задачи (1)-(3) справедлива оценка

u(x, 0) = 0, ut(x, 0) = 0, x Е О; (9)

Б]и(х,г)= У Ьа,](х)Эаи(х,г)= 0, 0 0,

ПП или, интегрируя по частям,

пк(г) = — !и(х,г)А(х,В)ук(х)(х = —Х^и(х,г)ук(х)(х = -Хкпк(г), г > 0. ПП

Учитывая начальные условия (9), заключаем, что функция ^к(г) является решением следующей задачи Коши:

^(г)+ ) = 0, г > 0; мь(0)= 4(0) = 0.

Отсюда имеем, что функция, определенная равенством (11), равна тождественно нулю: (г) = 0. Следовательно, в силу полноты ситемы собственных функций (Ук(х)>, функция и(х,г) = 0 для всех х е & и г > 0. Итак, единственность решения задачи (1)-(3) доказана.

Как было отмечено выше, Теорема 2 доказана в книге М.А. Красносельского и др. [10]. Ключевую роль в этом доказательстве играет следующая лемма, доказанная в той же работе ( [10], стр. 453):

Лемма. Пусть т > 1 + 2m• Тогда для любого |а| Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

и пусть /(х,г) удовлетворяет всем условиям Теоремы 2. Заметим, что условия на функцию /(х,г) означают равномерную по г е [0, Т] сходимость ряда

удовлетворяющее начальным условиям

и(х, 0) = ф(х), иг(х,0) = у(х), х € Т^;

и являющейся 2п-переодическим по каждому из аргументов Xj. Здесь ф(х) и у(х) также являются 2п-периодическими функциями.

Обозначим через А оператор А(О), определенный на 2п-периодических функциях из Ст(М.м). Замыкание А этого оператора в Ь2(ТМ) является самосопряженным. Оператор А имеет полную ортонормированную в Ь2(ТМ) систему собственных функций <(2п)—М/2етх>, отвечающие собственным значениям А(п), что проверяется непосредственным вычислением. Поэтому, в силу спектральной теоремы Дж. фон Неймана, для любого т > 0 оператор Ат действует по правилу Aтg(x) = £ Ат(n)gnelnx,

А(п) 0, если конечна норма

1М|(Т*) = || I (1 + |п|2)^ег’их||^)= I (1 + |п|2)аЫ2. (15)

Когда а не целое, то это пространство также называется пространством Лиувилля. Нетрудно проверить, что существуют константы С1 и С2 такие, что

С1 (1 + |п|2)тт te[0,T] 2( ) k=i Ak Ak 0

или, применяя неравенство Коши-Буняковского к последному интегралу, окончательно получим

u(x, 0) = 9(x), x E Q; (17)

и краевым условиям (3).

Теорема 7. Пусть т > N и 9(x) E D(Aт). Пусть далее f (x, t) E D(AT) при всех

г € [0, Т>, причем функция

непрерывна по норме пространства Ь2(П) на [0,Т]. Тогда существует единственное решение задачи (16), (17), (3) и оно предствимо в виде равномерно и абсолютно сходящего в замкнутой области П ряда

и(х,г) = £ [е—Хк1 фк + е—Як(г—%)fk(%)(%>ук(х), г € (0,Т], к=1 0

где фк и г) — соответствующие коэффициенты Фурье.

Данное утверждение доказывается повторением аналогичных рассуждений, приведенных выше.

Авторы приносят глубокую благодарность Ш.А. Алимову за обсуждения результатов работы.

[1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, Наука, М., 1966, 724 с. [Tikhonov A.N., Samarskiy A.A., Uravneniya matematicheskoy fiziki, Nauka, M., 1966, 724 pp.]

[2] Коренев Б. Г., Вопросы расчета балок и плит на упругом основании, Стройиздат, М., 1954, 232 с. [Korenev B.G., Voprosy rascheta balok i plit na uprugom osnovanii, Stroyizdat, M., 1954, 232 pp.]

[3] Сабитов К. Б., «Колебания балки с заделанными концами», Вест. Сам. гос. техн. унта, Сер. Физ.-мат. науки, 19:2 (2015), 311-324. [Sabitov K. B., «Kolebaniya balki s zadelannymi kontsami», Vest. Sam. gos. tekhn. un-ta, Ser. Fiz.-mat. nauki, 19:2 (2015), 311-324].

[4] Сабитов К. Б., «К теории начально-краевых задач для уравнения стержней и балок», Дифференциальные уравнения, 53:1 (2017), 89-100. [Sabitov K. B., «K teorii nachal’no-krayevykh zadach dlya uravneniya sterzhney i balok», Differentsial’nyye uravneniya, 53:1 (2017), 89-100].

[5] Сабитов К. Б., «Задача Коши для уравнения колебания балки», Дифференциальные уравнения, 53:5 (2017), 665-671. [Sabitov K. В., «Zadacha Koshi dlya uravneniya kolebaniya balki», Differentsial’nyye uravneniya, 53:5 (2017), 665-671].

[6] Касимов Ш.Г., Мадрахимов У. С., «Начально-граничная задача для уравнения колебаний балки в многомерном случае», Дифференциальные уравнения, 55:10 (2019), 1379-1391. [Kasimov SH.G., Madrakhimov U.S., «Nachal’no-granichnaya zadacha dlya uravneniya kolebaniy balki v mnogomernom sluchaye», Differentsial’nyye uravneniya, 55:10 (2019), 1379-1391].

[7] Ладыженская О. А., Смешанная задача для гиперболического уравнения, Гостехиздат, М., 1953, 281 с. [Ladyzhenskaya O.A., Smeshannaya zadacha dlya giperbolicheskogo uravneniya, Gostekhizdat, M., 1953, 281 pp.]

[8] Ильин В. А., «О разрешимости смешанных задач для гиперболического и параболического уравнений», Успехи мат. наук, 15:2 (1960), 97-154. [Il’in V. A., «O razreshimosti smeshannykh zadach dlya giperbolicheskogo i parabolicheskogo uravneniy», Uspekhi mat. nauk, 15:2 (1960), 97-154].

[9] Agmon S., «On the eigenfunctions and on the eigenvalues of general elliptic boundary value problems», Comm. Pure and Appl. Math., 15:2 (1962), 119-143.

[10] Красносельский М.А., Забрейко П. П., Пустыльник Е.И., Соболевский П. С., Интегральные операторы в пространствах суммируемых функций, Наука, М., 1966, 499 с. [Красносельский М.А., Забрейко П. П., Пустыльник Е.И., Соболевский П. С., Интегральные операторы в пространствах суммируемых функций, Наука, М., 1966, 499 pp.]

[11] Алимов Ш.А., «Дробные степени эллиптических операторов и изоморфизм классов дифференцируемых функций», Дифференциальные уравнения, 8:9 (1972), 1609-1626. [ «Drobnyye stepeni ellipticheskikh operatorov i izomorfizm klassov differentsiruyemykh funktsiy», Differentsial’nyye uravneniya, 8:9 (1972), 1609-1626].

[12] Алимов Ш.А., Ашуров Р. Р., Пулатов А. К., «Кратные ряды и интегралы Фурье. Коммутативный гармонический анализ», Итоги науки и техн. Сер. Соврем. пробл. мат. Фундам. направления, 42 (1989), 7-104. [Alimov SH.A., Ashurov R. R., Pulatov A. K., «Kratnyye ryady i integraly Fur’ye. Kommutativnyy garmonicheskiy analiz», Itogi nauki i tekhn. Ser. Sovrem. probl. mat. Fundam. napravleniya, 42 (1989), 7-104].

Список литературы (ГОСТ)

[1] Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1966. 724 с.

[2] Коренев Б. Г. Вопросы расчета балок и плит на упругом основании. М.: Стройиздат, 1954. 232 с.

[3] Сабитов К. Б. Колебания балки с заделанными концами // Вест. Сам. гос. техн. ун-та, Сер. Физ.-мат. науки. 2015. Т. 19. № 2. С. 311-324. https://doi.org/10.14498/vsgtu1406

[4] Сабитов К. Б. К теории начально-краевых задач для уравнения стержней и балок // Дифференциальные уравнения. 2017. Т. 53. № 1. С. 89-100. DOI: 10.1134/S0012266117010086

[5] Сабитов К.Б. Задача Коши для уравнения колебания балки // Дифференциальные уравнения. 2017. Т. 53. № 5. С. 665-671. DOI: 10.1134/S0012266117050093

[6] Касимов Ш. Г., Мадрахимов У. С. Начально-граничная задача для уравнения колебаний балки в многомерном случае// Дифференциальные уравнения. 2019. Т. 55. № 10. С. 1379-1391, DOI: 10.1134/S0374064119100091

[7] Ладыженская О. А. Смешанная задача для гиперболического уравнения. М.: Гостехиздат, 1953. 281 с.

[8] Ильин В. А. О разрешимости смешанных задач для гиперболического и параболического уравнений// Успехи мат. наук. 1960. Т. 15. № 2. С. 97-154.

[9] Agmon S. On the eigenfunctions and on the eigenvalues of general elliptic boundary value problems// Comm. Pure and Appl. Math. 1962. Vol. 15. issue 2. P. 119-143, https://doi.org/10.1002/cpa.3160150203

[10] Красносельский М. А., Забрейко П. П., Пустыльник Е. И., Соболевский П. С. Интегральные операторы в пространствах суммируемых функций. М.: Наука, 1966. 499 с.

[11] Алимов Ш. А. Дробные степени эллиптических операторов и изоморфизм классов дифференцируемых функций // Дифференциальные уравнения. 1972. T. 8. № 9. C. 16091626, http://mi.mathnet.ru/de1663

[12] Алимов Ш. А., Ашуров Р. Р., Пулатов А. К. Кратные ряды и интегралы Фурье. Коммутативный гармонический анализ //Итоги науки и техн. Сер. Соврем. пробл. мат. Фундам. направления, 42, ВИНИТИ. 1989. Т. 42. C. 7-104. http://mi.mathnet.ru/intf136

Для цитирования: Ашуров А. А., Мухиддинова А.Т. Начально-краевые задачи для гиперболических уравнений с эллиптическим оператором произвольного порядка // Вестник КРАУНЦ. Физ.-мат. науки. 2020. Т. 30. № 1. C. 8-19. DOI: 10.26117/2079-6641-202030-1-8-19

For citation: Ashurov R. R., Muhiddinova A. T. Initial-boundary value problem for hyperbolic equations with an arbitrary order elliptic operator, Vestnik KRAUNC. Fiz.-mat. nauki. 2020, 30: 1, 8-19. DOI: 10.26117/2079-6641-2020-30-1-8-19

Поступила в редакцию / Original article submitted: 30.03.2020

Vestnik KRAUNC. Fiz.-Mat. Nauki. 2020. vol. 30. no.1. pp. 8-19.

DOI: 10.26117/2079-6641-2020-30-1-8-19 MATHEMATICS

MSC 35G15, 35L35

INITIAL-BOUNDARY VALUE PROBLEM FOR HYPERBOLIC EQUATIONS WITH AN ARBITRARY ORDER ELLIPTIC OPERATOR

R. R. Ashurov, A. T. Muhiddinova

Institute of Mathematics named after V. I. Romanovskiy, Academy of Sciences of Uzbekistan, Academy of Sciences of Uzbekistan, Mirzo Ulugbek str., 85, Tashkent, 100170, Uzbekistan E-mail: ashurovr@gmail.com,oqila1992@mail.ru

An initial-boundary value problem for a hyperbolic equation with the most general elliptic differential operator, defined on an arbitrary bounded domain, is considered. Uniqueness, existence and stability of the classical solution of the posed problem are proved by the classical Fourier method. Sufficient conditions for the initial function and for the right-hand side of the equation are indicated, under which the corresponding Fourier series converge absolutely and uniformly. The notion of a generalized solution is introduced and existence theorem is proved. Similar results are formulated for parabolic equations too.

Key words: hyperbolic equation, initial-boundary value problems, Fourier method, existence, uniqueness, stability, classical solution, generalized solution.

Постановка задачи для уравнения гиперболического типа

Классическим примером уравнения гиперболического типа является волновое уравнение, которое имеет вид:

, 0 0 (24)

В данном случае искомая функция u(x, t) описывает малые продольные или поперечные колебания стержня или туго натянутой струны, точкам которых в начальный момент времени t =0 сообщили начальное смещение y₁(t)и скорость y₂(t). В случае продольных колебаний параметр a характеризует скорость звука в материале, из которого изготовлен стержень, а для поперечных колебаний параметр a связан с массой единицы длины струны и силой её натяжения.

Первая начально-краевая задача. Если концы стержня движутся по заданным законам, то есть на концах заданы перемещения (значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:

При постановке первой начально-краевой задачи для волнового уравнения условием (28) задаётся начальное распределения значений искомой функции u(x, t) (характеризующей смещение точек стрежня или струны), а условием (29) задаётся ещё и начальная скорость такого смещения.

Вторая начально-краевая задача. Если на концах стержня заданы значения силы, которая по закону Гука пропорциональна производной перемещения по пространственной переменной (т.е. на концах заданы значения первых производных по пространственной переменной x), то ставится вторая начально-краевая задача для волнового уравнения:

В условиях, когда концы стержня свободны, то функции j ₁(t) = j ₂(t) = 0.

Третья начально-краевая задача. Если концы стержня или струны закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, то ставится третья начально-краевая задача для волнового уравнения

Аналогично ставятся двумерные трехмерные начально-краевые задачи для двумерного и трёхмерного волнового уравнения.

Замечание. Необходимо отметить, что волновое уравнение (24) легко трансформируется в систему уравнений акустики (13), являющихся простейшей линейной моделью газодинамических течений. Действительно, введём следующие обозначения:

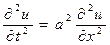
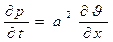
Продифференцируем уравнение (30) по переменной t, а уравнение (31) по переменной x и подставим результат в волновое уравнение , при этом получим:

(32)

Далее продифференцируем уравнение (30) по переменной x, а уравнение (31) по переменной t ,в результате будем иметь:

и

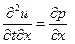
Полагая далее, что смешанные производные от u(x, t) по переменным x и t не зависят от порядка дифференцирования, получим:

(33)

Полученную систему уравнений (32), (33):

называют уравнениями акустики, как уже отмечалось выше, функции p и J характеризуют возмущения (т.е. слабые колебания) давления и скорости в акустической волне.