Решение нелинейные уравнения второго порядка

Решение нелинейные уравнения второго порядка

Мир математических уравнений

Точные решения > Обыкновенные дифференциальные уравнения > Нелинейные обыкновенные дифференциальные уравнения второго порядка

3. Нелинейные обыкновенные дифференциальные уравнения второго порядка

3.1. Дифференциальные уравнения вида y′′ = f(x, y)

1. y′′ = f(y). Автономное уравнение.
2. y′′ = Ax n y m . Уравнение Эмдена—Фаулера.
3. y′′ + f(x)y = ay −3 . Уравнение Ермакова.
4. y′′ = f(ay + bx + c).
5. y′′ = f(y + ax 2 + bx + c).
6. y′′ = x −1 f(yx −1 ). Однородное уравнение.
7. y′′ = x −3 f(yx −1 ).
8. y′′ = x −3/2 f(yx −1/2 ).
9. y′′ = xk−2 f(x −k y). Обобщенно-однородное уравнение.
10. y′′ = yx −2 f(x n y m ). Обобщенно-однородное уравнение.
11. y′′ = y −3 f(y(ax 2 + bx + c) −1/2 ).
12. y′′ = e −ax f(e ax y).
13. y′′ = yf(e ax y m ).
14. y′′ = x −2 f(x n e ay ).
15. y′′ = (ψ′′/ψ)y + ψ −3 f(y/ψ), ψ = ψ(x).

3.2. Дифференциальные уравнения вида f(x, y)y′′ = g(x, y, y′)

1. y′′ − y′ = f(y). Автономное уравнение.
2. y′′ + f(y)y′ + g(y) = 0. Уравнение Льенарда.
3. y′′ + [ay + f(x)]y′ + f′(x)y = 0.
4. y′′ + [2ay + f(x)]y′ + af(x)y 2 = g(x).
5. y′′ = ay′ + e 2axf(y).
6. y′′ = f(y)y′.
7. y′′ = [e αxf(y) + α]y′.
8. xy′′ = ny′ + x 2n + 1 f(y).
9. xy′′ = f(y)y′.
10. xy′′ = [x k f(y) + k − 1]y′.
11. x 2 y′′ + xy′ = f(y).
12. (ax 2 + b)y′′ + axy′ + f(y) = 0.
13. y′′ = f(y)y′ + g(x).
14. xy′′ + (n + 1)y′ = xn − 1 f(yx n ).
15. g(x)y′′ + 1/2 g′(x)y′ = f(y).
16. y′′ = −ay′ + e ax f(ye ax ).
17. xy′′ = f(x n e ay )y′.
18. x 2 y′′ + xy′ = f(x n e ay ).
19. yy′′ + (y′) 2 + f(x)yy′ + g(x) = 0.
20. yy′′ − (y′) 2 + f(x)yy′ + g(x)y 2 = 0.
21. yy′′ − n(y′) 2 + f(x)y 2 + ay 4n − 2 = 0.
22. yy′′ − n(y′) 2 + f(x)y 2 + g(x)yn + 1 = 0.
23. yy′′ + a(y′) 2 + f(x)yy′ + g(x)y 2 = 0.
24. yy′′ = f(x)(y′) 2 .
25. y′′ − a(y′) 2 + f(x)e ay + g(x) = 0.
26. y′′ − a(y′) 2 + be 4ay + f(x) = 0.
27. y′′ + a(y′) 2 − 1/2 y′ = e x f(y).
28. y′′ + α(y′) 2 = [e βxf(y) + β]y′.
29. y′′ + f(y)(y′) 2 + g(y) = 0.
30. y′′ + f(y)(y′) 2 − 1/2 y′ = e x g(y).
31. y′′ = xf(y)(y′) 3 .
32. y′′ = f(y)(y′) 2 + g(x)y′.
33. y′′ = f(x)g(xy′ − y).
34. y′′ = yx −2 f(xy′/y).
35. gy′′ + 1/2 g′y′ = f(y)h(y′g 1/2 ), g = g(x).
36. y′′ = f((y′) 2 + ay).

Веб-сайт EqWorld содержит обширную информацию о решениях различных классов обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, интегральных уравнений, функциональных уравнений и других математических уравнений.

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

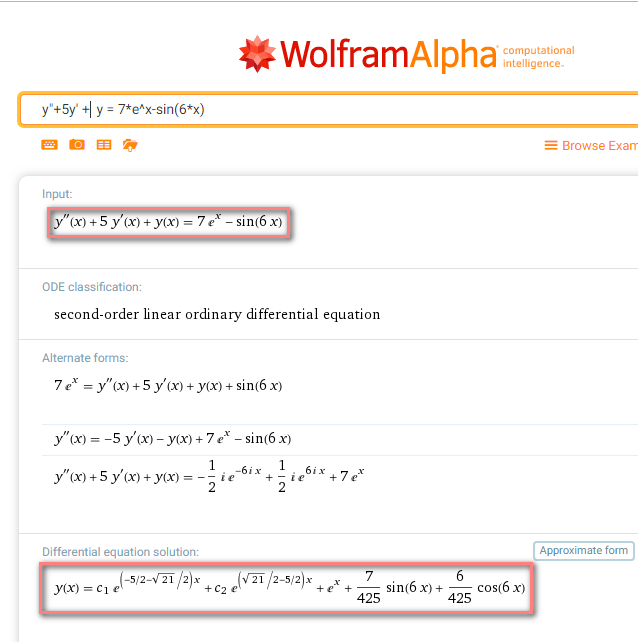
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x \quad (x \ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, \, y(1/3)=1, \, y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= \frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+\cos x, \quad y(0)=0, y'(0)=0, y»(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

Нелинейное уравнение второго порядка и линейное уравнение третьего порядка Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Чочиев Т.З.

В работе решаются нелинейное уравнение второго порядка и связанное с ним линейное уравнение третьего порядка методом последовательного понижения порядка производной.

Похожие темы научных работ по математике , автор научной работы — Чочиев Т.З.

SECOND — ORDER NONLINEAR EQUATION AND THIRD — ORDER LINEAR EQUATION

In this paper, a second-order nonlinear equation and a third-order linear equation with it are solved by the method of successively decreasing the order of the derivative.

Текст научной работы на тему «Нелинейное уравнение второго порядка и линейное уравнение третьего порядка»

Europe» (Praha, Czech Republic) / 2017/ — № 13 (13), vol 2 — p. 28-37.

3. Рысин А.В, Рысин О.В, Бойкачев В.Н, Никифоров И.К. Математическое обоснование философских законов теории мироздания // Науч. журнал » Sciences of Europe» (Praha, Czech Republic) / 2017/ -№ 14 (14), vol 1 — p. 99-108.

4. Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. — М.: Наука, 1979, С. 60.

5. Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. — М.: Наука, 1979, С. 30.

6. Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. — М.: Наука, 1979, С. 58.

7. Рысин А.В., Рысин О.В., Бойкачев В.Н., Никифоров И.К. Переход от усовершенствованных уравнений Максвелла к уравнению движения частицы // Ежемесячный науч. журнал: Национальная ассоциация ученых. ч. 2. — 2014. — № 5. — С. 99-107.

8. Рысин А.В, Рысин О.В, Бойкачев В.Н, Никифоров И.К. Иерархия мироздания и математическое получение константы в усовершенствованных уравнениях Максвелла // Науч. журнал » Sciences of

Europe» (Praha, Czech Republic) / 2016/ — № 10 (10), vol 2 — p. 73-85.

9. Рысин А.В, Рысин О.В, Бойкачев В.Н, Никифоров И.К. Парадоксы мюонных и электронных нейтрино и антинейтрино и уравнений Дирака в квантовой механике // Науч. журнал » Sciences of Europe» (Praha, Czech Republic) / 2017/ — № 17 (17), vol 2 — p. 67-75.

10. Терлецкий Я.П., Рыбаков Ю.П. Электродинамика — М: Высш. шк., 1980. С. 226.

11. Рысин А.В, Рысин О.В, Бойкачев В.Н, Никифоров И.К. Вывод соотношения масс протона и электрона на основе логики мироздания и термодинамического равновесия // Науч. журнал » Sciences of Europe» (Praha, Czech Republic) / 2017/ — № 19 (19), vol 1 — p. 41-47.

12. Савельев И.В. Курс общей физики, т. 3. -М.: Наука, 1979. С. 34.

13. Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. — М.: Наука, 1979. С. 312.

14. Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. — М.: Наука, 1979. С. 42.

НЕЛИНЕЙНОЕ УРАВНЕНИЕ ВТОРОГО ПОРЯДКА И ЛИНЕЙНОЕ УРАВНЕНИЕ ТРЕТЬЕГО ПОРЯДКА

профессор Юго-Осетинского государственного университета, кандидат физико-математических наук, г. Цхинвал

SECOND — ORDER NONLINEAR EQUATION AND THIRD -ORDER LINEAR EQUATION

professor of South Ossetian State University, candidate of physical and mathematical sciences, Tskhinval АННОТАЦИЯ

В работе решаются нелинейное уравнение второго порядка и связанное с ним линейное уравнение третьего порядка методом последовательного понижения порядка производной. ABSTRACT

In this paper, a second-order nonlinear equation and a third-order linear equation with it are solved by the method of successively decreasing the order of the derivative.

Ключевые слова: нелинейность, решение, порядок, последовательное понижение порядка, класс Риккати, выполнимость, линейность.

Keywords: nonlinearity, solution, order, sequential reduction of order, Riccati class, feasibility, linearity.

П1. Линейное уравнение третьего порядка

Известно, что решение любого линейного уравнения порядка выше первого тесно связано с решением нелинейного уравнения, порядка на единицу ниже [2], которое назвали сопровождающим нелинейным уравнением линейного уравнения.

В настоящем имеем своей целью исследовать линейное уравнение третьего порядка.

у»’ + А(х)у» + В(х)у’ + С(х)у = f[x), 0 )dx] = 0.

z’o — z2 + Az0- В = C0e-So(A-Zo)dx’ (2.3)

где C0 постоянная. Отсюда непосредственно устанавливается,

(e- ¡oXzodx)» + A(e- Soi^*)’ + Be— oia^dx ). (2.6)

^ (y1 + C0 J e- foX(A-1o)dx dx),

F(x) = e- -o >odx IY1 + C0 I e- -o (A-1o)dx dx),

у1 и у2 постоянные; при х = 0, у1 = Р(0), у2 = 1; но из (2.6) F1(0) = 1(0)—z0(0). Формула (2.6)

определяет функцию z0, удовлетворяющую нелинейному уравнению (2.2).

Вернемся к уравнению (2.1).

Если С(х) = 0, то оно совпадает с (2.2), которое удовлетворяет. Чтобы z0, определенная из (2.6), удовлетворяло и уравнению (2.1), применяем известный прием Лагранжа, называемый вариацией постоянного; то есть, считая в (2.3) С0 = С0(х) и подставив ее в уравнение (2.1) для С0(х) получим:

С0(х) = (у1 — /* С(х)е£(л-г)ах йх). (2.7)

8аепсе8 of Бигоре # 27, (2018)

l’0-z2+Az0-B = е-^-^ (у1-1 С(х)е^оХ(А-2)ах ах

Если С(х) = 0, то z = z0 и (2.3) выполняется тождественно; если же С(х) Ф 0, то (2.8) удовлетворяет уравнению (2.1). Но тут вызывает неудобство, то что в правой части содержится неизвестная z (у1 -постоянная), которую нужно определить.

Не будет ограничением, если ее зададим в форме

где а(х) неизвестная. Подставим это значение в (2.1) и в правую часть (2.8). После очевидной группировки придем к следующим двум равенствам: