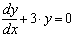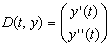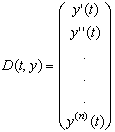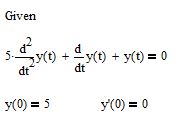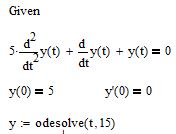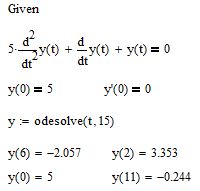Решение нелинейных дифференциальных уравнений на mathcad
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
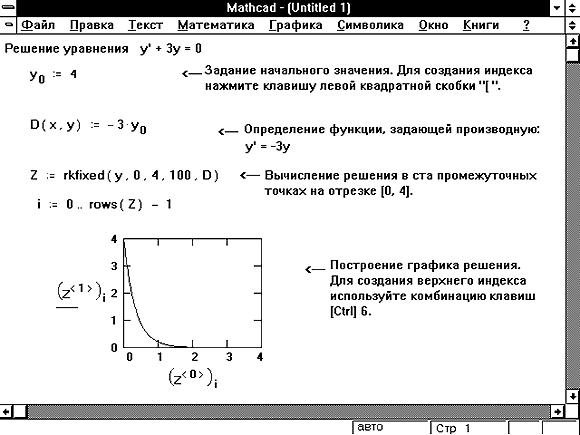
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
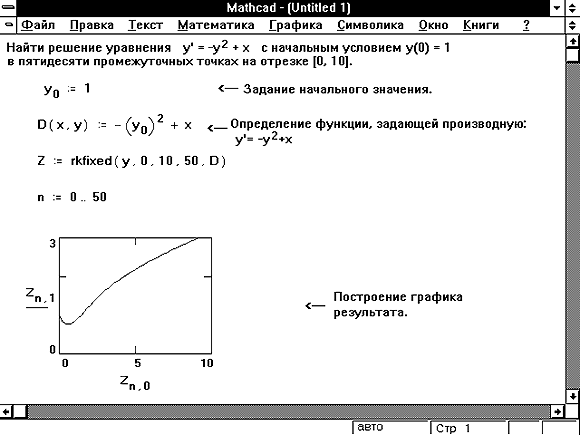
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение дифференциальных уравнений в MathCad 15
В статье рассмотрена работа функции odesolve для графического решения дифференциального уравнения в программе mathcad версии 15 и старше
Функция odesolve
Для примера рассмотрим простейшее дифференциальное уравнение, описывающее затухающие колебания маятника с течением времени
В свободном поле mathcad введите оператор Given. Этот оператор запускает процесс ввода исходных данных для корректной работы функции odesolve. После этого найдите панель под названием Calculus. В этой панели нам понадобятся кнопки Derivative и Nth Derivative. Эти кнопки вводят заготовки для дифференциального уравнения. С помощью клавиатуры введите уравнение, как показано на рисунке 1. Знак равенства необходимо использовать из панели Boolean
Рис. 1. Ввод исходных данных для решения дифференциального уравнения
Далее введите начальные приближения. Количество начальных приближений зависит от порядка дифференциального уравнения. В нашем случае их будет 2. Введите приближения, как показано на рисунке 2. Обратите внимание, что для ввода значания первой производной вам нужно использовать символ «верхний апостроф«. Если вы его не можете ввести с клавиатуры вручную воспользуйтесь приложением windows Capter Map или используйте комбинацию клавиш Alt + 96 или Alt + 39
Рис. 2. Ввод первого приближения для решения дифференциального уравнения
Теперь, после начального приближения введите любую переменную (например y) и присвойте ей функцию Odesolve, как показано на рисунке 3. В качестве параметров функции Odesolve используется переменная t и интервал интегрирования. В нашем случае интервал равен 15
Рис. 3. Ввод функции odesolve для решения дифференциального уравнения
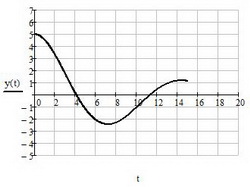
Можно отобразить функцию y на графике, где в качестве аргумента будет переменная t. Этот график и будет являться решением дифференциального уравнения. Обратите внимание, что график строится в пределах интервала интегрирования. Особенности оформления и отображения графиков в mathcad 15 смотрите в соответствующем разделе
Рис. 4. Вывод результата решения дифференциального уравнения на график
После корректного решения дифференциального уравнения функцию y(t) можно использовать далее в расчетах
Рис. 5. Результат решения дифференциального уравнения в mathcad 15 и старше
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
Rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции Rkfixed с указанием параметров функции.
Y – вектор начальных условий из K элементов (k – количество уравнений в системе);
X1 и X2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
P – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из K-Элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD.
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y1, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора Y, границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица Z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора V, и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица S, в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции Rkfixed. Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью Rkfixed
Для решения уравнения с помощью функции Rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора А, построены графики исходной функции, функций первой и второй производных.
http://student-engineer.pro/mathcadold/difur/
http://matica.org.ua/metodichki-i-knigi-po-matematike/reshenie-zadach-v-srede-mathcad/28-tema-7-reshenie-differentcialnykh-uravnenii-i-sistem-v-mathcad-kratkie-teoreticheskie-svedeniia