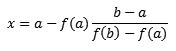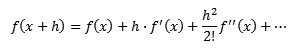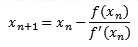Решение нелинейных уравнений на языке программирования Pascal
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.
Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.
Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.
Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:
После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.
Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.
В основе метода Ньютона лежит разложения функции в ряд Тейлора:
Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.
Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:
Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.
Программа для метода бисекции
Дана функция f (x) с плавающим числом x и двумя числами «a» и «b» такая, что f (a) * f (b) 3 + a 2 x 2 +… .. + e, где aa 1 , a 2 ,… — константы, а x — переменная ,
Трансцендентальной функцией являются неалгебраические функции, например, f (x) = sin (x) * x — 3 или f (x) = e x + x 2 или f (x) = ln (x) + x….
Что такое метод деления пополам?
Этот метод также называется методом деления пополам, методом двоичного поиска или методом дихотомии. Этот метод используется, чтобы найти корень уравнения в заданном интервале, который является значением «x», для которого f (x) = 0.
Метод основан на теореме о промежуточном значении, которая гласит, что если f (x) — непрерывная функция и существуют два действительных числа a и b, такие что f (a) * f (b) 0 и f (b) 
Ниже приведена реализация вышеуказанных шагов.
// C ++ программа для реализации метода Bisection для
// решение уравнений
#include
using namespace std;
#define EPSILON 0.01
// Пример функции, решение которой определяется с помощью
// Метод деления пополам. Функция х ^ 3 — х ^ 2 + 2
double func( double x)
return x*x*x — x*x + 2;
// Печатает корень функции func (x) с ошибкой EPSILON
void bisection( double a, double b)
if (func(a) * func(b) >= 0)
cout «You have not assumed right a and b\n» ;
while ((b-a) >= EPSILON)
// Найти среднюю точку
// Проверяем, является ли средняя точка корневой
// Определим сторону, чтобы повторить шаги
else if (func(c)*func(a)
cout «The value of root is : «
// Программа драйвера для проверки вышеуказанной функции
// Предполагаемые начальные значения
double a =-200, b = 300;
// Java-программа для реализации метода Bisection
// для решения уравнений
static final float EPSILON = ( float ) 0.01 ;
// Пример функции, решение которой определяется с помощью
// Метод деления пополам. Функция х ^ 3 — х ^ 2 + 2
static double func( double x)
return x*x*x — x*x + 2 ;
// Печатает корень функции func (x) с ошибкой EPSILON
static void bisection( double a, double b)
if (func(a) * func(b) >= 0 )
System.out.println( «You have not assumed»
while ((b-a) >= EPSILON)
// Найти среднюю точку
// Проверяем, является ли средняя точка корневой
// Определим сторону, чтобы повторить шаги
else if (func(c)*func(a) 0 )
// выводит значение c до 4 десятичных знаков
System.out.printf( «The value of root is : %.4f»
// Программа драйвера для проверки вышеуказанной функции
public static void main(String[] args)
// Предполагаемые начальные значения
double a =- 200 , b = 300 ;
// Этот код предоставлен Нирмал Патель
# Python программа для реализации
Метод деления пополам
# решение уравнений
# Пример функции, чья
# решение определяется с помощью
Метод деления пополам.
# Функция x ^ 3 — x ^ 2 + 2
return x * x * x — x * x + 2
# Печатает корень функции (x)
# с ошибкой EPSILON
if (func(a) * func(b) > = 0 ):
print ( «You have not assumed right a and b\n» )
while ((b — a) > = 0.01 ):
# Найти среднюю точку
# Проверьте, является ли средняя точка корневой
# Решите сторону повторить шаги
if (func(c) * func(a) 0 ):
print ( «The value of root is : » , «%.4f» % c)
# Код драйвера
# Предполагаемые начальные значения
# Этот код добавлен
# Анант Агарвал.
// C # программа для реализации
// Метод деления пополам
// решение уравнений
static float EPSILON = ( float )0.01;
// Пример функции, чья
// решение определяется с помощью
// Метод деления пополам. Функция
// это х ^ 3 — х ^ 2 + 2
static double func( double x)
// Печатает корень функции func (x)
// с ошибкой EPSILON
static void bisection( double a,
if (func(a) * func(b) >= 0)
Console.WriteLine( «You have not assumed» +
while ((b — a) >= EPSILON)
// Найти среднюю точку
// точка является корнем
else if (func(c) * func(a)
// выводит значение c
// до 4 десятичных знаков
Console.WriteLine( «The value of » +
static public void Main ()
// Предполагаемые начальные значения
double a = -200, b = 300;
// Этот код предоставлен ajit
// PHP программа для реализации
// Метод деления пополам
// уравнения
// Пример функции, чья
// решение определено
// используя метод деления пополам.
// Функция x ^ 3 — x ^ 2 + 2
function func( $x )
// Печатает корень функции func (x)
// с ошибкой EPSILON
function bisection( $a , $b )
echo «You have not assumed » .
«right a and b» , «\n» ;
while (( $b — $a ) >= $EPSILON )
// Найти среднюю точку
// точка является корнем
else if (func( $c ) * func( $a )
echo «The value of root is : » , $c ;
// Предполагаемые начальные значения
// Этот код предоставлен ajit
?>
Выход:
Временная сложность: — Временная сложность этого метода зависит от предполагаемых значений и функции.
Какие плюсы и минусы?
Преимущество метода деления пополам состоит в том, что он гарантированно сходится. Недостатком метода деления пополам является то, что он не может обнаружить несколько корней.
В целом, метод деления пополам используется для получения начального грубого приближения решения. Затем более быстрые методы сходятся, чтобы найти решение.
Вскоре мы обсудим другие методы решения алгебраических и трансцендентных уравнений.
Эта статья предоставлена Абхираджем Смитом . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме
Лабораторная работа 8. Численное решение нелинейных уравнений
Цель работы: Изучение методов численного решения нелинейных уравнений — методов бисекции, хорд, простой итерации, релаксации, метода Ньютона и его модификаций; исследование скорости сходимости итерационных процедур; изучение метода Эйткена ускорения сходимости; сравнение числа итераций, необходимого для достижения заданной точности вычисления разными методами.
8.1 Краткие теоретические сведения
Численное решение нелинейного уравнения F(x)=0 заключается в вычислении с заданной точностью значения всех или некоторых корней уравнения и распадается на несколько задач: во-первых, надо исследовать количество и характер корней (вещественные или комплексные, простые или кратные), Во-вторых, определить их приближенное расположение, т. е. значения начала и конца отрезка, на котором лежит только один корень, В-третьих, выбрать интересующие нас корни и вычислить их с требуемой точностью. Вторая задача называется Отделением корней. Решив ее, по сути дела, находят приближенные значения корней с погрешностью, не превосходящей длины отрезка, содержащего корень. Отметим два простых приема отделения действительных корней уравнения — табличный и Графический. Первый прием состоит в вычислении таблицы значений функции F(x) В заданных точках Xi и использовании следующих теорем математического анализа:
1. Если функция Y=f(x) непрерывна на отрезке [а, b] и f(a)f(b) 0, то последовательные приближения сходятся к корню монотонно.
Метод релаксации — один из вариантов метода простой итерации:
.
Если функция F(x) отрицательная, то рассматривают уравнение Y= — f(x). Метод имеет линейную скорость сходимости.
Метод Ньютона (касательных). Для начала вычислений требуется задание одного начального приближения X0, последующие приближения вычисляются по формуле
.
Метод имеет квадратичную скорость сходимости для простого корня, но очень чувствителен к выбору начального приближения. При произвольном начальном приближении итерации сходятся, если всюду 
, в противном случае сходимость будет только при X0, достаточно близком к корню. Существует несколько достаточных условий сходимости. Если производные F'(X) и f»(X) Сохраняют знак в окрестности корня, рекомендуется выбирать X0 так, чтобы 
. Если, кроме этого, для отрезка [А, b], содержащего корень, выполняются условия
То метод сходится для любых X0 Î[А, b]. При вычислении кратного корня производная F'(X) близка к нулю в окрестности корня, и сходимость метода замедляется.
Модифицированный метод Ньютона применяют, если хотят избежать многократного вычисления производной:
.
Метод имеет линейную скорость сходимости.
Метод секущих Получают из метода Ньютона заменой производной F'(X), разделенной разностью, вычисленной по известным значениям Xn И Xn-1:
.
Метод является двухшаговым, его порядок сходимости a»1.618, что хуже, чем в методе Ньютона. Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих — только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать больше итераций и получить более высокую точность.
Метод Эйткена ускорения сходимости. Главным является требование Линейной сходимости основного итерационного метода. В случае методов, имеющих более высокую скорость сходимости, ускорение по Эйткену неэффективно. Метод состоит в том, что после вычисления Xn, Xn+1 И Xn+2 производится пересчет по формуле
И значение yN+1 принимается за новое приближение. Оно дает лучшее приближение к корню, чем очередная итерация Xn+2. На практике не обязательно проводить пересчет на каждой итерации. Обычно он осуществляется циклически, т. е. через определенное число основных итераций.
С помощью метода Эйткена на основе известных итерационных методов получены новые, обладающие более высокой сходимостью.
Метод Вегстейна — улучшенный по Эйткену метод простой итерации; — записан в виде, позволяющем проверять целесообразность пересчета:
.
Если Rn почти постоянны, то использование в качестве очередного приближения YN+1 сильно ускорит сходимость. Итерации прекращают, если выполняется
.
Метод Стеффенсена имеет квадратичную сходимость, — более быструю, чем исходный метод релаксации:
.
8.2 Описание работы
1. Напишите программу, решающую нелинейное уравнение тремя методами (по выбору преподавателя). Предусмотрите в программе подсчет числа итераций, необходимого для достижения заданной точности e вычисления корня каждым методом.
2. Вычислите корни нечетной кратности уравнения, используя один из безусловно сходящихся методов с точностью E ( E = 10-4, 10-5, 10-6).
3. Примените метод простой итерации для нахождения одного из корней с точностью E ( E = 10-4, 10-5, 10-6) при различных начальных приближениях.
4. Вычислите все корни уравнения, используя метод Ньютона или одну из модификаций с точностью E ( E = 10-4, 10-5, 10-6) при различных начальных приближениях.
5. Примените метод Эйткена ускорения сходимости к используемым методам и исследуйте его влияние на число итераций.
8.3 Содержание отчета
1. Название и цель работы.
2. Исходная постановка задачи.
3. Результаты вычислений корней уравнения тремя методами с заданной точностью при различных начальных приближениях.
4. Результаты исследования зависимости числа итераций от требуемой точности и используемого метода.
http://espressocode.top/program-for-bisection-method/
http://naparah.com/programmirovanie/07141248.html