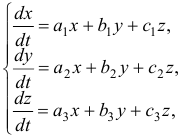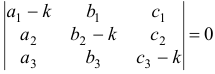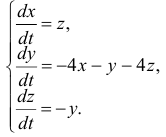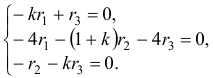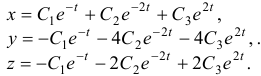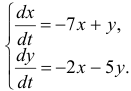Решение неоднородной системы уравнений с помощью характеристического уравнения

Решение систем дифференциальных уравнений с помощью характеристического уравнения

Пусть дана однородная система

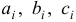
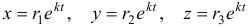
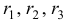
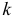
где — постоянные. Будем искать частные решения системы в виде , где и — неопределенные коэффициенты, которые следует найти. Уравнение

называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты .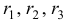

Пример №1

Найти общее решение системы

Решение:

Система в данном случае имеет вид:

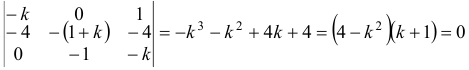
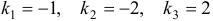
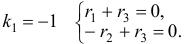
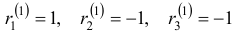
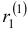
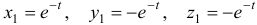
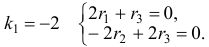
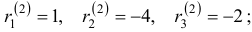
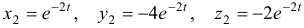
Характеристическое уравнение имеет корни . Для Решением этой системы будут, например, числа (здесь выбрано произвольно). Следовательно, . Для Решая эту систему, получим тогда .

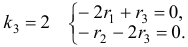
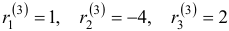
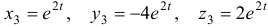
Наконец, для Здесь можно положить и будем иметь .

Общее решение данной системы дифференциальных уравнений таково:

Пример №2

Решение:

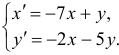
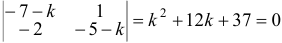
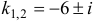
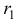
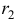
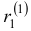
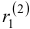
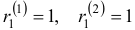
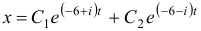
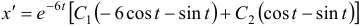
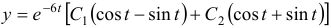
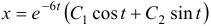
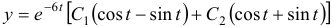
Чаще системы дифференциальных уравнений записывают в виде: Составим характеристическое уравнение и найдем его корни . Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел и . В этом случае, учитывая возможность произвольного выбора и , целесообразно сразу положить и, записав функцию или, что то же самое, , найти функцию , используя первое уравнение системы: . Для этого найдем или . Подставляя и в первое уравнение системы, получим . Общим решением системы будет и .

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Решение неоднородной системы уравнений с помощью характеристического уравнения

Пусть задана неоднородная система линейных алгебраических уравнений размерности m × n .

Матрица называется расширенной матрицей системы, если наряду с коэффициентами при неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m × (n+1) .

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса , который основан на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае преобразования производятся по столбцам).

Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.

На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.

Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.

Если r = n , то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы .

Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.

1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:

2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов переменных системы (1.10) равно числу сочетаний из n элементов по r элементов C_n r . Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно C_n r .

Пусть строки матрицы обозначены соответственно l ₁ ; l ₂ ;…; l_n . Строка l называется линейной комбинацией строк l ₁ ; l ₂ ;…; l_n матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть , .

Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных ( r n ) . В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:

Так как r ( A ) =2 и , то по теореме 1.3 (Кронекера-Капелли) заданная система линейных алгебраических уравнений совместна. Количество переменных n =2 , т.е. r n , значит, система является неопределённой. Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов переменных: < x ₁ ; x ₂ >, < x ₁ ; x ₃ >, < x ₁ ; x ₄ >, < x ₂ ; x ₃ >, < x ₂ ; x ₄ >, < x ₃ ; x ₄ > . Рассмотрим один из них < x ₁ ; x ₂ > . Тогда систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

По формулам (1.6) имеем

Данное выражение базисных переменных через свободные представляет собой общее решение системы:

При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x ₃ = x ₄ = 17 . При x₃=0 x₄=0 получаем базисное решение системы

Линейные неоднородные системы дифференциальных уравнений

Неоднородную систему дифуравнений обычно представляют в следующем виде:

В отличие от однородной системы, здесь в каждом уравнении добавляется некая функция, которая зависит от t. Функции f(t) и g(t) могут быть как const, exp, так и sin, cos и т.д.

Необходимо найти частное решение системы линейных дифуравнений
при начальных условиях x(0) = 6, y(0) = 5.

Итак, у нас есть линейная неоднородная система дифуравнений, где в качестве f(t) и g(t) выступают константы. Будем использовать метод исключения.

Выразим из первого уравнения системы:

Опять применим маркер * для выделения.

Обе части уравнения дифференцируем по t:

Производная const = 0, поэтому 3 исчезла.

Подставляем и во второе уравнение системы:

Избавимся от дробей, для чего обе части уравнения умножим на 5:

Итак, мы получили линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Этим и отличается наше решение от решения однородной системы уравнений.

Но иногда, отметим, в неоднородной системе может получиться и однородное уравнение.

Находим общее решение однородного уравнения

Для этого необходимо составить и решить характеристическое уравнение:

– мы нашли сопряженные комплексные корни, поэтому:

.

Теперь займемся поиском частного решения неоднородного уравнения вида .

Находим первую и вторую производную:

Подставляем в левую часть неоднородного уравнения:

Получаем:

Это частное решение можно с легкостью подобрать устно и можно просто записать: «Очевидно, что частное решение неоднородного уравнения: ».

В итоге:

Найдем функцию y(t).

Для этого найдем производную от найденной функции x(t):

Подставляем и в уравнение (*):

Получаем общее решение системы:

Теперь найдем частное решение, соответствующее начальным условиям x(0) = 6, y(0) = 5:

Ответ: частное решение:

Метод характеристического уравнения (метод Эйлера)

Этот метод используется крайне редко, но мы все-же рассмотрим его на примере.

Дается линейная однородная система дифуравнений

Требуется отыскать общее решение системы уравнений методом Эйлера.

Составим определитель второго порядка:

Далее надо составить характеристическое уравнение, для чего из каждого числа, расположенного на главной диагонали, вычтем некий параметр k:

Получили квадратное уравнение. Найдем его корни:

В случае, когда характеристическое уравнение имеет 2 различных действительных корня, общее решение системы дифференциальных уравнений будет иметь вид:

Коэффициенты в показателях экспонент мы уже нашли, займемся поиском коэффициентов

Подставим корень в характеристическое уравнение:

Составим систему двух линейных уравнений из чисел определителя:

Из которой получаем:

Подберем наименьшее значение , при котором будет целым. Очевидней всего будет =5, тогда =7/5*5 = 7.

Подставим корень в характеристическое уравнение:

Составим систему двух линейных уравнений из чисел определителя:

Из которой получаем:

Подберем наименьшее значение , при котором будет целым. Очевидней всего будет .

Коэффициенты найдены, подставляем их в систему

Ответ: общее решение:

Chanel Allure (http://духи.рф/catalog/men/Chanel/Allure)
Есть много имен — женские имена русские (http://духи.рф/catalog/men/Chanel/Allure) поражают своей красотой и разнообразием.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: