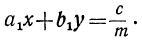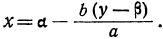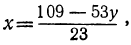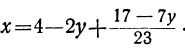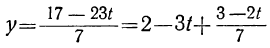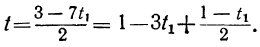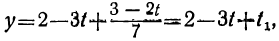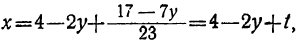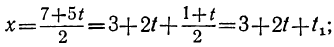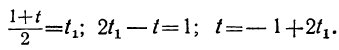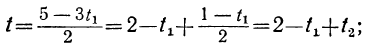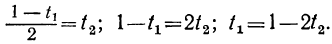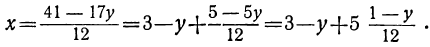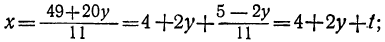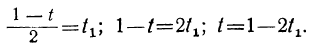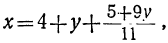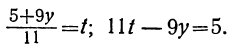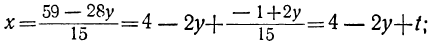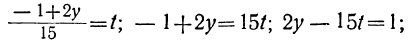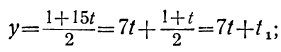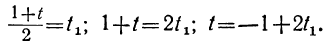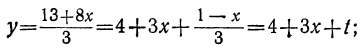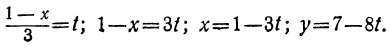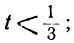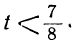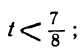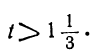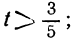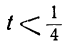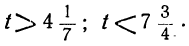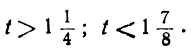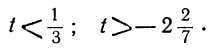Неопределенные уравнения в математике с примерами решения и образцами выполнения
При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.
Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.
Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.
Задача:
Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.
Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.
Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).
Задача:
Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?
Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.
Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.
Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.
Признак невозможности решения уравнения в целых числах
Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.
Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.
Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.
Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.
Разделив все его члены на m, получим:
При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.
Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.
Признак невозможности решения уравнения в положительных числах
Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.
Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.
Общая формула корней неопределённого уравнения
Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.
Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.
Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или
Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
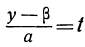
Подставляя в формулу для х число t вместо дроби 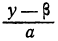
x = a-bt.
Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.
Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.
Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:
- Первым членом формулы является найденное частное значение данного неизвестного.
- Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
- Один из коэффициентов берётся с обратным знаком.
Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.
Пример:
Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.
Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:
| t | 0 | 1 | 2 | 3 | -1 | -2 | … |
| x | 2 | 7 | 12 | 17 | -3 | -8 | … |
| y | 4 | 1 | -2 | -5 | 7 | 10 | … |
Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.
Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.
Способ подстановки
Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.
Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения
Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.
Очевидно, что любому целому значению у будет соответствовать целое же значение х.
Пример:
Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:
| x | 0 | 1 | 2 | 3 | 4 | -1 | -2 | … |
| y | 18 | 13 | 8 | 3 | -2 | 23 | 28 | … |
Общее решение неопределённого уравнения
Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.
Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:
или, исключив целую часть:
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение 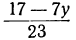
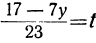
Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 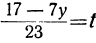
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.
По отношению к новому уравнению поступаем таким же образом. Определяем из него у:
Для того чтобы у было целым, необходимо и достаточно, чтобы 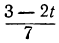
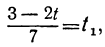
При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:
Приравняв выражение 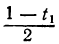
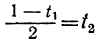
Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.
Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: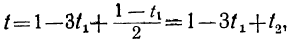
получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:
получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:
получим соответствующие целые значения для х.
Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .
Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.
Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .
Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.
Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:
| t₂ | 0 | 1 | 2 | -1 | -2 |
| x | -16 | 37 | 90 | -69 | -122 |
| y | 9 | -14 | -37 | 32 | 55 |
Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:
- Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.
- Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.
- Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.
Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.
Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:
Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.
Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.
1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.
Пример:
Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.
Решаем последнее уравнение:
Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .
Пример:
Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.
Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.
Решаем последнее уравнение:
Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .
2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.
Пример:
Дано уравнение: 12x+17y=41.
Решаем его относительно х:
Для того чтобы выражение 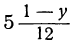
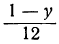
Приравнивая это выражение целому числу t, получим: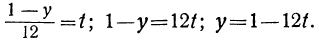
Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t
3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.
Пример:
Дано уравнение: 11х—20y=49.
Решим его относительно х:
Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.
Если бы решали данное уравнение обычным способом, то получили бы для х:
и следующее уравнение было бы:
Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.
Пример:
Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:
Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.
Положительные решения
Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.
Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.
Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.
1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
bt > — a ; at 0; 2+-5t>0,
или
Взяв для t любое целое число, большее 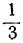
Пример:
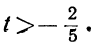
Решаем уравнение:
Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или
Любое целое значение t, меньшее 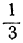
2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:
Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.
Пример:
4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или
Неравенства противоречат друг другу; уравнение не имеет положительных решений.
3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:
Все целые значения t, заключающиеся между 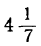
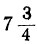
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:
Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.
Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:
Неравенства не противоречат друг другу, но между 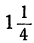
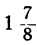
находится ни одного целого числа. Уравнение не имеет целых положительных решений.
Пример:
3x+7y=55.
Решаем уравнение: 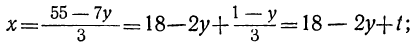
у=1 — 3t; x= 16+7t.
Отсюда:
1 —3t>0; 16+7t> 0,
или
Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:
| t | 0 | -1 | -2 |
| x | 16 | 9 | 2 |
| y | 1 | 4 | 7 |
Пример:
5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
Отсюда:
Неравенства не противоречат друг другу; но между 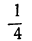
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Из опыта работы учителя математики Ханиной Марины Федоровны «Методы решения неопределенных уравнений»
Муниципальное бюджетное образовательное учреждение
Из опыта работы
учителя математики Ханиной Марины Федоровны
Методы решения неопределенных
II. Методы решений уравнений в целых числах.
1. О Диофанте и диофантовых уравнениях.
2. Уравнения первой степени с двумя неизвестными в общем виде: 6-7
а) алгоритм Евклида (метод остатков);
б) метод рассеивания;
в) решение задач на деление с остатком.
3. Решение неопределенных уравнений степени выше первой:
а) решение уравнений с двумя переменными как
квадратных, относительно одной из переменных;
б) решение уравнений методом разложения на множители;
в) метод бесконечного спуска
4. Пифагоровы тройки.
5. Великая теорема Ферма.
Развивающая функция обучения не просто требует от учителя изложения знаний в определенной систем, а предполагает также учить учащихся мыслить, искать и находить ответы на поставленные вопросы. добывать новые знания. опираясь на уже известные. Уместно в связи с этим привести слова французского ученого М. Монтеня: « Мозг, хорошо устроенный, стоит больше, чем мозг хорошо наполненный».
Известно, что на развитие познавательной активности и творческого мышления решающее значение оказывает рассмотрение различных способов решения задач, ознакомление с различными методами, существующими в математических исследованиях, и закрепления их в практической деятельности.
Известный математик-педагог Д. Пойа в книге «Как решать задачу» писал: «Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысл, оригинальности, изобретательности».
Обучение должно в разумной мере проходить в форме повторного открытия, а не простой передачей суммы знаний. Надо изучать учебную дисциплину не столько ради лишних фактов, сколько ради процесса их получения, и тогда, по словам Б. Рассела, предмет предстанет как могучее орудие познания.
Обучение в школе должно руководствоваться формулой: « Овладение = Усвоение +Применение знаний на практике». Эффективным средством обучения и развития является организация учебных исследований, цель которых состоит в том, чтобы помочь учащимся самостоятельно открыть новые знания и способы деятельности, углубить и систематизировать изученное.
Тема «Решение уравнений в натуральных и целых числах» недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и в заданиях на экзаменах. В данной работе выделены основные методы решений уравнений в натуральных и целых числах и приводится система тренировочных упражнений для закрепления каждого из рассмотренных методов. При решении уравнений в натуральных и целых числах степени выше первой можно условно выделить следующие методы решения:
1. Метод рассеивания.
2. Метод остатков.
3. Метод разложения на множители.
4. Решение уравнений с двумя переменными, как квадратных относительно одной из переменных.
5. Метод бесконечного спуска.
ІІ. Методы решений уравнений в целых числах.
1. О Диофанте и диофантовых уравнениях.
Одним из самых своеобразных древнегреческих математиков был Диофант Александрийский, труды которого имели большое значение для алгебры и теории чисел. До сих пор не выяснены ни год рождения, ни дата смерти Диофанта; полагают, что он жил в 3 в. н. э. В одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраической загадки, представляющей надгробную надпись на его могиле:
Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил,
Отнят он был у отца могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Задача-загадка сводится к составлению и решению уравнения:
Откуда х=84 — вот сколько лет жил Диофант.
Из работ Диофанта самой важной является «Арифметика», из 13 книг которой только 6 сохранились до наших дней. Эти книги были открыты в Венеции в 1463г. Региомонтаном, который в связи с этим писал, что в произведении Диофанта сосредоточен « весь цвет арифметики, искусство неизвестной».
«Арифметика» посвящена некоему Дионисию, обращаясь к которому, Диофант пишет: «Зная, достопочтеннейший Дионисий, что Вы очень усердно изучаете задачи, касающиеся чисел, я взялся изложить природу их и могущество, начиная с самых основ, на которых все это покоится. Это, может быть, покажется более трудным, чем есть на самом деле потому, что еще неизвестно. Начинающие склонны скоро терять мужество. Но Вы легко разберетесь в этом благодаря устремлению Вашего ума и моим пояснениям».
В сохранившихся книгах Диофанта содержится 189 задач с решениями. В первой изложены задачи, приводящиеся к определенным уравнениям первой и второй степени. Остальные же пять книг содержат в основном неопределенные уравнения. В этих уравнениях еще нет систематической теории неопределенных уравнений, методы решения меняются от случая к случаю. Диофант довольствуется каким-нибудь одним решением, целым или дробным, лишь бы оно было положительным.
В школьных учебниках, да и в других книгах по математике, большинство рассуждений и доказательств проводится не на конкретных примерах, a в общем виде. И может возникнуть впечатление, что и сами математические открытия делаются обычно в общем виде. А в действительности дело обстоит далеко не так. До того как изложить общий способ решения задачи или доказательства теоремы, математик очень часто — почти всегда – ищет частные примеры, подтверждающие или опровергающие его мысль. Если пример приведет к опровержению мысли – поиск продолжают в новом направлении, а если пример подтвердит ее – ищут общее доказательство.
Вот и мы сначала попробуем решить частный пример.
На складе имеются гвозди в ящиках по 16, 17 и 40 кг. Может ли кладовщик выдать 100 кг гвоздей, не вскрывая ящики?
Попробуем решить задачу, составив уравнение обычным путем.
Итак, допустим, что задача решена: ящиков по 16 кг будет x штук; по 17 кг – y штук, по 40 кг – z штук. Всего выдано 100 кг, отсюда уравнение:
16x+17y+40z=100, и что делать с этим уравнением – совершенно не понятно.
Но можно рассуждать и так. Ящиков по 40 кг не может быть больше двух. Ибо 40*3=120, это больше чем надо. И два тоже не может быть, т. к. 40*2=80, 100-80=20, а 20 кг можно набрать, только вскрыв хотя бы один ящик.
Может быть, взять один ящик по 40 кг, а оставшиеся 60 кг набрать, комбинируя ящики по 16 и 17 кг: если взять один ящик по 17 кг, то останется 43 кг и набрать их ящиками по 16 кг невозможно; если взять два ящика по 17 кг, то 60-17*2=26 и целых ящиков по 16кг не получится ; если же взять три ящика по 17 кг, то останется 9 кг, которые придется выдавать, вскрыв какой — нибудь ящик. Получается, что ящики по 40 кг нам вовсе не нужны. Если задача имеет решение, то комбинировать придется ящики только по 16 и17 кг. Значит, получается уравнение:
100 не делится ни на 16, ни на 17, и, значит, надо посмотреть, что будет, если из 100 вычитать 17, 17*2, 17*3, 17*4, 17*5. Если разность будет делиться на 16, то задача имеет решение, если нет, то кладовщику придется вскрывать хотя бы один ящик. 83 на 16 не делится, 66 – не делится, 49 – не делится, но 32=16*2, и задача решена: 17*4+16*2=100, т. е. надо выдать четыре ящика по 17 кг и два ящика по 16кг. Это решение единственное, т. е. других вариантов нет.
Можно было бы, увидев, что ящики по 40 кг для решения задачи не нужны, пойти дальше другим путем. Если взять 6 ящиков по 16 кг, т. е. подобрать такое число, делящееся на 16, которое ближе всего к 100 , то окажется, что до 100 не хватает 4 кг, значит, четыре ящика из этих шести надо заменить четырьмя ящиками по 17 кг, и получим тот же результат.
Задач, похожих на эту, очень много, и многие из них имеют практическое значение. Соответствующие уравнения могут иметь неизвестные не только в первой степени, во второй, любой другой. Да и вопросы, вытекающие из дополнительных условий, могут оказаться самыми разнообразными. И опять приходим к новому разделу математики. Этому разделу положил начало Диофант.
Раздел математики называют «диофантовым анализом», в свою очередь диофантовый анализ является частью исключительно интересного раздела современной математики – теории чисел. В теории чисел созданы специальные методы решения диофантовых ( их еще называют неопределенными ) уравнений.
2. Уравнение первой степени с двумя неизвестными.
Рассмотрим уравнение первой степени с двумя неизвестными
где a и b – целые числа, отличные от нуля, а с – произвольное целое. Будем считать, что коэффициенты a и b не имеют общих делителей, кроме единицы. Действительно, если общий наибольший делитель этих коэффициентов d=(a, b) отличен от единицы, то справедливы равенства a=a1d, b=b1d; уравнение (1) принимает вид
и может иметь целые решения только в том случае, когда c делится на d. Таким образом, в случае (a, b)=d все коэффициенты должны делиться нацело на d, и, сокращая на d, придем к уравнению
a1 x+b1 y+c1=0 (c1 =
коэффициенты которого a 1и b 1 взаимно просты.
Рассмотрим сначала случай, когда c=0. Уравнение (1) перепишется так:
Решая это уравнение относительно x, получим
x= —
Обозначим 




Мы получаем формулы, содержащие все целые решения уравнения (1*)
x=-bt, y=at (t=0, 

Перейдем теперь к случаю, когда c
Покажем прежде всего, что для нахождения всех целых решений уравнения (1) достаточно найти какое – нибудь одно его решение, т. е. найти такие целые числаx 0,y 0 , для которых
Теорема I.Пусть a и b взаимно простые и 


Пусть 

Так как y-y 0 – целое число и числа a и b взаимно просты, то x-x0 должно нацело делиться на b, т. е. x-x 0 имеет вид x-x 0=- bt, где t – целое. Но тогда
y-y 0=
x=x 0-bt, y=y 0+at. (2)
Таким образом доказано, что всякое решение 

Но так как 

Итак, если известно одно решение уравнения ax +by +c=0, то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид
x=x 0-bt, y=y 0+at (t=0, 

Заметим, что в случае, когда с=0, найденные раньше формулы решений x=-bt, y=at (t=0, 

могут быть получены из только что выведенных формул x=x 0-bt, y=y 0+at (t=0, 


а) Алгоритм Евклида.
Пусть дано уравнение:127x-52y+1=0.
Преобразуем отношение коэффициентов при неизвестных.
Прежде всего, выделим целую часть неправильной дроби 


Правильную дробь 



Проделаем такие же преобразования с полученной в знаменателе неправильной дробью 



Теперь исходная дробь примет вид: 

Повторим те же рассуждения для дроби 



Тогда: 

Выделяя целую часть неправильной дроби 




Мы получим выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби – одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби 
2+ 






Приведем полученное выражение к общему знаменателю и отбросим его, тогда
Из сопоставления полученного равенства с уравнением 127x-52y+1=0 следует, что x=9, y=22 будет решением этого уравнения и, согласно теореме, все его решения будут содержаться в прогрессиях x=9+52t, y=22+127t, (t=0, 

Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения ax +by +c=0 надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше.
Приведенный метод носит название метода последовательного деления с остатком или алгоритма Евклида, поскольку он впервые был изложен в его « Началах».
Отметим преимущество и недостаток цепных дробей по сравнению, например, с десятичными. Удобство заключается в том, что их свойства не связаны ни с какой системой счисления. По этой причине цепные дроби эффективно используются в теоретических исследованиях. Но широкого практического применения они не получили, т. к. для них нет удобных правил выполнения арифметических действий, которые имеются для десятичных дробей.
б ) Метод рассеивания
В Индии, где (как и в Китае) неопределенные уравнения решались в связи с астрологическими запросами и расчетами, ставился вопрос о нахождении именно целочисленных решений неопределенных уравнений. Намеки на общее решение диофантовых уравнений первой степени, т. е. вида, встречаются в трудах индийского астронома Ариабхатты, подробное же решение предложили индийские математики Брахмагупта и Бхаскара. Общий метод для решения в целых числах неопределенных (диофантовых) уравнений первой степени с целыми коэффициентами был назван в Индии методом рассеивания (в смысле размельчения) .
Воспользуемся этим методом для решения следующей задачи:
«Найти два целых числа, зная, что разность произведений первого на 19 и второго на 8 равна 13».
В задаче требуется найти все целые решения уравнения
Выражая y — неизвестное с наименьшим по абсолютной величине коэффициентом через x, получим:
y= 
Нам нужно теперь узнать, при каких целых значениях x дроби, составляющие значение y являются тоже целыми числами. Перепишем уравнение(2) следующим образом:
y= 2x+ 
Из уравнения (3) следует, что y при x целом принимает целое значение только в том случае, если выражение 

вопрос сводим к решению в целых числах уравнения (4) с двумя неизвестными x и y 1; его можно записать так:
Это уравнение имеет по сравнению с первоначальным (1) то преимущество, что 3 – наименьшая из абсолютных величин коэффициентов при неизвестных – меньше, чем в (1), т. е. 8. Это было достигнуто благодаря тому, что коэффициент при x (19) был заменен остатком от деления на 8.
Продолжая тем же способом, мы получим из (5) :
x= 

Итак, неизвестное x при целом y1 только тогда принимает целые значения 

3y2-2y1=13 (8) Далее,
y1= 


Это самое простое из всех рассмотренных неопределенных уравнений, т. к. один из коэффициентов равен 1.
Из (11) получаем: y2=2y3+13 (12)
Отсюда видно, что y2 принимает целые значения при любых целых значениях y3. Из равенств (6), (9), (12), (3) путем последовательных подстановок можно найти следующие выражения для неизвестных и уравнения (1):
Таким образом, формулы
при y3= 0, 

В следующей таблице приведены примеры таких решений.
Этот прием почти полностью совпадает с методом индийцев и был назван ими методом рассеивания (размельчения) именно потому, что неопределенное уравнение сводится к цепи уравнений со все уменьшающимися по абсолютной величине коэффициентами. К решению неопределенного уравнения первой степени сводятся иногда задачи, связанные с практикой и повседневной жизнью человека.
Вот один пример.
«Некто покупает в магазине вещь стоимостью в 19 р. У него имеются лишь 15 трехрублевок, у кассира же – лишь 20 пятирублевок. Можно ли расплатиться и как?»
Задача сводится к решению в целых положительных числах диофантова уравнения:
где x

x=

y=

Ввиду того, что x и y должны быть положительными и, учитывая условие задачи, легко установить, что
0

т. е. y2 может принимать только два значения: 0 и1. Отсюда вытекает только два возможных решения:
А вот еще одна задача.
«Можно ли отвесить 28 г некоторого вещества на чашечных весах, имея только четыре гири весом в 3 г и семь гирь весом в 5 г?»
Решим диофантово уравнение:
x=


Из условий задачи вытекает, что



Однако, y1=0 и y1=1 противоречат условию задачи x
При ревизии торговых книг кооператива одна из записей оказалась залитой чернилами и имела такой вид:
Невозможно было разобрать число проданных метров, но несомненно, что число это не дробное; в вырученной сумме можно было различить только последние три цифры, да установить еще, что перед ними были три какие – то другие цифры.
Может ли ревизионная комиссия по этим следам установить запись?
Обозначим число метров через x. Вырученная сумма выразится в копейках через 4936x.
Число, выражаемое тремя залитыми цифрами в записи денежной суммы, обозначим через y. Это, очевидно, число тысяч копеек, а вся сумма в копейках изобразится так:
или, после сокращения на 8,
В этом уравнении x и y – числа целые и притом y не больше 999, т. к. более чем из трех цифр оно состоять не может. Решаем уравнение, как раньше было указано:
y=5x-1+

(Здесь мы приняли 

Есть целое число, а т. к. 2 не делится на 125, то
должно быть целым числом, которое мы и обозначили через t ). Далее из уравнения

x=4-31t+
t1=
100

100



Очевидно, для t 1 существует только одно целое значение:t1=1,
и тогда x=98, y=483 т. е. было отпущено 98 метров на сумму 4837 р. 28 к. Запись восстановлена.
Покупка почтовых марок.
Требуется на 5 рублей купить 20 штук почтовых марок – 40-копеечных, 25-копеечных и 5-копеечных. Сколько окажется марок каждого достоинства?
В этом случае у нас имеется два уравнения с тремя неизвестными:

где x –число марок 40-копеечных, y — 25-копеечных, z — 5-копеечных. Вычитая из первого уравнения, деленного на5, второе, получим одно уравнение с двумя неизвестными:
y=20-
Очевидно, 
Подставляем выражения для x и y во второе из исходных уравнений:
Т. к. x 


0
откуда заключаем, что для t возможны только два целых значения: t=1 и t=2.
Соответствующие значения x, y и z таковы:
Итак, покупка марок может быть произведена только двумя способами.
На 50 рублей куплено 100 штук разных фруктов. Цены на фрукты таковы: арбуз, штука – 5 руб. ; яблоки, штука – 1 руб.; сливы, штука – 10 коп. Сколько фруктов каждого вида было куплено?
Обозначим число арбузов через x, яблок через y и слив через z, составим два уравнения:



Дальнейший ход решения:
y=

t=
Из неравенств 1-9t
устанавливаем, что- 
Подставив эти значения x и y во второе уравнение, получаем: z=60.
Итак, куплены были 1 арбуз,39 яблок, 60 слив.
Отгадать день рождения.
Умение решать неопределенные уравнения дает возможность выполнить следующий математический фокус.
Вы предлагаете товарищу умножить число даты его рождения на 12, а номер месяца – на 31. Он сообщает вам сумму обоих произведений, и вы вычисляете по ней дату рождения.
Если, например, товарищ ваш родился 9 февраля, то он выполняет следующие выкладки:
9*12=108, 2*31=62, 108+62=170.
Это последнее число, 170, он сообщает вам, и вы определяете задуманную дату. Как?
Задача сводится к решению неопределенного уравнения 12x+31y=170 в целых положительных числах, причем число x месяца не больше 31 , а номер месяца y не больше 12.
x=


y=



y=2(1-5 t1)- 2t1=2-12 t1,
x= 14-3(2-12 t1)+1-5 t1=9+31 t1.
0 

—
Дата рождения 9-е число второго месяца, т. е. 9 февраля.
Проанализируем решение данных задач.
1) Основное уравнение заменялось рядом неопределенных уравнений, у которых все три коэффициента становились не больше (по модулю), чем у предыдущего.
2) Уравнение имело целые, а потом и натуральные решения;
3) Т. к. в последнем уравнении коэффициент при одной из переменных оказался равным 1 значит, что данное уравнение разрешимо в целых числах (очевидно, что уравнения ax+y=c и x+by=c всегда имеют целые решения);
4) В формулах общего диофантового уравнения содержалось частное решение.
Мы овладели практикой нахождения целочисленных решений линейного уравнения с двумя неизвестными, руководствуясь следующим алгоритмом:
а) данное уравнение разрешают относительно переменной с наибольшим коэффициентом ( по модулю);
б) в полученном уравнении выделяют целую часть, а дробную часть обозначают за новую переменную, в результате получается новое неопределенное уравнение;
в) последнее уравнение решают, руководствуясь пунктами а) и б) до тех пор, пока один из коэффициентов не будет равен 1;
г) поочередно выражаем все переменные через последнюю неизвестную, пока не сформируем ответ.
в) Решение задач на деление с остатком.
Задача 1. При делении двузначного числа на 6 в остатке получилось число, равное цифре его десятков, а при делении того же числа на 10 частное было равно 3, а остаток цифре единиц делимого. Найдите все такие двузначные числа.
Обозначим искомое число через 
Из второго уравнения получаем:
Преобразуем первое уравнение:
Отсюда цифра y нечетна и делится на 3 т. е. y=3 или y=9 .
Если числа 826 и 4373 разделить на одно и то же натуральное число, то получатся соответственно остатки 7 и 8 . Найдите все значения делителя.
Решение: Запишем соответствующие равенства:
где b – неизвестный делитель, q1 и q2 – неполные частные.
Разложим числа 819 и 4365 на простые множители:
Следовательно, общими делителями чисел 819 и 4365 являются числа 1, 3 и 9. Но общие делители, равные 1 и 3, невозможны, т. к. остаток должен быть меньше делителя. Остается число 9.
При делении натурального числа а на 2 в остатке получается 1, а при делении на 3 – остаток 2. Какой остаток получится при делении а на 6?
где остаток r удовлетворяет неравенству 0
Случай r=0 невозможен, иначе число a делится на 2 и на 3.
Случай r=1 – тоже, т. к. тогда a при делении на 3 дает в остатке 1 , а не 2.
По аналогичным причинам отпадают случаи r=2, r=3, r=4.
Случай r=5 возможен, например, при a=5 или a=11.
Докажите, что два натуральных числа при делении на их разность дают одинаковые остатки.
Обозначим эти числа через a и b, где a 
Тогда a=(a-b)q1+r1, b=(a-b)q2+r2.
Вычтем почленно эти равенства:
a-b=(a-b)( q1- q2)+( r1- r2).
Отсюда разность r1- r2 делится на a-b.
Но r1 

3. Решение неопределенных уравнений степени выше первой.
а) Решение уравнений с двумя переменными как квадратных относительно одной из переменных.
Задача 1.Решите в целых числах
Если попытаться решить данное уравнение методом разложения на множители, то это достаточно трудоемкая работа, поэтому это уравнение можно решить другим методом. Рассмотрим уравнение как квадратное относительно x
x1,2=

Данное уравнение имеет решение тогда и только тогда, когда дискриминант этого уравнения равен нулю, т. е. -9(y+1)2=0, отсюда y=-1. Если y=-1,то x=1.
Задача 2. Решите в целых числах уравнение
Решение: 1) Очевидно, x=0, y=0 – решение уравнения. Перепишем уравнение в виде
1-й случай. Если y2-1=0 , то y=1, y=-1.
При y=1имеем x+1=0, x=-1, x
При y=-1 имеем –x+1=0, x=1, x 
2-й случай. Если y2-1
y 
Уравнение (*) является квадратным относительно переменной x, тогда
x1,2=

Так как y

Найдем целые значения переменной y, удовлетворяющие уравнению
(1) 



y= 
Значит, данное уравнение имеет три пары решений: (0;0), (-1;1), (1;1).
Задача 3. Решите уравнение 5×2-2xy+2y2-2y+1=0.
Решение: Рассмотрим данное уравнение как квадратное относительно x с коэффициентами, зависящими от y,
Найдем четверть дискриминанта



Отсюда следует, что уравнение имеет решение только тогда, когда
— 


Ответ:
б) Метод разложения на множители.
Задача 1. Решите уравнение в целых числах:
Решение: Разложим левую часть данного уравнения на множители:
(x-y)(x+y)=91. Так как 91=1*91=91*1=7*13=13*7=-1*(-91)=-91*(-1)= =-7*(-13)=-13*(-7), то решение данного уравнения сводится к решению восьми систем:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
Ответ: (46; 45), (46; -45), (-46; -45), (-46; 45), (10; 3), (10; -3), (-10; -3), (-10; 3).
Задача 2.Решите в целых числах x3+91=y3.
Перепишем данное уравнение в следующем виде: y3- x3=91, разложим левую часть на множители: (y-x)(y2+xy+x2)=91. Заметим, что y2+xy+x2=(y+



1)
решая данную систему, получаем (5; 6), (-6; -5) ;
2)
система не имеет решений в целых числах;
3)
решения в целых числах нет;
4)
решая данную систему, получаем (-3 

Ответ: (5; 6), (-6; -5), (-3 

Задача 3. Решите в целых числах xy = x+y.
Перепишем данное уравнение в следующем виде:
Левую часть данного уравнения разложим на множители, применяя способ группировки:
x(y-1)-(y-1)=1




Ответ: (2 

в) Метод «бесконечного спуска».
Для доказательства многочисленных теорем, которые Ферма сформулировал в теории чисел, он ввел метод бесконечного спуска. В чем же заключается этот метод? К примеру, надо доказать, что какое – то уравнение не имеет натуральных решений. И пусть из предположения, что у данного уравнения все же есть решение в натуральных числах, можно вывести, что у него есть еще меньшее, тоже натуральное решение. Тогда из существования этого меньшего решения делается вывод о существовании еще меньшего решения и т. д. Но так как натуральные числа не могут неограниченно уменьшаться, то сделанное предположение неверно и решения данного уравнения в натуральных числах не существует.
Решение уравнений методом бесконечного спуска проходит по следующей схеме: предположив, что уравнение имеет решения, мы строим некоторый бесконечный процесс, в то время как по самому смыслу задачи этот процесс должен чем – то кончаться.
Часто метод бесконечного спуска принимается в более простой форме. Предположив, что мы уже добрались до естественного конца, видим, что «остановиться» не можем.
Историческая справка. Метод бесконечного спуска изобрели, по — видимому, древнегреческие математики. Есть основания полагать, что Ферма пытался доказать свою великую теорему именно этим методом.
Применим метод бесконечного спуска к решению уравнения.
Задача. Решить в целых числах уравнение 4×3-2y3-z3=0.
Решение: Здесь левая часть уравнения не разлагается на целые множители и вообще не поддается преобразованиям.
Запишем данное уравнение в виде
Следовательно, z3 — четное, значит должно делиться на два, т. е. z=2z1 , z1
Из уравнения (*) видно, что y четное, т. е. y=2y1, y1 
Из уравнения (**) следует, что x четное, т. е. x=2×1, x1
Получаем уравнение вида (1).
Из всех проделанных рассуждений можно сделать следующие выводы. В – первых, числа x, y, z должны быть четными. Во – вторых, числа x1, y1, z1 , т. е. 

Итак, оказалось, что числа, удовлетворяющие уравнению (1), четные, и сколько раз мы не делили бы их на 2, получаем числа, которые так же делятся на 2. Единственное число, обладающее этим свойством — есть нуль.
Следовательно, данное уравнение имеет единственное решение x=0, y=0, z=0.
Решите в целых числах уравнение x3-3y3-9z3=0. (*)
Решение: Видно, что левая часть уравнения (*) не поддается никаким преобразованиям. Поэтому, исследуя характер целых чисел, получим:
Число x3 кратно 3, значит и число x кратно 3, т. е.
Тогда y3 кратно 3, а значит и y кратно 3, т. е.
Из этого уравнения следует, что z3 кратно 3, а значит и z кратно 3, т. е. z=3z1.
Из всех проделанных рассуждений можно сделать вывод, что
1) числа x, y, z кратны 3;
2) числа x1, y1, z1 , т. е. 
Итак, оказалось, что числа, удовлетворяющие уравнению (*), кратны 3, и, сколько раз мы не делили бы их на 3, получаем числа кратные 3. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0).
4. Пифагоровы тройки.
Мы знаем, что общие теории никогда не возникают на пустом месте. Сначала появляются отдельные задачи, а уж потом находятся люди, понимающие, что наступило время перехода от таких задач к общим приемам и методам.
Вот, например, еще одна частная задача на неопределенные уравнения – теперь уже второй степени, возникшая примерно за две тысячи лет до Диофанта в Древнем Египте (известно, что Диофант хорошо ее знал и часто использовал):
Если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник – прямоугольный.
Этот факт использовали для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид это надо было уметь. Поступали довольно просто. На веревке на равном расстоянии друг от друга завязывали узлы. В точке С, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали второй колышек в точке В (СВ=4) и натягивали веревку так, чтобы АС=3 и АВ=5.
Треугольник с такими длинами сторон называют египетским.
Безошибочность такого построения следует из теоремы, обратной теореме Пифагора: если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
И действительно, числа 3, 4 и 5 – корни уравнения x2+y2=z2.
Возникает вопрос: нет ли у этого уравнения других целочисленных решений?
Нетрудно догадаться, что числа 5, 12, 13 тоже можно считать корнями этого уравнения. А есть ли еще такие тройки чисел? Нельзя ли, взяв произвольно одно из чисел, указать остальные два? Такие вопросы интересовали еще мудрецов Древнего Вавилона. Они нашли ответы на них. Знал это и Пифагор.
Один из путей решения уравнения x2+y2=z2 в целых числах оказался довольно простым. Запишем подряд квадраты натуральных чисел ( «квадратные числа», как говорили древние), отделив их друг от друга запятой. Под каждой запятой запишем разность между последовательными квадратами:
В нижней строке также есть квадратные числа. Первое из них 9=32, над ним 16= 42 и 25= 52, знакомая нам тройка 3, 4, 5. Следующее квадратное число в нижней строке 25, ему соответствуют 144 и 169, отсюда находим вторую известную нам тройку 5, 12, 13.Если продолжить строку квадратных чисел и подсчитать соответствующие разности, то во второй строке найдем 49= 72, этому числу отвечают в строке квадратов 576= 242 и 625= 252. Это уже третья тройка. Она была известна еще в Древнем Египте.
Теперь мы имеем право сформулировать такую теорему:
Каждое нечетное число есть разность двух последовательных квадратов.
Составлять такие строки – довольно трудоемкое занятие. По формулам находить такие тройки чисел и проще и быстрее. Эти формулы – правила были известны уже две с половиной тысячи лет назад.
Проверим, что, если χ – нечетное число, то y = 

Проверим также, что в этом случае равенство x2+y2=z2 выполняется, т. е. числа, найденные по такому правилу, всегда будут составлять решение интересующего нас неопределенного уравнения. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровыми тройками». По этому правилу можно получить уже известные нам тройки:
если x=3 , то y=

если x=5 , то y= 

если x=7, то y= 
Других мы пока не знаем, но следующее за 7 нечетное число 9, тогда y=40 и z=41. Проверим наши вычисления:
Следующим шагом было установление правила вычисления всех, а не только некоторых пифагоровых троек.
Перепишем уравнение Пифагора следующим образом:
Это означает, что число x должно разлагаться на два неравных множителя z+y и z-y, которые мы обозначим так, что получится такая система:
(при этом надо иметь в виду, что a
Длины сторон (целочисленные) прямоугольных треугольников
Ясно, что таблицу можно расширить и вправо, и вниз. Подчеркнем главное – уравнение решено, мы знаем способ вычисления всех возможных целочисленных значений длин сторон прямоугольных треугольников.
5.Великая теорема Ферма.
Перейдем теперь к одной из самых знаменитых задач диофантова анализа, получившей название Великой теоремы Ферма. Начнем с истории возникновения этой теоремы.
Пьер Ферма (1601 – 1665), выдающийся французский математик, был одним из ученых, которые в XVII в. развили метод координат и заложили основы высшей математики. Он является одним из создателей теории чисел, т. е. той ветви математики, в которой изучаются свойства целых чисел.
Для исследований Ферма исходным пунктом нередко служила математика древних, в частности «Арифметика» Диофанта, изданная в 1621 г. Баше де Мезириаком. На одной из страниц второй книги своего произведения Диофант решает следующую задачу: «Найти два квадрата, сумма которых тоже является квадратом».
На полях вышеуказанной страницы экземпляра «Арифметики» Диофанта, которым пользовался Ферма, имеется собственноручная заметка последнего: «Наоборот, невозможно разложить куб (т. е. z3) на два куба или биквадрат (т. е. z4) на два биквадрата и, вообще, никакую степень, выше второй, нельзя разложить на сумму двух степеней с тем же показателем. Я нашел поистине удивительное доказательство этого предложения, но поля книги слишком узки, чтобы его изложить».
Итак, речь идет о следующем: доказать, что уравнение
не имеет целых решений для n 
Это предложение и было названо «Великой, или большой теоремой Ферма» или «Последней теоремой Ферма». Сам Ферма знал о ее связи с задачей о площади целочисленного прямоугольного треугольника. Одно из его замечаний к Диофантовой «Арифметике» гласит: «Площадь прямоугольного треугольника в числах не может быть квадратом (целого числа)». Ферма показал затем, что это утверждение эквивалентно великой теореме для n=4, и доказал его.
Его доказательство – единственное полное теоретическо – числовое доказательство Ферма, которое дошло до наших дней. Здесь он применил новый метод – метод бесконечного спуска.
Начиная с XVIII в. были сделаны большие усилия для доказательства теоремы Ферма. Эйлер ее доказал для n=3 и n=4. Для n=5 доказательство было сделано в 20-х годах XIX в. Лежандром и Дирихле. В 1847 г. Французский математик Г. Ламэ дал доказательство для n=7.
Известный успех был достигнут в рассматриваемой задаче немецким математиком Е. Куммером, наметившим общий подход к проблеме, с помощью которого он нашел доказательства для всех простых чисел, содержащихся между 3 и 100. Широкая известность « Большой теоремы Ферма» и нездоровый ажиотаж к поискам ее доказательства возникли в 1907 г., когда за ее решение была объявлена премия в 100000 немецких марок. Эта премия из – за ряда инфляций в Германии была в последствии аннулирована.
В 1960 г. Посредством вычислений, выполненных на ЭВМ, было найдено, что эта теорема верна для всех n

Конец XX в. ознаменовался для математиков настоящей сенсацией: попытки доказать великую теорему Ферма наконец – то увенчались успехом!
В 1995 г. В одном из ведущих математических журналов – «Анналы математики» — было опубликовано полное доказательство теоремы. Разбитое на две статьи, оно заняло весь номер – в общей сложности более 100 страниц. Основная часть доказательства принадлежала английскому математику Э. Уайлсу, профессору Принстонского университета. На последнем этапе к работе подключился Р. Тейлор, профессор Оксфордского университета.
Идеи Уайлса опирались на замечательную связь между уравнением Ферма x n+yn= zn и эллиптическими кривыми, задаваемыми уравнением y2=x(x-an)(x-cn).
Так завершилась 350–летняя история доказательства великой теоремы.
Великая теорема Ферма носит как будто бы частный характер. Но попытки ее доказательства обогатили математику новыми идеями, методами, теориями. В этом и состоит непреходящее значение великой теоремы.
Современной постановкой диофантовых задач мы обязаны Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределенных уравнений только в целых числах. Но это не было изобретением Ферма – он только возродил интерес к поиску целочисленных решений. А, вообще, задачи, допускающие только целые решения, были распространены во многих странах в очень далекие от нас времена. Древние математики находили в большинстве случаях одно, реже несколько решений неопределенных задач и в основном подбором. Правда за этим подбором, как правило, стояла система, разгадав которую, можно записать все искомые решения уравнения.
Решение неопределенных уравнений – очень увлекательная задача. Рассмотрение теории диофантовых уравнений необходимо и весьма полезно для формирования математической культуры. Процесс решения диофантовых уравнений позволяет проводить содержательные исследования на базе относительно элементарных средств; развивать логическое мышление, прививать навыки самостоятельной работы, решать задачи практической направленности и др.
Я считаю, что материал, представленный в работе, может использоваться как учащимися, интересующимися математикой, для самостоятельного изучения, так и в работе математических кружков и при проведении элективных занятий.
Для работы на занятиях можно предложить, например, задачи из учебника начала прошлого века А. Малинина и К. Буренина (несколько задач приводится в приложении). Также в приложении дается конспект урока в 7 классе «Уравнения первой степени с двумя неизвестными.» Автор учебника: , , . Алгебра. 7 класс: учеб. для общеобразоват. учреждений. М.: Просвещение, 2012.
Избранные задачи на диофантовы уравнения из «Руководства алгебры» для гимназий, реальных училищ и учительских институтов (составители А. Малинин и К. Буренин. Москва. 1913)1.
Решите в целых числах уравнения:
Решите в целых положительных числах системы уравнений:
Метод неопределенных коэффициентов и его универсальность
Разделы: Математика
Применение метода неопределённых коэффициентов основано на следующих двух теоремах.
Теорема №1 (о многочлене, тождественно равном нулю).
Если при произвольных значениях аргумента x значение многочлена f(x) = а0+ а1х + а2х 2 +. + а nx n , заданного в стандартном виде, равно нулю, то все его коэффициенты а0, а1, а2, . аn равны нулю.
Теорема №2 (следствие теоремы № 1).
Деление многочлена на многочлен.
Пример 1. Выполнить деление многочлена х 5 – 6х 3 + 2х 2 -4 на многочлен х 2 – х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что х 5 – 6х 3 + 2х 2 -4 = (х 2 – х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 2 – х + 1). Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 5 – 2 = 3.
Многочлены Q(x) и R(x) имеют вид:
Раскроем скобки в правой части равенства:
Для отыскания неизвестных коэффициентов получаем систему уравнений:
Ответ: Q(x) = x 3 + x 2 — 6x — 5, R(x) = x + 1.
Пример 2. Выполнить деление многочлена х 7 –1 на многочлен х 3 + х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что х 7 –1 = (х 3 + х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 3 + х + 1).
Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 7– 3 = 4.
Многочлены Q(x) и R(x) имеют вид: Q(x) = q 4x 4 + q 3x 3 + q 2x 2 + q 1x + q0,
R(x) = r 2x 2 + r 1x + r0.
Подставим Q(x) и R(x):
Раскроем скобки в правой части равенства:
Получаем систему уравнений:
Ответ: Q(x) = x 4 — x 2 — x + 1, R(x) = 2x 2 — 2.
Расположение многочлена по степеням.
Возьмем функцию 
Задача сводится к нахождению неизвестных коэффициентов а0, а1, . аn. В каждом конкретном случае эти числа найти легко. Действительно, расположим многочлены, находящиеся в левой и правой частях равенства, по степеням x. Так как мы имеем тождество, то (по теореме № 2) коэффициенты при одинаковых степенях x должны быть равны между собой. Приравняв коэффициенты правой части соответствующим заданным коэффициентам левой, мы придем к системе n+1 уравнений с n+1 неизвестными а0, а1, . аn , которую нужно решить.
Пример 3. Расположим многочлен 

Приравниваем коэффициенты при одинаковых степенях и получаем систему:
Решая систему, находим:
Ответ: 
Пример 4. Расположим f(x) = х 4 — 8х 3 + 24х 2 — 50х + 90 по степеням (х-2).
Решение: Полагаем х4 — 8х 3 + 24х 2 — 50х + 90
Ответ: f(x) =
Представление произведения в виде многочлена стандартного вида.
Пример 5. Не выполняя действий, представим в виде многочлена стандартного вида произведение (х — 1)(х + 3)(х + 5).
Решение: Произведение есть многочлен третьей степени, коэффициент при старшем члене равен 1, а свободный член равен (- 15), тогда запишем:
(х — 1)(х + 3)(х + 5) = х 3 + ах 2 + вх — 15, где а и в — неизвестные коэффициенты.
Для вычисления их положим х = 1 и х = — 3, тогда получим:

Ответ: х 3 +7х 2 + 7х — 15.
Разложение многочлена на множители
Пример 6. Дан многочлен
Разложим его на множители, если известно, сто все его корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 30. Следовательно, их следует искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -2, -5, 1 и 3. Следовательно х 4 + 3х 3 — 15х 2 — 19х + 30 = (х — 1)(х — 3)(х + 2)(х + 5)
Пример 7. Дан многочлен 
Разложим его на множители, если известно, сто все его корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 84. Следовательно, их следует искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -7,-2,2,3. Следовательно х 4 + 4х 3 — 25х 2 — 16х + 84 = (х — 2)(х — 3)(х + 2)(х + 7)
Пример 8. Разность 
Решение: Так как,
Тогда
Положим 
Тогда
Решая данную систему уравнений, получим а = 5, b = -4.
Значит 
Аналогично устанавливаем, что
Следовательно
Пример 9. Является ли разность 
Решение: Т.к.
тогда —
Положим 
Тогда 
из второго уравнения 
b 2 = 12,5 — — не удовлетворяет условию задачи, или b 2 = 9, откуда b = -3 или b = 3 — не удовлетворяет числу 
Аналогично,
Окончательно получаем: 
Уничтожение иррациональности в знаменателе
Пример 10. Избавимся от иррациональности в знаменателе:
Решение:
отсюда
Раскроем скобки, сгруппируем:
Ответ:
Пример 11. Избавимся от иррациональности в знаменателе:
Решение: 
отсюда
Раскроем скобки, сгруппируем
Отсюда
Итак
Следовательно
Ответ:
Применение метода неопределенных коэффициентов при решении уравнений
Пример 12. Решим уравнение х 4 + х 3 — 4х 2 — 9х — 3 = 0.
Решение: Предположим, что корни уравнения — целые числа, тогда их надо искать среди чисел
Если х = 1, то 
если х = -1, то 
если х = 3, то 
если х = -3, то
Отсюда делаем вывод, что рациональных корней наше уравнение не имеет.
Попробуем разложить многочлен 

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:
Так как bd = -3, то будем искать решения среди вариантов:
Проверим вариант № 2, когда b = —1; d = 3:
Пример 13. Решить уравнение: х 4 — 15х 2 + 12х + 5= 0.
Решение: Разложим многочлен f(х) = х 4 — 15х 2 + 12х + 5 на множители в следующем виде: 
Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:
Так как , bd = 5, то будем искать решения среди вариантов:
Системе удовлетворяет вариант №2, т.е. а = 3, b = -1, c = -3, d = 5.
Итак,

D =13
D = 29
Ответ:
О решении одного класса кубических уравнений.
Пусть дано кубическое уравнение: а 1 х 3 + b 1х 2 +с 1х +d1 = 0, где а ≠ 0.
Приведём его к виду х 3 + ах 2 +bх + с = 0 (1), где а = 


Положим в уравнении (1) х = у + m. Тогда получим уравнение: 
Раскроем скобки, сгруппируем: y 3 +3у 2 m + 3ym 2 + m 3 + ay 2 + 2aym +am 2 + by +bm + с = 0,
y 3 + y 2 (a +3m) +y(3m 2 +2am +b) + m 3 +am 2 +bm + с = 0.
Для того, чтобы уравнение (1) было двучленным, должно выполняться условие:
Решения этой системы: m = —

Пример14. Решить уравнение: х 3 + 3х 2 +3х — 9 =0.
Решение: В данном уравнении а = 3, в =3, тогда условие a 2 = 3b выполняется, а m = — 
Уравнение принимает вид: (у -1) 3 +3(у -1) 2 +3(у -1) – 9 = 0.
y 3 -3y 2 +3у -1 +3у 2 – 6у +3 +3у –3 – 9 = 0.
y 3 – 10 = 0, откуда у = 

Ответ: 
Пример15. Решить уравнение: х 3 + 6х 2 + 12х + 5 = 0.
Решение: а = 6, в =12, тогда условие a 2 = 3b (62 = 3×12) выполняется, а m = — 
Выполним подстановку х = у — 2. Уравнение принимает вид: (у -2) 3 +6(у -2) 2 +12(у -2) + 5 = 0.
у 3 – 6у 2 + 12у – 8 + 6у 2 -24у + 24 + 12у – 24 + 5 = 0.
у 3 – 3 = 0, у = 

Ответ: 
Рассмотренные в работе примеры могут быть решены и другими способами. Но цель работы заключалась в том, чтобы решить их методом неопределённых коэффициентов, показать универсальность этого метода, его оригинальность и рациональность, не отрицая того, что в некоторых случаях он приводит к громоздким, но не сложным преобразованиям.
http://pandia.ru/text/79/027/66720.php
http://urok.1sept.ru/articles/550924