Решение плохо обусловленных систем линейных алгебраических уравнений

РЕШЕНИЕ ПЛОХО ОБУСЛОВЛЕННЫХ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Приобретение навыков решения плохо обусловленных систем линейных алгебраических уравнений.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим систему линейных алгебраических уравнений.

где А — квадратная матрица размерностью ; —вектор свободных членов;

— искомый вектор

Если , то система (1) называется плохо обусловленной. В этом случае погрешности коэффициентов матрицы и правых частей или погрешности округления при расчетах могут сильно исказить решение.

При решении многих задач правая часть системы (1) и коэффициенты матрицы А известны приближенно. При этом вместо точной системы (1) имеем некоторую другую систему

Полагаем, что величины и d известны.

Так как вместо системы (1) имеем систему (2), то можем найти лишь приближенное решение системы (1). Метод построения приближенного решения системы (1) должен быть устойчивым к малым изменениям исходных данных.

Псевдорешением системы (1) называется вектор , минимизирующий невязку на всем пространстве .

Пусть х 1 –некоторый фиксированный вектор из , определяемый обычно постановкой задачи.

Нормальным относительно вектора х 1 решением системы (1) называется псевдорешение х 0 с минимальной нормой , то есть

где F—совокупность всех псевдорешений системы (1).

Причем

где ¾компоненты вектора х.

Для любой системы вида (1) нормальное решение существует и единственно. Задача нахождения нормального решения плохо обусловленной системы (1) является некорректно поставленной.

Для нахождения приближенного нормального решения системы (1) воспользуемся методом регуляризации.

Согласно указанному методу построим сглаживающий функционал вида

и найдем вектор , минимизирующий на этот функционал. Причем параметр регуляризации a однозначно определен из условия

где .

Вырожденные и плохо обусловленные системы могут быть неразличимы в рамках заданной точности. Но если имеется информация о разрешимости системы (1), то вместо условия (5) следует использовать следующее условие:

Компоненты 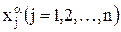вектора являются решениями системы линейных алгебраических уравнений, которая получается из условия минимума функционала (4)

где Е—единичная матрица,

¾эрмитово сопряженная матрица.

На практике для выбора вектора нужны дополнительные соображения. Если их нет, то полагают =0.

Для =0 систему (7) запишем в виде

где

Найденный вектор будет являться приближенным нормальным решением системы (1).

Остановимся на выборе параметра a. Если a=0, то система (7) переходит в плохо обусловленную систему. Если a велико, то система (7) будет хорошо обусловлена, но регуляризованное решение не будет близким к искомому решению системы (1). Поэтому слишком большое или слишком малое a не пригодны.

Обычно на практике проводят расчеты с рядом значений параметра a. Например,

Для каждого значения a находят элемент , минимизирующий функционал (4). В качестве искомого значения параметра регуляризации берется такое число a, для которого с требуемой точностью выполняется равенство (5) или (6).

1. Построить систему линейных алгебраических уравнений, состоящую из трех уравнений с тремя неизвестными, с определителем, величина которого имеет порядок 10 -6 .

2. Построить вторую систему, аналогичную первой, но имеющую другие свободные члены, отличающиеся от свободных членов первой системы на величину 0,00006.

3. Решить построенные системы методом регуляризации (полагая =0 и d=10 -4 ) и каким-либо другим методом (например, методом Гаусса).

4. Сравнить полученные результаты и сделать выводы о применимости использованных методов.

IV. ОФОРМЛЕНИЕ ОТЧЕТА

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. — М.: Наука, 1979. 286 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

О ЧИСЛЕННОМ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННЫМИ МАТРИЦАМИ

О ЧИСЛЕННОМ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННЫМИ МАТРИЦАМИ
Научная статья
Рябов В.М. 1 , Бурова И.Г. 2, *, Кальницкая М.А. 3 , Малевич А.В. 4 , Лебедева А.В. 5 , Борзых А.Н. 6

1 ORCID: 0000-0002-1364-5428;
2 ORCID: 0000-0002-8743-1377;
3 ORCID: 0000-0001-5671-5070;
4 ORCID: 0000-0003-0753-4621;
5 ORCID: 0000-0001-9026-0292;
6 ORCID: 0000-0001-5489-911X;
1, 2, 3, 4, 5, 6 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

* Корреспондирующий автор (i.g.burova[at]spbu.ru)

Аннотация

Представлены результаты численного решения систем линейных алгебраических уравнений (СЛАУ) с симметричными и несимметричными плохо обусловленными матрицами методом регуляризации. Рассматриваются положительно определенные, а также осцилляционные матрицы. В статье показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу A_n системы матрицей где – единичная матрица, а a – некоторое положительное число (параметр регуляризации), которое стремится к нулю.

Ключевые слова: плохо обусловленные системы линейных алгебраических уравнений, матрицы Гильберта, параметр регуляризации.

ON NUMERICAL SOLUTION OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS WITH ILL-CONDITIONED MATRICES
Research article
Ryabov V.M. 1 , Burova I.G. 2, *, Kalnitskaya M.A. 3 , Malevich A.V. 4 , Lebedeva A.V. 5 , Borzykh A.N. 6

1 ORCID: 0000-0002-1364-5428;
2 ORCID: 0000-0002-8743-1377;
3 ORCID: 0000-0001-5671-5070;
4 ORCID: 0000-0003-0753-4621;
5 ORCID: 0000-0001-9026-0292;
6 ORCID: 0000-0001-5489-911X;
1, 2, 3, 4, 5, 6 St. Petersburg State University, St. Petersburg, Russia

* Corresponding author (i.g.burova[at]spbu.ru)

Abstract

The results of the numerical solution of systems of linear algebraic equations (SLAE) with symmetric and asymmetrical ill-conditioned matrices by the regularization method are presented in the paper. Positive-definite and oscillatory matrices are considered. The article shows that in order to regularize the computational process according to the Tikhonov method, it is enough to replace the system matrix A_n with the matrix A_n + αE_n where E_n is the identity matrix, and α is some positive number (regularization parameter) that tends to zero.

Keywords: ill-conditioned systems of linear algebraic equations, Hilbert matrices, regularization parameter.

Введение
При решении различных задач возникает необходимость решать плохо обусловленные СЛАУ с положительно определенными симметричными матрицами. Такие системы линейных алгебраических уравнений возникают, например, когда функцию f (x) аппроксимируют алгебраическими многочленами в метрике пространства : если мы возьмем полином в виде и определим погрешность аппроксимации как то из условия минимизации придем к СЛАУ с матрицей Гильберта. Такие системы линейных алгебраических уравнений также возникают при решении обыкновенных дифференциальных уравнений методом Ритца, что приводит к матрицам Грама. Эти матрицы размерности n являются симметричными и положительно определенными, но при неограниченном увеличении n наименьшее собственное значение может стремиться к нулю, что приводит к неустойчивости решения.
Обычно для получения надежного решения используют методы регуляризации. Общей стратегией является использование стабилизатора Тихонова [1] или его модификаций [2], [3], [4], [5], [6], [7]. В этой статье рассматриваются особенности численного решения СЛАУ с положительно определенной симметричной матрицей с использованием регуляризации. В следующих разделах показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу системы A_n матрицей , где E_n – единичная матрица, а α – положительное число (параметр регуляризации), стремящееся к нулю. Таким образом, мы уменьшаем число обусловленности системы линейных алгебраических уравнений, что увеличивает устойчивость.
Постановка задачи
Пусть A – невырожденная вещественная квадратная матрица порядка n. В этом случае решение СЛАУ Az = f существует и единственно. Известны различные модификации метода Гаусса для решения СЛАУ, например, метод Гаусса с выбором ведущего элемента (в столбце или в матрице) и другие. Предположим, что число обусловленности матрицы A велико, т.е. матрица системы уравнений плохо обусловлена. Решение плохо обусловленных СЛАУ методом Гаусса не всегда дает удовлетворительное решение. Например, пусть
Число обусловленности матрицы A приближенно равно 10 7 . Решая эту систему методом Гаусса без перестановок (с помощью программы, написанной на C++ с вещественными числами типа double), получим z = (1.0? 1.555556, 0.666667) T , что существенно отличается от точного решения (1.0, 1.0, 1.0) T . Подобные примеры были рассмотрены в [6]. Эти примеры показывают, что в процессе решения необходимо избегать деления на малые по абсолютной величине элементы. Избежать эту ситуацию помогает использование модифицированного метода Гаусса, заключающегося в выборе ведущего элемента, являющегося наибольшим по абсолютному значению элементом в столбце (стратегия Уилкинсона) или по всей матрице (стратегия полного упорядочения Жордана) [2]. Применение метода Гаусса с выбором ведущего элемента по столбцам дает решение z = (1.0, 1.0., 1.0) T . Если система уравнений является плохо обусловленной, например, в случае СЛАУ с матрицей Гильберта порядка n с элементами , то практически невозможно получить приемлемое решение СЛАУ с помощью известных методов (прямыми методами, такими как метод Гаусса, метод квадратного корня, итерационными методами и др.).
В таблице 1 приведены числа обусловленности матриц Гильберта порядков от 3 до 20, полученные с помощью пакета Maple (Digits=50). В таблице 2 представлены решения СЛАУ Az = f c матрицами Гильберта H_n, полученные методом Гаусса (стратегия Уилкинсона). Здесь представлены решения, полученные при решении систем уравнений для n= 10, 12, 14, 20, вычисленные в C++ с числами типа double. Решения, представленные в таблице 2, далеки от истинных решений. В следующих разделах представлен метод регуляризации, с помощью которого получены решения исходной системы Az = f с матрицами Гильберта A = H_n при использовании нормы

Численное решение плохо обусловленной системы уравнений
Различные подходы к решению систем уравнений с плохо обусловленными матрицами известны (см. 1). В данной работе для получения приемлемого решения СЛАУ рассматривается применение модификации метода регуляризации. Известный стандартный метод регуляризации Тихонова позволяет найти нормальное решение системы Az = f. Этот метод основан на поиске элемента, на котором функционал достигает наименьшего значения для фиксированного положительного Для этого необходимо решить уравнение Эйлера – сопряженная матрица. Решение уравнения Эйлера зависит от числа обусловленности матрицы A * A . Это число может быть очень большим. Если матрица A симметрична и положительно определена, мы предлагаем найти нормальное решение другим способом. В данной работе предлагается найти нормальное решение путем решения системы уравнений, для которой число обусловленности значительно меньше.
Пусть матрица СЛАУ

является симметричной и положительно определенной (например, матрица Гильберта). В этом случае существует единственный положительно определенный корень из матрицы , т.е. положительно определенная матрица такая, что . Установим связь между собственными значениями и собственными векторами матриц и : пусть µ и собственное значение и собственный вектор матрицы :

Умножив (2) на B, получаем

Используя (2), перепишем (3) как . Это равенство означает, что собственные векторы матриц A и B одинаковы, а собственные значения матрицы A равны квадратам собственных значений матрицы B. Умножив (1) на , получаем

Запишем для (4) уравнение Эйлера для минимизации сглаживающего функционала : оно имеет вид

В случае симметричной матрицы матрица является самосопряженной, поэтому мы получаем уравнение

Формально в исходной системе осуществляется сдвиг, но фактически это метод регуляризации для уравнения (1).
В памяти компьютера числа обычно хранятся с некоторыми погрешностями. Будем считать, что матрица и вектор даны приближенно, т.е. вместо матрицы A и правой части известны такие, что δ. Говорить о сходимости можно лишь при неограниченном увеличении точности исходной информации, т.е. при δ→0. Однако практически мы не можем неограниченно уменьшать δ, из-за чего результаты могут быть далеки от желаемых решений. Решая задачу (6), получаем приближенное решение системы (1).
Замечание. Методы вычисления квадратного корня матрицы описаны в 9. Если матрица A симметрична, нам не нужно вычислять матрицу B. Применение регуляризации непосредственно к уравнению (1) просто увеличит число обусловленности результирующей системы, что невыгодно. В случае несимметричной положительно определенной матрицы уравнение Эйлера для системы (1) имеет вид (5). Сходимость метода регуляризации изложена в [1]. В отличие от стандартного подхода процедуры регуляризации представление (5) имеет меньшее число обусловленности, что очень важно. Но, в отличие от симметричных матриц, необходимо знать матрицу B в случае несимметричной матрицы. Последнее требование усложняет применение данного метода на практике.
Существуют классы несимметричных матриц, все собственные значения которых положительны. Покажем, как в этом случае можно осуществить процесс регуляризации в форме (5), а не в традиционной форме что, как уже упоминалось выше, существенно уменьшает число обусловленности решаемой системы. Рассматривается класс осцилляционных матриц (см. [12]), все собственные значения которых положительны и попарно различны, а соответствующие собственные векторы обладают особыми свойствами колебаний.
Пусть матрица A_n – осцилляционная, а V есть матрица собственных векторов – диагональная матрица собственных чисел A_n. Тогда Пусть _.Положим Понятно, что Таким образом, процесс регуляризации может быть осуществлен в форме (5). Обобщенная матрица Вандермонда, то есть матрица вида … -1 , 10 -2 ,…, 10 -12 для решения возмущенной СЛАУ где матрица исходной системы есть матрица Гильберта порядка n. Решение возмущенной системы получено методом Гаусса с выбором ведущего элемента по столбцам. Точное решение исходной невозмущенной системы H_nz = f есть n-мерный вектор из единиц: z = (1.0, 1.0, …, 1.0) T . Вычисляя решение возмущенной СЛАУ при различных значениях α, находим значение параметра, при котором погрешность решения имеет минимальное значение. Параметр α, соответствующий решению с наименьшей нормой, назовем оптимальным. Таким образом, для решения системы уравнений (1) необходимо решить несколько систем уравнений для различных α. В таблицах 3, 4 полужирным шрифтом выделено наименьшее значение нормы погрешности для заданного n, соответствующее оптимальному значению параметра возмущения α. В последней строке этих таблиц приведены нормы погрешностей решений, полученных без регуляризации. Погрешность решения вычислялась с помощью евклидовой нормы.

Точность арифметики с плавающей запятой можно охарактеризовать машинным ε, т.е. наименьшим положительным числом с плавающей запятой ε, для которого 1 + ε >1 (см. [6]). Мы можем вычислить машинное ε. Например, в 64-битном С++ переменные типа double дают

Теорема Тихонова утверждает, что теоретически, по мере уменьшения α, регуляризованное решение улучшается, но в практических расчетах для достаточно малых α (в пределах точности машины в C++) погрешности округления и число обусловленности матрицы имеют значительное влияние. Это можно увидеть, изучив результаты, представленные в начале таблиц 3, 4.
Заключение
В данной работе представлены результаты численного решения СЛАУ с положительно определенными симметричными (или несимметричными, но почти симметричными) плохо обусловленными матрицами модифицированным методом регуляризации. Показано, что решение СЛАУ с матрицами Гильберта с использованием метода регуляризации может быть существенно улучшено.

Список литературы / References

Научная статья на тему «Решение плохо обусловленных разреженных систем линейных алгебраических уравнений с помощью крыловского подпространства»

Введение. Математические модели многих практических задач приводят к решению СЛАУ с большими и разреженными матрицами коэффициентов, в которых большинство элементов равны нулю. Приписывание матрице свойства разреженности эквивалентно утверждению о существовании алгоритма, использующего её разреженность.

Когда большая доля коэффициентов матрицы состоит из нулей, вполне очевидно, что нам не хотелось бы хранить в памяти компьютера все эти нули. Поэтому матричные алгоритмы должны проектироваться таким образом, чтобы обрабатывались только ненулевые элементы и чтобы на основании предварительного знания о расположении ненулевых элементов избегались операции типа сложения с нулем или умножения на нуль. Таким образом число операций, производимых машиной при исполнении алгоритма, пропорционально числу ненулевых элементов, а не числу всех элементов матрицы. Серьезную проблему при работе с разреженными матрицами представляет численная устойчивость [1, с. 195].

Когда методы типа гауссова исключения требуют слишком много времени или памяти для решения систем уравнений используются итерационные методы. При решении плохо обусловленных разрежен­ных СЛАУ возникает необходимость выбора метода, который позволит получить при решении точный результат и наименьшее заполнение (возникновение новых ненулевых элементов) [3, с. 29]. Наиболее эффективными и устойчивыми среди итерационных методов решения таких систем уравнений являются так называемые проекционные методы, и особенно тот их класс, который связан с проектированием на подпространства Крылова. Эти методы обладают целым рядом достоинств: они устойчивы, допускают эффективное распараллеливание, работу с различными строчными (столбцовыми) форматами и предобуславливателями разных типов.

Рассмотрим систему линейных алгебраических уравнений

, (1)

где: — плохо обусловленная разреженная матрица,

.

В данной работе проводится сравнительный анализ итерацион­ных методов для решения плохо обусловленных разреженных СЛАУ. В качестве исследуемых методов выбраны: метод сопряженных градиентов (CG) , метод минимальных невязок (MinRes), сдвоенный метод сопряженных направлений (CGS), квазиминимальных невязок (QMR) [6, с. 2].

В вопросах выбора того или иного способа решения СЛАУ важно учитывать структуру матрицы A [4, с. 2; 5, с. 47]. Это связано с тем, что не каждый метод дает возможность получить гарантированный результат для определенной системы линейных уравнений.

Таким образом, критерием сравнения итерационных методов решения СЛАУ будут: погрешность результатов, скорость сходимости, структура матрицы.

Результаты численных исследований показали, что для решения СЛАУ с матрицей A являющейся симметричной/несимметричной и хорошо обусловленной к нормальным уравнениям лучше применять метод CG. Если матрица А- симметричная и плохо обусловленная, то лучшую сходимость показал метод MinRes. Для А- несимметрич­ной, плохо обусловленной — метод квазиминимальных невязок [7].

Нужна помощь в написании статьи?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Пишем статьи РИНЦ, ВАК, Scopus. Помогаем в публикации. Правки вносим бесплатно.

Для улучшения скорости сходимости итерационных методов используют предобуславливание матрицы системы. Оно заключается в том, что подбирается такая матрица предообуславливания, что при этом процедура решения СЛАУ является не слишком трудоемкой и численно устойчивой [2, с. 313]. Правильный выбор предобуславливателя, зависящий от конкретной задачи, может в огромной степени ускорить сходимость [9, с. 211]. В действитель­ности, хороший предобуславливатель часто необходим для того, чтобы итерационный метод вообще сходился.

В данной работе было рассмотрено несколько видов предобус­лавливания для метода квазиминимальных невязок с разреженными плохо обусловленными матрицами: левое и правое предобус­лавливание с использованием QR — разложения, левое и правое предобуславливание с использованием LU — разложения, а также с использованием модификации LU — разложения [8, с. 315].

Сравнение относительной погрешности предобуславливателей

В статье был рассмотрен метод квазиминимальных невязок применительно к решению разреженных плохо обусловленных СЛАУ и различные варианты выбора предообуславливателя. Метод квазими­нимальных невязок, основанный на использовании предобуслав­ливателя, полученного с помощью модификации LU- разложения дал наилучший результат по численной устойчивости.

Нужна помощь в написании статьи?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Пишем статьи РИНЦ, ВАК, Scopus. Помогаем в публикации. Правки вносим бесплатно.

1.Голуб Дж., Ван Лоун Ч. Матричные вычисления/ Под ред. В.В. Воеводина. — М.: «Мир», 1999. — 548 с.

2.Деммель Дж. Вычислительная линейная алгебра. Теория и приложения / Пер. с англ.Х.Д. Икрамова. — М.: «Мир», 2001. — 430 c.

3.Писсанецки С. Технология разреженных матриц/ Под ред. Х.Д. Икрамова — М.: «Мир», 1988. — 410 с.

4.Станкевич, И.В. Хранение и использование разреженных матриц в конечно- элементной технологии. Журнал «Наука и Образование». — 2005. — 10 октября.

5.Тьюарсон Р. Разреженные матрицы/ Под ред. Х.Д. Икрамова. — М.: «Мир», 1977. — 172 с.

6.Bucker Martin, Basermann Achim. A comparison of QMR, CGS and TFQMR on a distributed memory machine / Bucker Martin //Mathematics of computation. — 1994 — 31 may

7.Harwell-Boeing Collection — [Электронный ресурс] – Режим доступа. — URL: http://math.nist.gov/MatrixMarket/data/Harwell-Boeing/ (дата обращения: 15.12.2012)

8.Roland W. Freund, Noel M. Nachtigal. QMR: a Quasi-Minimal Residual Method for Non—Hermitian Linear Systems / Roland W. Freund, Noel M. Nachtigal // Journal Math. — 1991. — №60. — p. 315—339.

9.Saad, Y. Iterative methods for sparse linear systems / Y. Saad. // SIAM. — 2003. — 447 p.