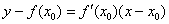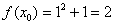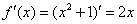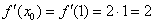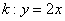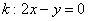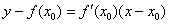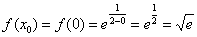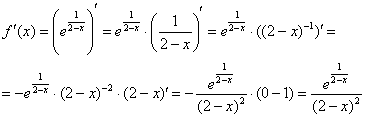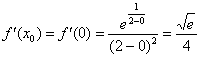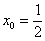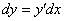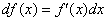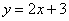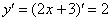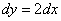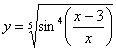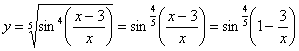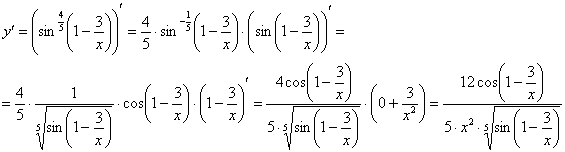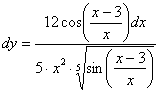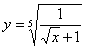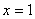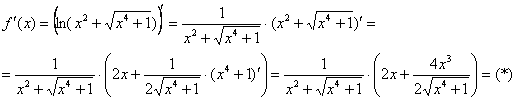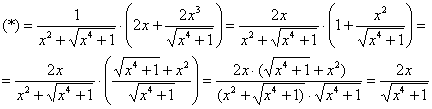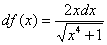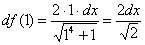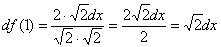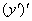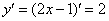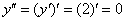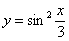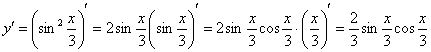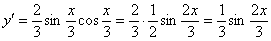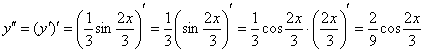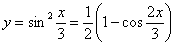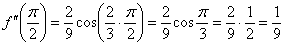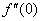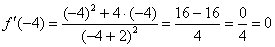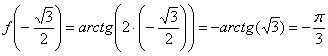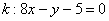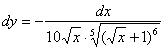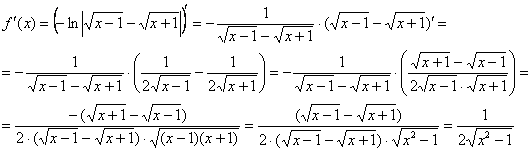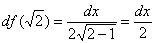Пошаговый калькулятор производных онлайн
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Примеры решения производных с ответами
Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения производных
Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.
Процесс нахождения производный называется дифференцированием.
0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»219″ style=»vertical-align: -5px;» />
0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»180″ style=»vertical-align: -5px;» />
– производная суммы (разницы).
– производная произведения.
– производная частного.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Примеры решений производных
Задача
Найти производную функции
Решение
Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
Ответ
Задание
Найти производную функции
Решение
Обозначим , где
. Тогда, согласно правила вычисления производной сложной функции, получим:
Ответ
Задача
Найти производную функции при
.
Решение
.
.
Ответ
.
Задача
Найти производную функции .
Решение
.
После приведения подобных членов получаем: .
Ответ
Задача
Найти производную функции .
Решение
В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Применяя правила дифференцирования котангенса, получаем: .
Учитывая, что и
, после упрощения получим:
.
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем: .
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем: .
Ответ
.
Задача
Найти производную функции .
Решение
Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты: .
Ответ
.
Задача
Найти производную функции .
Решение
По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.
Ответ
.
Простейшие типовые задачи с производной. Примеры решений
После изучения азов нахождения производной в статьях Как найти производную? Примеры решений и Производная сложной функции мы рассмотрим типовые задачи, связанные с нахождением производной. Желающие улучшить свои навыки дифференцирования также могут ознакомиться с уроком Сложные производные. Логарифмическая производная.
Помимо нового материала у вас есть возможность дополнительно «набить руку» на нахождении производных. Действительно, если речь пойдет о типовых задачах на производную, то, как минимум, во всех примерах нужно будет найти эту самую производную. Я постараюсь рассмотреть приёмы решения и хитрости, которые не встречались в других статьях.
Вот наше аппетитное меню:
Повар на раздаче.
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции 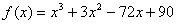
Справка: Следующие способы обозначения функции эквивалентны: 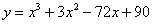
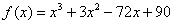
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке 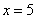
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции 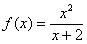
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции 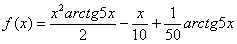
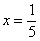
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение 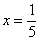
Ну вот, совсем другое дело. Вычислим значение производной в точке 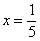
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции 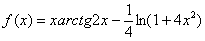
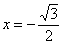
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
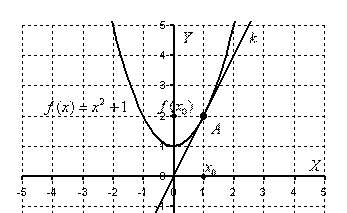
Составить уравнение касательной к графику функции 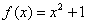
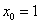
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственной точке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при 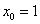
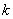
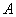
И наша задача состоит в том, чтобы найти уравнение прямой 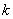
Как составить уравнение касательной в точке с абсциссой  ?
?
Общая формула знакома нам еще со школы:
Значение 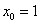
Теперь нужно вычислить, чему равна сама функция в точке 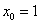
На следующем этапе находим производную:
Находим производную в точке (задание, которое мы недавно рассмотрели):
Подставляем значения 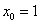
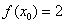
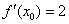
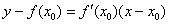
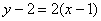
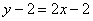
Таким образом, уравнение касательной:
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой на плоскости принято записывать в так называемой общей форме 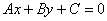
Очевидно, что точка 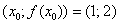
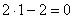
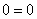
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке 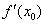
Рассмотрим еще два примера.
Составить уравнение касательной к графику функции 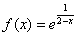
Уравнение касательной составим по формуле
1) Вычислим значение функции в точке 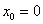
2) Найдем производную. Дважды используем правило дифференцирования сложной функции:
3) Вычислим значение производной в точке 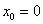
4) Подставим значения 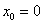
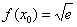
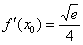
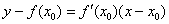
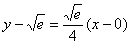
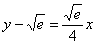
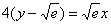
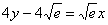
Выполним частичную проверку:
Подставим точку 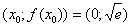
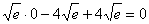
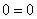
Составить уравнение касательной к графику функции 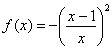
Полное решение и образец оформления в конце урока.
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду. И, конечно же, ознакомьтесь со строгим определением касательной, после чего закрепите материал на уроке Уравнение нормали, где есть дополнительные примеры с касательной.
Дифференциал функции одной переменной
С формально-технической точки зрения найти дифференциал функции – это «почти то же самое, что найти производную».
Производная функции чаще всего обозначается через 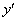
Дифференциал функции стандартно обозначается через 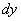
Дифференциал функции одной переменной записывается в следующем виде:
Другой вариант записи:
Простейшая задача: Найти дифференциал функции
1) Первый этап. Найдем производную:
2) Второй этап. Запишем дифференциал:
Дифференциал функции одной или нескольких переменных чаще всего используют для приближенных вычислений.
Помимо «комбинированных» задач с дифференциалом время от времени встречается и «чистое» задание на нахождение дифференциала функции:
Найти дифференциал функции
Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё до дифференцирования? Смотрим на наш пример. Во-первых, можно преобразовать корень:
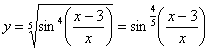
Во-вторых, замечаем, что под синусом у нас дробь, которую, очевидно, предстоит дифференцировать. Формула дифференцирования дроби очень громоздка. Нельзя ли избавиться от дроби? В данном случае – можно, почленно разделим числитель на знаменатель:
Функция сложная. В ней два вложения: под степень вложен синус, а под синус вложено выражение 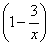
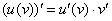
Запишем дифференциал, при этом снова представим 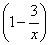
Когда производная представляет собой дробь, значок 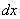
Найти дифференциал функции
Это пример для самостоятельного решения.
Следующие два примера на нахождение дифференциала в точке:
Вычислить дифференциал функции 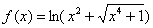
Найдем производную:
Опять, производная вроде бы найдена. Но в эту бодягу еще предстоит подставлять число, поэтому результат максимально упрощаем:
Труды были не напрасны, записываем дифференциал:
Теперь вычислим дифференциал в точке 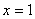
В значок дифференциала 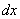
Ну и хорошим тоном в математике считается устранение иррациональности в знаменателе. Для этого домножим числитель и знаменатель на 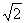
Вычислить дифференциал функции 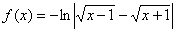
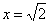
Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.
Вторая производная
Всё очень просто. Вторая производная – это производная от первой производной:
Стандартные обозначения второй производной: 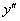
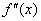
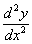
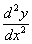
Рассмотрим простейший пример. Найдем вторую производную от функции 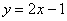
Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
Теперь находим вторую производную:
Рассмотрим более содержательные примеры.
Найти вторую производную функции
Найдем первую производную:
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу 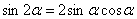
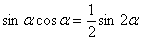
Находим вторую производную:
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу 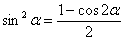
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке 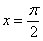
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.
Найти вторую производную функции 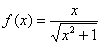
Это пример для самостоятельного решения.
Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но встречаются чуть реже.
Решения и ответы:
Пример 2: Найдем производную: 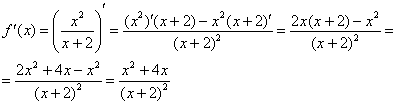
Вычислим значение функции в точке 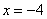
Пример 4: Найдем производную: 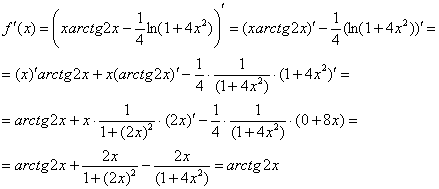
Вычислим производную в заданной точке:
Пример 6: Уравнение касательной составим по формуле 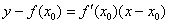
1) Вычислим значение функции в точке 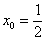
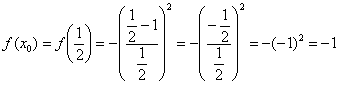
2) Найдем производную. Перед дифференцированием функцию выгодно упростить: 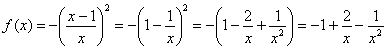
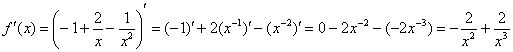
3) Вычислим значение производной в точке 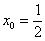
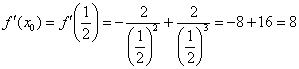
4) Подставим значения 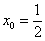
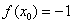
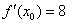
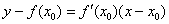
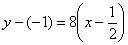
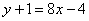
Пример 8: Преобразуем функцию: 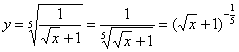
Найдем производную: 
Запишем дифференциал:
Пример 10: Найдем производную:
Запишем дифференциал: 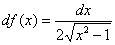
Вычислим дифференциал в точке 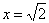
Пример 12: Найдем первую производную: 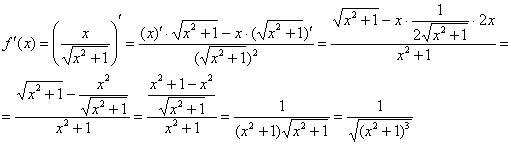
Найдем вторую производную: 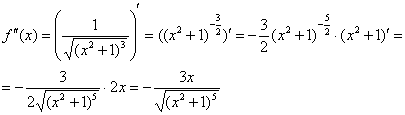
Вычислим:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
http://nauchniestati.ru/spravka/primery-resheniya-proizvodnyh/
http://mathprofi.net/tipovye_zadachi_s_proizvodnoi.html
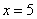
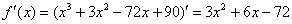
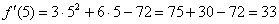
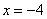
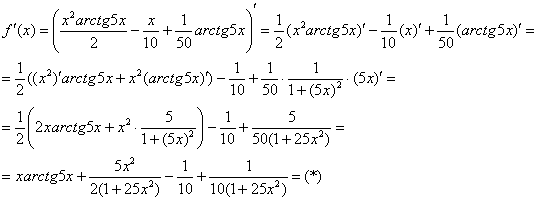
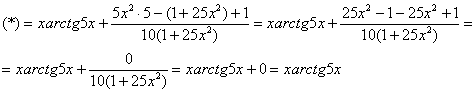
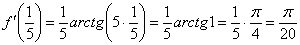
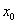 ?
?