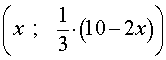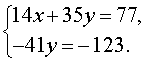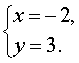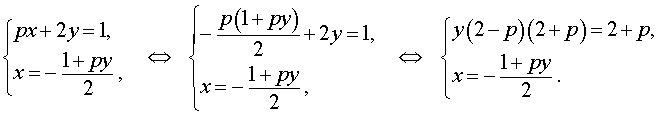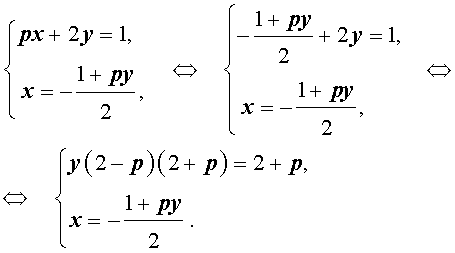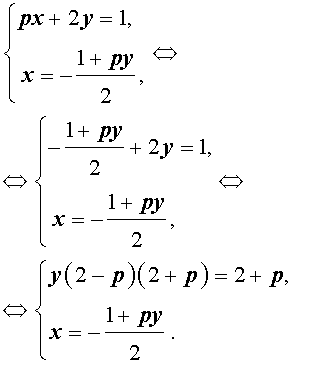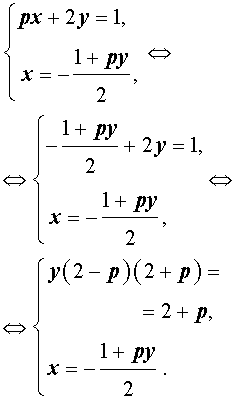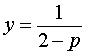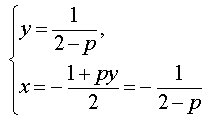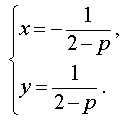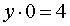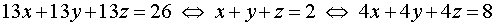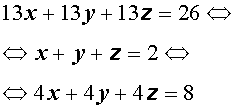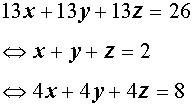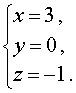Решение простейших систем содержащих уравнение первой степени

Решение систем, содержащих одно уравнение первой степени, другое второй.
презентация к уроку (алгебра, 8 класс) по теме

Данный урок алгебры проводится в 8 классе. Итоговый урок при изучении темы решение систем уравнений. К презентации даются разноуровневые самостоятельные работы.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

1. Уравнением какого вида задаётся квадратичная функция?

И) у=х 3 У) у=5х+3 М) у=5х 2

2. График квадратичной функции называется:

С) квадрат У) гипербола И) парабола

З. Графический способ решения систем уравнений заключается:

М) в построении графиков функций разными цветами;

Н) в построении графиков функций в одной системе координат;

У) в построении графиков функций в разных системах координат.

4. Вершина параболы, заданной уравнением у = (х-3) 2 +4, находится в точке с координатами:

5. Сколько способов решения систем уравнений существует?

Предварительный просмотр:

г. Армавир, 2005г.

Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три – четыре различные задачи. Решая одну задачу различными способами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.

— воспитательная задача: воспитание культуры поведения на уроке и стиля общения с учителем, одноклассниками;

— развивающая задача: развитие самостоятельности учащихся в обучении;

— обучающая задача: овладение методами (способами) решения систем уравнений, содержащих одно уравнение первой, другое второй степени.

1. Устная работа.
2. Работа по карточкам.
3. Фронтальный опрос.
4. Задание на дом.
5. Работа в тетрадях (по группам).
6. Защита работ (по группам).
7. А ну-ка, разгадай!
8. Работа в тетрадях (индивидуальная).
9. Взаимоконтроль.
10. Самостоятельная работа по уровням.

11. Проверка самостоятельной работы.

1. Мультимидийный проектор.
2. Презентация.
3. Компьютеры.
4. Тетради.
5. Доска.
6. Мел.
7. Цветные маркеры.
8. Половинки ватмана для защиты групповых работ.
9. Листики для выполнения самостоятельной работы.
10. Раздаточный материал для самостоятельной работы по трём уровням.
11. Цветные треугольники (зелёные и красные).

1. Приветствуются учащиеся, гости урока. Сообщается тема урока (Слайд №1).

1. Учащиеся знакомятся с содержанием эпиграфа и триединых задач урока

1. Проводится устная работа с учащимися, содержащая два задания: вычислить и охарактеризовать данную функцию по уравнению (Слайд №3).

Перед тем как начать устную работу шести ученикам выдаются карточки, после выполнения первого задания устной работы карточки передаются тем учащимся, которые их будут проверять. По окончании устной работы карточки сдаются учителю.

1. Проводится фронтальный опрос по теории, соответствующей теме урока

1. Демонстрируются определения и комментируются ещё раз учителем ответы на вопросы фронтального опроса. (Слайд №5)

Учителем задаётся вопрос учащимся: Кто из вас подобрал высказывания, касающиеся темы сегодняшнего урока и тех вопросов, что были заданы?

1. Задаётся домашнее задание, содержание которого должно соответствовать уровню знаний каждого ученика. Оформить выполненное домашнее задание необходимо на половинке листа А4 формата (Слайд №6).

1. Работа в тетрадях. Учащиеся разбиваются на группы: 1 группа: 1 и 2 стол, 2 группа: 3 и 4 стол, 3 группа: все остальные. Учащимся предлагается решить одну систему уравнений тремя способами. Первой группе – методом подстановки, второй группе – методом сложения, третьей – графическим способом (Слайд № 7).

Каждая группа при этом должна оформить решение системы уравнений на половинке листа ватмана.

8. Представитель от каждой группы выходит с проектом решения и защищает работу группы. Параллельно на экран выводится решение системы тем или иным методом с выполнением требований к оформлению письменных работ.

Метод сложения (Слайд №8)

Графический способ (Слайд №9)

1. После того как все группы защитили свои проекты решений системы – разминка (Слайд № 10).

Разгадывая ребус, учащиеся должны ответить на вопрос: «Что, по вашему мнению, здесь лишнее и почему?» (Ответ: среди слов кубическая парабола, гипербола, кривая, парабола, прямая лишнее кривая.)

1. Далее учащиеся продолжают работу в тетрадях. В тетради переписывается условие всех пяти систем уравнений. Вниманию учащихся предлагается решить пять систем уравнений: первому столу – первую, второму столу – вторую, третьему столу – третью, четвёртому столу – четвёртую, а учащимся, сидящим по периметру класса – пятую (Слайд № 11).

1. По мере выполнения задания учащиеся, сидящие за разными столами (первый – второй, третий – четвёртый, а по периметру друг с другом) обмениваются тетрадями и производят взаимоконтроль, сверяя правильность решения с экраном и выставляя отметки (Слайд № 12).

1. Учащимся, сидящим за компьютером, предлагается на выбор три уровня самостоятельной работы. Тем, кто сидит за рабочими столами без компьютера, на бумажном носителе предлагается самостоятельная работа, соответствующая уровню их знаний. Те из учащихся, кто хочет повысить отметку, выполняет самостоятельную работу сначала на Первый уровень, затем на Второй уровень и Третий – последовательно. На розданных листах ответов каждый ученик заготавливает таблицу: (Слайд № 13)

Алгебра. 7 класс

Конспект урока

Решение задач при помощи систем уравнений первой степени

Перечень рассматриваемых вопросов:

• Решение системы уравнений.

Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Решить систему – это значит найти все её решения.

Алгебраический способ состоит в получении ответа на вопрос задачи с помощью составления уравнения или системы уравнений и последующего решения уравнения или системы.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Рассмотрим задачу. Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?

Мы не знаем, сколько овец у Ивана, и сколько у Петра.

Обозначим за х число овец у Ивана, а за у – число овец у Петра.

Мысленно разделим условие задачи на две независимые части:

1. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»

2. А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»

Для каждой из частей составим уравнение с двумя неизвестными.

Начнем с первой части.

Если бы Пётр отдал Ивану одну овцу, то у Петра осталось бы (у – 1) овец.

А у Ивана стало бы (х + 1) овец.

Но тогда у Ивана было бы вдвое больше овец, чем у Петра.

Можем составить уравнение x + 1 = 2(y – 1).

Составим уравнение с двумя неизвестными для второй части. Если бы Иван отдал Петру 1 овцу, то у Ивана осталось бы (x – 1) овец. А у Петра стало бы (y + 1) овец, и тогда они имели бы овец поровну. Можем составить уравнение: x – 1 = y + 1

Мы составили два уравнения.

И в первом и во втором уравнении х обозначает число овец у Ивана, а у – число овец у Петра. Другими словами, каждое неизвестное число обозначает одно и то же в обоих уравнениях. Значит, эти уравнения можно рассматривать совместно, то есть объединить их в систему уравнений:

Решим эту систему способом подстановки.

Раскроем скобки в правой части первого уравнения.

Выразим х через у.

Подставим (2у – 3) вместо х во второе уравнение системы. Получим уравнение с одним неизвестным у.

Решим его. Упростим левую часть уравнения.

Перенесем неизвестные в левую часть. уравнения, а числа – в правую.

Подставим у = 5 в первое уравнение.

Система имеет единственное решение: х = 7, у = 5.

Вернемся к исходным обозначениям.

Получаем, что у Ивана было 7 овец, а у Петра 5 овец.

Таким образом, мы решили задачу при помощи системы уравнений первой степени.

Задачи с помощью системы уравнений можно решать по следующей схеме.

Сначала вводим обозначения неизвестных.

Мысленно разделив условие задачи на две части, составляем 2 уравнения и объединяем их в систему.

Решаем полученную систему уравнений.

Возвращаемся к условию задачи и использованным обозначениям.

Отбираем решения и записываем ответ.

Разбор заданий из тренировочного модуля.

1. Решим задачу алгебраическим способом.

Даны 3 числа, сумма которых равна 23. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится 32. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.

В задаче 3 неизвестные, поэтому введем следующие обозначения:

Пусть х – первое число, у – второе число, z – третье число.

Мысленно разделим условие задачи на 3 части, по каждой из которых составим уравнение с тремя неизвестными:

Вернёмся к условию задачи: первое число 15, второе число 5, третье число 3.

Составим систему уравнений по условию задачи.

В трех сосудах 54л воды. Если из первого перелить во второй сосуд 4л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17л, то во втором сосуде окажется в 4 раза больше воды, чем в третьем. Сколько воды в каждом сосуде?

Пусть x л воды было в первом сосуде, y л воды – во втором, z воды – в третьем. Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.

Когда из первого сосуда перелили 4 л воды во второй сосуд, то во втором сосуде стало y + 4 л воды, а в первом сосуде x – 4 л воды. По условию задачи воды стало в сосудах поровну. Составляем уравнение:

Если из третьего сосуда перелить во второй 17 л, то в третьем останется z – 17 л, а во втором станет y + 17 л. По условию задачи во втором сосуде окажется в 4 раза больше воды, чем в третьем. Можем составить уравнение: y + 17 = 4(z – 17).

Записываем систему уравнений:

2. Система уравнений по условию задачи.

Составим систему уравнений по условию задачи: 5% одного числа и 4% другого вместе составляют 46, а 4% первого числа и 5% второго вместе составляют 44. Найдите эти числа.

Системы линейных уравнений

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Системы из двух линейных уравнений с двумя неизвестными

Системы из трех линейных уравнений с тремя неизвестными

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

Решение . Выразим из равенства (2) переменную y через переменную x :

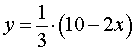(3)

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

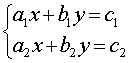(4)

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

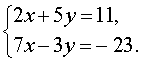(5)

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

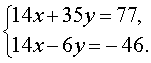(6)

Теперь совершим над системой (6) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

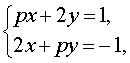(7)

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

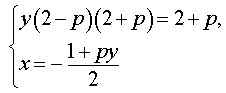(8)

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

,

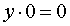
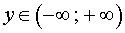
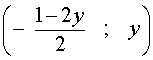
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

,

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

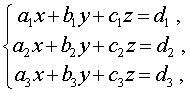(10)

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

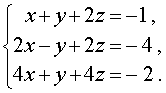(11)

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

• первое уравнение системы оставим без изменений;
• ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
• из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

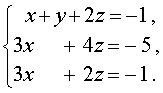(12)

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

• первое и второе уравнения системы оставим без изменений;
• из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

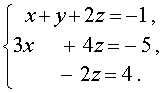(13)

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

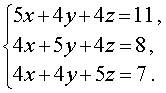(14)

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».