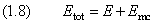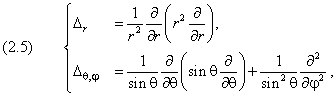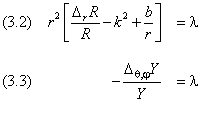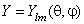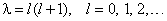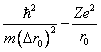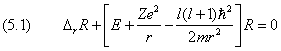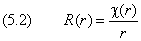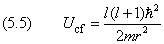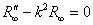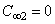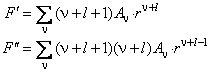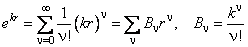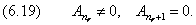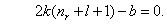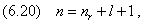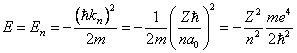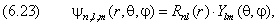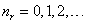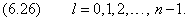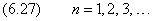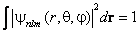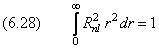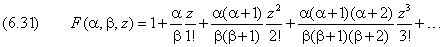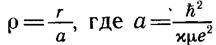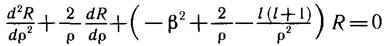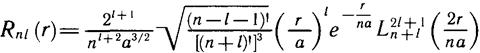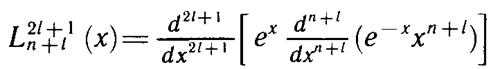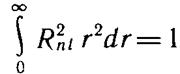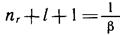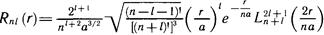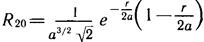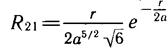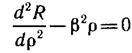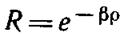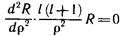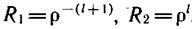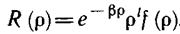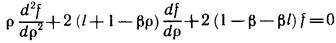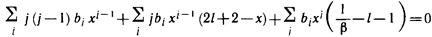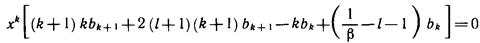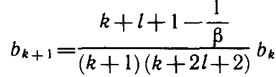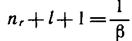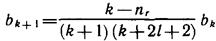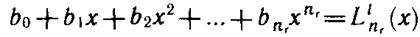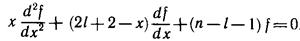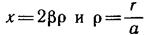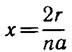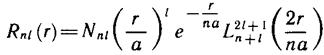Решение радиального уравнения для атома водорода

Решение радиального уравнения для атома водорода

Выпишем уравнение для радиальной части волновой функции R(r)

, ( 1 )

которое предстоит решить. Введем обозначения

, ( 2 )

в которых мы учли, что рассматриваем связанные состояния ( E 0. Такое решение неприемлемо для волновой функции. Значит суммирование в (6) и последующих формулах начинается с k = 1. Суммируем все коэффициенты при произвольной степени r k и приравниваем нулю

. ( 10 )

Найдем отношение коэффициентов

. ( 11 )

При больших k это отношение стремится к

. ( 12 )

Немного отвлечемся и рассмотрим разложение в ряд экспоненты

. ( 13 )

Отношение последующего коэффициента разложения к предыдущему совпадает с (12)

. ( 14 )

Отсюда вывод: функция U(r) в общем случае (для произвольных значений β) расходится при больших r.

Чтобы этого избежать, ограничим ряд. Пусть при некотором k = n

. ( 15 )

. ( 16 )

Из уравнения (15) находим возможные значения β, вспоминаем, что в выражение β входит энергия E и получаем

. ( 17 )

Приведем выражения для первых двух волновых функций

.

. ( 18 )

Значения коэффициентов a₁ и a₂ определяют из условия нормировки волновых функций. Окончательные выражения волновых функций атома в основном состоянии (n = 1) и первом возбужденном (n = 2) приведены в тексте лекции. Итак, если мы хотим получить решение, удовлетворяющее требованиям к волновой функции, необходимо допустить квантование энергии атома.

Решение радиального уравнения для атома водорода

В этой главе излагается решение уравнения Шредингера в рамках задачи Кеплера. Мы убедимся, что без учёта релятивистских эффектов положение энергетических уровней получается таким же, как и в теории Бора–Зоммерфельда, но определяемая волновой функцией форма орбиталей в квантовой теории отличается от классических траекторий. В случае кулоновского поля существуют аналитические выражения для волновых функций, что позволяет вычислить средние значения физических параметров и, например, получить представление о размерах атома в различных состояниях.

Анализ задачи с позиций квантовой механики позволяет выяснить природу основного состояния любого атома, понять причину сгущения уровней вблизи границы ионизации, а также дать ответ на вопрос о вырождении энергетических уровней. Квантовые числа углового момента, которые определяют структуру волновой функции, необходимы при классификации спектров сложных атомов, для которых аналитическое решение уравнения Шредингера невозможно.

Проблема атома водорода и, в особенности, водородоподобных ионов с большим зарядом ядра, требует учёта релятивистских эффектов. Один из них — зависимость массы электрона от скорости — в главе 13 рассмотрен в классическом приближении. Мы увидели, что при переходе к тяжёлым атомам этот эффект растёт быстро, пропорционально Z 4 , но, тем не менее, остаётся малым вплоть до элементов группы железа. Аналогичными свойствами обладает спин–орбитальное взаимодействие. Его роль заключается в снятии вырождения уровней, характерного для нерелятивистской модели атома. Задача о кулоновском поле имеет аналитическое решение и в релятивистском случае. Но для атомов вплоть до элементов группы железа оба упомянутых эффекта малы по сравнению с электростатическим взаимодействием и могут быть рассмотрены как малые поправки к полученным в этой главе формулам.

16.1 Приведённая масса

Рассмотрим взаимодействие двух заряженных частиц по закону Кулона. С потенциальной энергией (13.3.3) стационарное уравнение Шредингера для волновой функции системы ψ_SYS имеет вид

.

Здесь r_e и r_Z —радиус–векторы, соответственно, электрона и ядра, E_tot — полная энергия системы. Введём положение центра инерции частиц

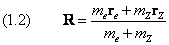
и электрона относительно ядра

.

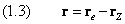
Две последние формулы соответствуют определениям (13.2.3) и (13.2.4) классической механики. Выполним замену переменных в операторах дифференцирования в левой части (1.1):

Подставив (1.4) в (1.1), приходим к уравнению

.

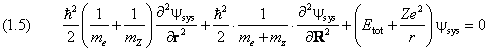
Оно допускает разделение переменных. Представим волновую функцию в виде произведения

,

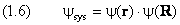
где первый множитель не зависит от R, а второй — от r. Разделим (1.5) на ψ_SYS и второе слагаемое слева перенесём в правую часть:

.

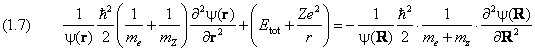
Левая и правая части последнего уравнения зависят от разных переменных, поэтому каждая из них должна быть равна константе. Полная энергия E_tot системы складывается из её внутренней энергии E и энергии E_mc движения центра масс электрона и ядра:

,

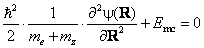
описывает равномерное прямолинейное движение центра масс, а уравнение

есть искомое уравнение Шредингера для относительного движения. Как и в классической механике, задача сводится к движению вокруг ядра частицы, занимающей место электрона, но масса её равна приведённой массе системы (13.2.6).

16.2. Новые параметры

В связанном состоянии энергия частицы E, как известно, отрицательна. Вместо неё будем пользоваться «дебройлевским» волновым числом:

.

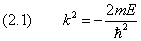
Введём масштаб длины
.

Напомним, что a₀ — боровский радиус (1.2.7). В этих обозначениях уравнение (1.9) приобретает следующий вид:

.

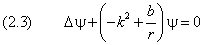
Удобно перейти к сферическим координатам, в которых оператор Лапласа равен сумме

,

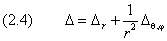
называются, соответственно, «радиальным» и «угловым» лапласианом. Напомним, что угловой лапласиан, согласно (12.5.1), с точностью до знака равен оператору квадрата момента количества движения l 2 . Перейдём к решению задачи.

16.3. Разделение сферических переменных

Покажем, что в сферических координатах задача допускает дальнейшее разделение переменных. Волновую функцию ищем в виде произведения

.

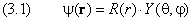
Подставим (3.1) в (2.3), разделим полученное уравнение на ψ(r) и перенесём в правую часть слагаемое с оператором, действующим на угловые переменные:

.

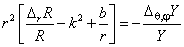
Слева и справа от знака равенства стоят функции от разных аргументов. Следовательно, обе они равны одной и той же константе:

Уравнение (3.3) совпадает с (12.5.3) и, таким образом, представляет собой задачу на собственные значения квадрата момента. Согласно (12.5.5) и (12.6.2), она имеет ограниченное и однозначное решение

Подставляя это значение λ в (3.2), получим обыкновенное дифференциальное уравнение для радиальной части волновой функции:

.

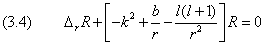
Прежде, чем приступить к его решению, проведём качественные исследования некоторых свойств радиального движения.

16.4. Свойства движения в кулоновском поле

Наличие основного состояния и сгущение уровней вблизи границы ионизации — оба этих свойства кулоновского поля являются следствием соотношения неопределённостей.

Рассмотрим волновую функцию электрона, локализованного внутри малой сферы радиуса r₀. Неопределённость в значениях его координат приблизительно равна r₀, неопределённость в значении импульса, соответственно, порядка ħ/r ₀ , а среднее значение кинетической энергии T составляет ħ 2 /mr ₀ 2 . Полная энергия, равная сумме
,

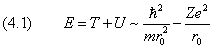
не может неограниченно убывать по мере уменьшения r₀. Следовательно, дискретный спектр начинается с некоторого отрицательного конечного значения. Иными словами, в кулоновском поле имеется основное состояние.

Этот результат отличается от движения в потенциальной яме бесконечной глубины, где отрицательная энергия дискретных уровней неограниченно растёт по абсолютной величине. Различие обусловлено степенью крутизны потенциальной функции. Если в (4.1) вместо кулоновского потенциала подставить, например

с достаточно большим показателем степени:

то энергия E при уменьшении r₀ становится отрицательной, неограниченно увеличиваясь по абсолютной величине. Но если средняя энергия может принимать такие значения, то это означает, что существуют сколь угодно глубокие уровни. Потенциальная яма имеет стенки, более крутые, чем любаястепеннáя функция, следовательно, её уровни энергии действительно не должны иметь нижней границы.

Ещё раз обратим внимание на то, что существование основного состояния атома является чисто квантовым явлением. В классической механике при равном нулю моменте обязательно имеет место падение электрона на ядро.

Теперь исследуем характер энергетического спектра электрона, находящегося на больших расстояниях от ядра. Рассмотрим волновой пакет, «заполняющий» шаровой слой большого радиуса r₀ и толщины Δr r₀. Тогда порядок величины кинетической энергии будет ħ 2 / m( Δr ) 2 . Теперь увеличиваем r ₀ и, пропорционально ему, Δr ₀ . Для электрона в кулоновском потенциале при достаточно больших значениях r ₀ сумма

(4.2)

станет отрицательной. Таким образом, существуют стационарные состояния с отрицательной энергией, в которых частица может находиться на больших расстояниях от ядра. Но это означает, что существуют сколь угодно малые по абсолютной величине уровни энергии. Иными словами, дискретный спектр содержит бесконечно много уровней, сгущающихся к границе ионизации. Снова мы видим кардинальное отличие от решения задачи о потенциальной яме. Причина та же: большая крутизна потенциальной функции. Из (4.2) легко убедиться, что в случае α>2 никакого сгущения уровней ожидать не приходится.

По сути дела, мы убедились, что у каждой атомной системы есть основное состояние с конечным значением энергии, и её уровни сгущаются по мере приближения к границе ионизации. Оба эти заключения следуют из того, что потенциальная функция любого иона и атома близка к закону Кулона как вблизи ядра, так и на очень больших расстояниях от него. Вблизи ядра можно пренебречь влиянием электронов, и потенциальную энергию (отрицательную) описывает формула Ze 2 / r. Вдали от него справедлива изложенная в разделе 13.8 модель атомного остатка. Потенциальная энергия оптического электрона в этой модели также описывается законом Кулона и пропорциональна отношению (Z–N+1)e 2 / r, где N — число электронов в ионе или атоме.

16.5. Эффективный потенциал

Покажем, что решение радиальной части (3.4) волнового уравнения не имеет вырождения. На время вернёмся к обозначениям первого раздела. Вынесем за скобки множитель 2m / ħ 2 и с учётом (2.1) и (2.2) получим:

(5.1) приводится к виду

.

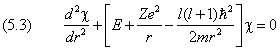
Последнее уравнение описывает одномерное движение в поле с потенциальной энергией

.

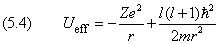
На первом месте здесь стоит потенциальная энергия электрона. Числитель второго слагаемого равен собственному значению квадрата момента. В связи с этим величину

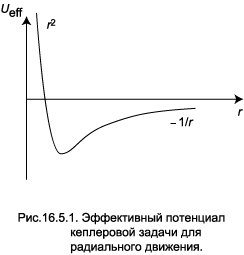
в квантовой теории, как и в классической механике, принято называть «центробежным потенциалом», а сумму (5.4) — «эффективным потенциалом». Профиль эффективного потенциала схематически изображён на рис.16.5.1.

На больших расстояниях от ядра превалирует кулоновский потенциал, а на малых — центробежный. Поэтому эффективный потенциал имеет минимум. Его зависимость от r напоминает яму конечной глубины, но в отличие от ямы здесь пологие края.

Уравнение (5.3) показывает, что задача о радиальном движении в кулоновском поле сводится к задаче об одномерном движении в области, ограниченной с одной стороны. Как показано во втором разделе девятой главы, ограниченное одномерное движение является невырожденным. Отсюда следует заключение об отсутствии вырождения по радиальной координате и в случае кулоновского поля. Таким образом, вырождение волновой функции кулоновского поля обусловлено исключительно её угловой частью.

Перейдём к определению энергетических уровней, поставив условие ограниченности волновой функции.

16.6. Вычисление радиальной части волновой функции

Раскроем радиальную часть лапласиана Δ_r:

.

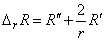
Подставив полученное выражение в (3.4), приходим к уравнению

.

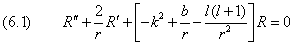
Его, как и уравнение, описывающее линейный осциллятор, решаем методом разложения в ряд с предварительным выделением особых точек.

Особые точки

В рассматриваемой здесь задаче присутствуют две особые точки: бесконечно удалённая точка r→∞ и начало координат r=0 . Введём обозначения R_∞ для волновой функции на больших расстояниях от ядра и R₀ — вблизи него. Для выяснения зависимости R_∞(r) опустим в (6.1) все слагаемые, содержащие в знаменателе r. Получающееся в результате уравнение

.

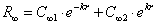
Из условия ограниченности волновой функции вытекает требование

и окончательно приходим к результату

.

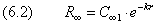
Поведение волновой функции вблизи ядра определяется как раз теми слагаемыми, которые мы опустили при поиске R_∞. Предположим, что орбитальный момент отличен от нуля: l>0 . Тогда в квадратных скобках (6.1) можно пренебречь первым и вторым членами по сравнению с центробежным потенциалом:

.

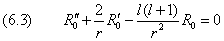
Решение последнего уравнения ищем в виде степеннóй функции

,

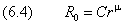
для которой надо найти значение показателя степени μ. После подстановки (6.4) в (6.3) приходим к квадратному уравнению для μ:

,

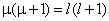
два корня которого равны:

.

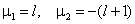
Таким образом, решением уравнения (6.3) является линейная комбинация

.

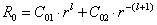
Из требования ограниченности волновой функции следует

.

.

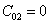
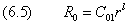
В случае l=0 уравнение (6.3) имеет решение

что формально не противоречит (6.5).

Итак, формулы (6.2) и (6.5) описывают поведение волновой функции, соответственно, в бесконечно удалённой точке и вблизи начала координат.

Разложение в ряд

Решение для произвольного диапазона радиальной координаты будем искать в виде

,

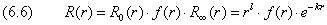
причём константы C ₀₁ и C_{∞ 1} из (6.5) и (6.2) включены в искомую функцию f(r). Её мы представляем в виде ряда

.

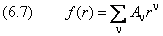
Запишем выражение для радиальной функции:

.

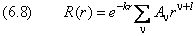
Исключим из исходного уравнения (6.1) слагаемое с первой производной. Для этого выполним замену переменной:

.

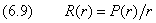
Функция P(r) может быть разложена в ряд аналогично (6.8):

Оператор Лапласа, применённый к функции P(r), содержит только вторую производную:

.

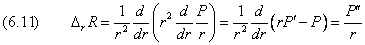
Теперь перепишем уравнение (6.1) в виде:

.

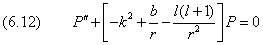
Подставим в него P(r) из (6.10a) и получим уравнение для функции F(r):

.

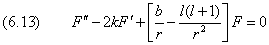
Дважды дифференцируя ряд (6.10b): (6.10),

и подставляя его в (6.13), получим бесконечную систему уравнений для коэффициентов разложения:

Увеличим на единицу индекс суммирования в первом и последнем членах суммы, после чего вынесем за скобки общий множитель r ν+l :

.

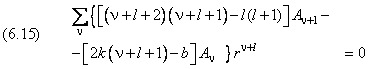
Поскольку последнее равенство выполняется при произвольных значениях переменной r, коэффициенты при всех степенях r ν+l должны быть равны нулю. Отсюда следует рекуррентное соотношение:

.

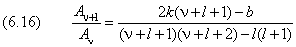
Задав значение A ₀ , мы можем вычислить коэффициент разложения с любым номером.

Только конечная сумма даёт ограниченное решение

Покажем, что, как и в случае линейного осциллятора (глава 11), условию ограниченности волновой функции R(r)удовлетворяет только конечная сумма, но не бесконечный ряд. Для этого достаточно убедиться, что такой ряд растёт быстрее, чем e kr . В самом деле, при неограниченном возрастании номера ν отношение коэффициентов ряда (6.16) стремится к пределу

.

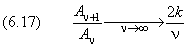
А в разложении экспоненты:

отношение коэффициентов равно

.

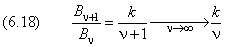
Сравнение (6.17) и (6.18) показывает, что в случае бесконечного ряда волновая функция R(r) не стремится к нулю при неограниченном удалении от ядра. Физический смысл имеет только решение уравнения (6.13) в виде конечной суммы.

Условие квантования энергии

В конечной сумме существует номер ν=n_r такой, что

Параметр n_r называется радиальным квантовым числом. Он аналогичен введённой в предыдущей главе величине n_r и, как мы увидим ниже, принимает тот же ряд значений (15.1.23). Согласно (6.16) и (6.19), решение существует только в том случае, если k удовлетворяет условию

Таким образом, волновое число электрона квантуется: оно определяется линейной комбинацией

называемой главным квантовым числом. Снова прослеживается аналогия с классической моделью атома: (6.20) получается из (15.1.11) заменой n_φ на l+1. Эта замена обусловлена принципиально разной интерпретацией состояний с равным нулю моментом в квантовой теории и классической механике. Выпишем в явной форме правило квантования волнового числа:

.

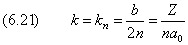
Из соотношений (2.1) и (6.21) получим условие квантования энергии:

или, вспоминая определение ридберга (13.5.3):

Эта формула даёт собственные значения нашей задачи. Собственные функции (волновые функции) зависят от трёх координат (r, θ, φ) и трёх параметров (n, l, m):

где Y_lm — угловая часть волновой функции, R_nl — радиальный множитель, равный

.

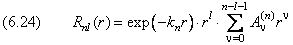
Коэффициенты суммы связаны друг с другом рекурренным соотношением

.

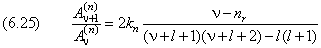
Сумма в (6.24) является знакопеременной. В этом легко убедиться, заметив, что числитель дроби (6.25) имеет отрицательный знак.

К радиальной волновой функции применима осцилляционная теорема, о которой шла речь в разделе 9.3. Число узлов функции R_nl равно квантовому числу n_r.

Уточним диапазон изменения квантовых чисел n, n_r и l. Согласно (12.1), параметр l должен быть неотрицательным. Нумерация слагаемых под знаком суммы в (6.24) начинается с нуля, поэтому n_r принимает целые значения:

Энергетический уровень однозначно определяется главным квантовым числом n. Из (6.20) следует, что при заданном значении n орбитальное квантовое число может быть равно одному из чисел ряда:

Если в (6.20) равны нулю оба параметра: 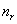и l , — то n равно единице. Остальным парам чисел соответствуют б óльшие значения n . Итак:

Обратим внимание на то, что орбитальное квантовое число выпало из окончательного результата (6.22), хотя в уравнении Шредингера (6.1) оно присутствует. Этот факт является следствием особо высокой степени симметрии кулоновского поля — более высокой, чем просто поле с центральной симметрией. В общем случае центрально-симметричного поля, потенциал которого падает по закону, отличному от 1/r, энергия зависит от квантового числаl.

Нормированная волновая функция

Разложение (6.23) волновой функции на множители, каждый из которых зависит либо от радиальной, либо от угловых координат, позволяет разбить общее условие нормировки

на два: по радиальной координате

.

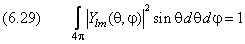
Для справочных целей выпишем полные выражения для нормированных волновых функций. Сумма в (6.24) с рекуррентным соотношением (6.25) для коэффициентов может быть выражена через так называемую гипергеометрическую функцию. Радиальная часть волновой функции с учётом условия нормировки равна

Здесь F — вырожденная (конфлюэнтная) гипергеометрическая функция (функция Куммера):

которая сходится при всех конечных z ; параметр α произволен, а β предполагается не равным нулю или целому отрицательному числу. Если α есть целое отрицательное число (или нуль), то F( α , β , z ) сводится к полиному степени | α |. Радиальные волновые функции выражаются также через обобщённые полиномы Лагерра :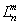

Угловая часть волновой функции описана в разделе (12.6).

В литературе можно увидеть различные формулы для волновой функции в кулоновском поле. Они отличаются друг от друга комплексной константой, квадрат модуля которой равен единице. Это различие не является существенным, так как в любом физическом эксперименте измеряется вероятность обнаружения частицы, равная именно квадрату модуля волновой функции.

Заметим, что размерность волновой функции равна см –d/2 , где d — размерность задачи. В нашем случае размерным множителем в (6.30) является комбинация ( 2k_n ) 3/2 . Остальные множители являются безразмерными, включая сферическую функцию Y_l,m.

16.7 Статистический вес энергетического уровня

Соберём воедино основные результаты, полученные в этой главе. Уровни электрона с отрицательной энергией в кулоновском поле квантуются:

,

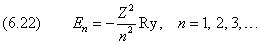
причём энергия зависит только от главного квантового числа n . Квадрат модуля момента определяется орбитальным квантовым числом l , которое при заданном уровне энергии может принимать n разных значений:

Напомним (раздел 13.5), что для краткости l часто называют абсолютной величиной момента. Существует специальная система обозначений для состояний с определённым значением l :

Решение радиального уравнения

Запишем радиальное уравнение (10.16) с кулоновским потенциалом (11.1):

+%\E+]R o (11.2)

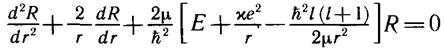
dr h2 L r 2p.r J v ‘

Для упрощения уравнения перейдем к безразмерной переменной

р=—, где а= j — постоянная, называемая боровским радиусом.

Расчет дает на основании известных констант ћ, μ, x, e следующее ее значение: а = 0,52*10 -8 см

0,5 A. Эта величина определяет порядок расстояний в атоме.

Введем также обозначения:

b& (1L3)

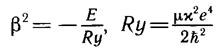
Постоянная Ry имеет размерность энергии: ее значение Ry

дает порядок энергии электрона в атоме.

Нашей целью является изучение связанных состояний электрона, для которых E 2 >0, причем β— величина безразмерная и действительная. После подстановки β и ρ в уравнение (11.2) получаем новое уравнение

Это уравнение и необходимо решить для нахождения искомой радиальной функции в поставленной выше задаче об атоме водорода.

Уравнение является дифференциальным уравнением второго порядка, причем коэффициенты при –dR/dρ и R в нем — функции ρ. Решение таких уравнений с переменными коэффициентами —довольно сложная математическая задача, разрешаемая с помощью метода степенных рядов. Приведем сначала результаты решения (ниже оно прослежено в основных чертах).

Уравнение (11.4) имеет удовлетворяющие необходимому условию квадратичной интегрируемой функции состояния решения, если выполняется равенство

где n_r= 0, 1, 2. носит название радиального квантового числа.

Обычно вводится главное квантовое число nn соотношением

откуда с учетом значений l видно, что

Из формулы (11.5) с учетом (11.6) и обозначения <5 в формуле

(11.3) следует формула энергии:

Энергия стационарных состояний квантуется главным квантовым числом n. Оно же входит и в функции стационарных состояний через радиальный множитель — решение уравнения (11.4). Мы записываем его, возвращаясь к исходной переменной r:

Здесь L — полиномы переменной величины x = 2r/na, вычисляющиеся

по полиномообразующей формуле(они называются полиномами Лагерра):

если 2r/na = х, то

Функции R_nl нормированы на единицу условием

Приведем в качестве примеров радиальные волновые функции

для основного и ближайших к нему возбужденных состояний:

рядка, причем коэффициенты при -^ и R в нем — функции р. Решение таких уравнений с переменными коэффициентами —довольно сложная математическая задача, разрешаемая с помощью метода степенных рядов. Приведем сначала результаты решения (ниже оно прослежено в основных чертах).

Уравнение (11.4) имеет удовлетворяющие необходимому условию квадратичной интегрируемой функции состояния решения, если выполняется равенство

где пг = 0, 1, 2. носит название радиального квантового числа.

Обычно вводится главное квантовое число п соотношением

откуда с учетом значений I видно, что

Из формулы (11.5) с учетом (11.6) и обозначения <5 в формуле

(11.3) следует формула энергии:

Энергия стационарных состояний квантуется главным кванто-

квантовым числом п. Оно же входит и в функции стационарных состояний

через радиальный множитель — решение уравнения (11.4). Мы

записываем его, возвращаясь к исходной переменной г:

Здесь L — полиномы переменной величины —, вычисляющиеся

по полиномообразующей формуле: если — = х, то

] (П.9)

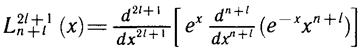
(они называются полиномами Лагерра).

Функции Rni нормированы на единицу условием

оо

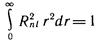
Приведем в качестве примеров радиальные волновые функции для основного и ближайших к нему возбужденных состояний:

Можно показать, что радиальные функции имеют n — l -1 узлов — пересечений с осью r в интервале (0, оо).

Проследим за принципиальными этапами решений радиального уравнения. Прежде чем искать функцию R (ρ) в виде степенного ряда, обеспечим достаточно «хорошее» поведение решения при ρ->-оо: нужно, чтобы R (ρ) стремилось к нулю.

Если ρ->-оо, то уравнение (11.4) асимптотически стремится к виду

Это асимптотическое уравнение имеет решение, обращающееся в нуль на бесконечности:

Далее оно будет принято во внимание при поисках вида решения уравнения

Надо также исключить возможную сингулярность — бесконечно большое значение R (ρ) при ρ-»0. Если ρ->0, то уравнение (11.4) может быть записано приближенно:

Это асимптотическое уравнение имеет два решения:

причем первое следует отбросить, так как R₁ -> 0 при ρ ->оо.

Итак, асимптотика решения уравнения (11.4) определяется найденными функциями. Основываясь на этом, ищем функцию R (ρ) в виде

Л(р) = е-ррр7(р). (11.13)

где f (p) — новая неизвестная функция. Подстановка предполагаемого решения

(11.13) в уравнение (11.4) приводит к следующему в нашей цепи уравнению для

неизвестной функции f (ρ):

Сделаем замену переменных в уравнении (11.14), упрощающую его:

. (11.15)

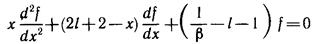
Это уравнение решаем по методу степенного ряда, т. е. ищем решение в виде

(11.16)

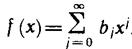
Подставляя ряд (11.16) в уравнение (11.15), имеем

Чтобы ряд (11.16) был решением уравнения (11.15), необходимо выполнение pавенства (11.17) при всех значениях х, т. е. обращение его в тождество. А последнее возможно, если сумма коэффициентов при любой степени переменной будет равна нулю.

Выпишем все слагаемые в левой части равенства (11.17), содержащие х к

(k = 0, 1, 2, . ). В первой сумме это слагаемые с j = k+1, во второй — с сомножителем

(2l+ 2) — также с j = k+1, все остальные члены берем с j = k:

Отсюда вытекает условие, которому должны удовлетворять коэффициенты

Итак, решение уравнения (11.5) найдено: это бесконечный степенной ряд, коэффициенты которого вычисляются по рекуррентной формуле (11.18), а b₀ берется произвольно н играет роль постоянной интегрирования. Но анализ показывает, что ряд (11.16) с коэффициентами (11.18) при х-»оо расходится, и притом настолько быстро, что функция R (r), задаваемая соотношением (11.13), тоже обращается в бесконечность. Поэтому решение в виде бесконечного степенного ряда не удовлетворяет физическим условиям — функция состояния электрона должна быть всюду ограниченной и затухающей на бесконечности.

Решения, удовлетворяющие требованиям ограниченности, можно получить из

бесконечного ряда: часть его (полином некоторой степени п_r) также является решением уравнения (11.4), так как его коэффициенты удовлетворяют рекуррентной формуле. Поэтому обрываем ряд на члене b_nrх nr , т. е. b_nr/=0, а все последующие коэффициенты: b_nr+1 = 0. С помощью формулы (11.18) имеем условие обрыва ряда:

где n_r = 0, 1, 2, . иосит название радиального квантового числа.

Далее, как об этом уже говорилось, формула (11.19) приводит к квантованию

энергии. Здесь же покажем; как вычисляются искомые полиномы. Рекуррентная

формула с учетом условия (11.19) приобретает внд

Здесь k — текущий индекс рассчитываемого коэффициента, а n_r — индекс (и степень) старшего члена. Задаваясь произвольным значением коэффициента b₀, для каждого n_r находим все коэффициенты b_к. Записываем полином:

Он определяется двумя параметрами: n_r н l.

Но есть и другой путь. Если подставить значение ρ, найденное из условия обрыва

ряда (11.19), выраженное через главное квантовое число

в уравнение (11.15), то получим уравнение

Оно может быть сведено к известному в математике уравнению Лагерра, а решение

его—полиномы Лагерра L 2n+1 _n+l (x)— определяется сравнительно простой в использовании для вычислений полнномообразующей формулой (11.9), приведенной выше.

Понятно, что они с точностью до постоянного множителя совпадают с ранее рассмотренным L l _nr. (Множитель значения для нас не имеет, так как функции будут

Для получения окончательного результата — решения радиального уравнения —

надо перейти к первоначальной переменной r с помощью использованных подстановок:

Отсюда с учетом формул (11.19) и (11.6)

Теперь, предусматривая в решении (11.13) исходного радиального уравнения

(11.4) нормировочный множитель N_nl, имеем окончательно

Эта формула и приведена ранее — (11.8) — с вычисленным нормировочным множителем. Радиальное уравнение решено.