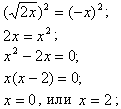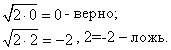Равносильные уравнения. Равносильные преобразования уравнений
Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
- Уравнения \(x+2=7\) и \(2x+1=11\) равносильны, так как каждое из них имеет единственный корень – число \(5\).
- Равносильны и уравнения \(x^2+1=0\) и \(2x^2+3=1\) — ни одно из них не имеет корней.
- А вот уравнения \(x-6=0\) и \(x^2=36\) неравносильны, поскольку первое имеет только один корень \(6\), второе имеет два корня: \(6\) и \(-6\).
Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.
Основные равносильные преобразования уравнений:
- Перенос слагаемых из одной части уравнения в другую со сменой знака слагаемого на противоположный.
Умножение или деление обеих частей уравнения на одно число или выражение не равное нулю.
Применение всех формул и свойств, которые есть в математике.
Возведение в нечетную степень обеих частей уравнения.
Извлечение корня нечетной степени из обеих частей уравнения.
Равносильные уравнения и уравнения следствия
Равносильные преобразования уравнений можно назвать «правильными» или «безошибочными» преобразованиями, потому что, сделав их, вы не нарушите математических законов. Почему тогда математики так их и не назвали: «правильные преобразования уравнений»? Потому что есть еще «полу-правильные» преобразования уравнений. В них уравнение при преобразовании приобретает дополнительные корни по ходу решения, но лишние корни мы при записи ответа не учитываем. Строгие математики их называют уравнениями следствиями:
Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
Пример (ОГЭ). Решите уравнение \(x^2-2x+\sqrt<2-x>=\sqrt<2-x>+3\)
Перенесем оба слагаемых из правой части в левую.
Взаимно уничтожим подобные слагаемые. Это и есть «полу-правильное преобразование», так как после него у уравнения становится два корня вместо изначального одного.
Это уравнение следствие из предыдущего. Найдем корни уравнения по теореме Виета .
Сверяем корни с ОДЗ и исключаем неподходящие.
\(↑\) не подходит под ОДЗ
Переходить к уравнению следствию не запрещено, но при работе с ними нужно быть осторожным и не забывать про ОДЗ .
Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.
Решение:
В пункте a) применялось равносильное преобразование 1.
В пункте b) перешли к уравнению следствию, так как \(\sqrt
В пункте с) тоже перешли к уравнению следствию, из-за того что умножили на знаменатель;
В пункте d) применялось равносильное преобразование: «Извлечения корня нечетной степени из обеих частей уравнения»;
В пункте e) умножили обе части уравнения на \(2\) т.е. равносильно преобразовали;
В пункте f) перешли от вида \(a^
Равносильные переходы в иррациональных уравнениях
Здесь вы найдете алгоритмы равносильных переходов в иррациональных уравнениях.
Напомним, что два уравнения называются равносильными (эквивалентными) , если множество всех корней первого уравнения совпадает с множеством всех корней второго уравнения.
Подробный разбор примеров смотрите здесь.
или, что тоже самое + показать
или, что тоже самое + показать
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Уравнение. Корни уравнения. Понятие о равносильных уравнениях
Уравнением называется равенство двух алгебраических выражений. В состав этих алгебраических выражений обычно входят переменные, которые называются неизвестными.
Значения неизвестных, при которых уравнение обращается в истинное равенство, называются решениями (корнями) уравнения. Решить уравнение – это значит найти все его корни.
Уравнения могут быть как с одной, так и с несколькими переменными. Например, 2x-5=3 – это уравнение с одной переменной, x=4 его единственный корень; а x-y=0 — уравнение с двумя переменными, оно имеет бесконечно много решений, например пары (1;1), (2;2), (-101,-101)… являются его решениями.
Уравнения могут не иметь решений, иметь одно решение или несколько решений, иметь бесконечно много решений. Уравнение, у которого нет корней, называется неразрешимым.
Уравнение 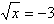
Уравнение 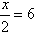
Уравнение (x-1)(x-11)x=0 имеет три решения в поле действительных чисел x=1 x=11 и x=0;
Уравнение 0*x=0 имеет бесконечно много решений в поле действительных чисел, так как любое число, умноженное на ноль, равно нулю.
Два уравнения называются равносильными, если каждое решение первого уравнения является решением второго, и наоборот – каждое решение второго уравнения является решением первого.
Уравнения (x-1)(x-11)x=0 и (2x-2)(3x-33)x=0 равносильны, так как решениями и первого, и второго уравнения являются числа 1, 11 и 0. Других решений ни у того, ни у другого уравнения нет.
Уравнения x-1=0 и x 2 -1=0 не являются равносильными, так как решениями первого уравнения является только число 1, а второго числа 1 и -1. При этом число -1 не является решением первого уравнения.
Иногда при решении уравнений исходное уравнение приходится заменять неравносильным ему уравнением, но таким, что все решения первого будут и решением второго. Особенно часто это приходится делать при решении иррациональных уравнений. Если применяется этот метод, то в конце решения обязательно нужно проверить простой подстановкой в исходное уравнение, не получилось ли лишних корней.
Решить уравнение 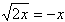
Чтобы избавиться от иррациональности, возведем обе части в квадрат, помня, что могут появиться лишние корни.
Проверим, нет ли лишних корней
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
http://egemaximum.ru/ravnosilnye-perexody-v-irracionalnyx-uravneniyax/
http://studyport.ru/raznoe/shpargalki/matematika/6835-uravnenie-korni-uravnenija-ponjatie-o-ravnosilnyh-uravnenijah