Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Практическая работа № 7 по учебной дисциплине ЕН.01 Математика
учебно-методический материал на тему
Практическая работа № 7 Решение систем линейных алгебраических уравнений
задания к работе
1 Методом Крамера найти решение системы линейных алгебраических уравнений.
2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.
3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.
4. Найти общее решение однородной системы линейных алгебраических уравнений.
В работе имеется Образец решения варианта.
Скачать:
| Вложение | Размер |
|---|---|
| prakticheskaya_rabota_7_sistemy_lineynykh_algebraicheskikh_uravneniy.doc | 443.5 КБ |
Предварительный просмотр:
Практическая работа № 7
Решение систем линейных алгебраических уравнений
Задание к работе
1. Методом Крамера найти решение системы линейных алгебраических уравнений.
2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.
3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.
4. Найти общее решение однородной системы линейных алгебраических уравнений.
Образец решения варианта.
1. Методом Крамера найти решение системы линейных алгебраических уравнений
Решение системы находим по формулам Крамера
Вычислим определитель системы
Последовательно заменив в , первый, второй и третий столбцы столбцом свободных членов, получим соответственно
2. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы
Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).
Вычислим определитель данной системы :
следовательно, система имеет единственное решение.
Данную систему можно записать в матричной форме :
, где , , .
Так как , то для матрицы существует обратная матрица . Умножив матричное уравнение слева на , получим , откуда , или .
Найдем обратную матрицу по формуле
где алгебраическое дополнение элемента .
3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений
Выпишем расширенную матрицу данной системы и приведем ее к ступенчатому виду
Последовательно умножим первую строку на (–2) и прибавим ее ко второй строке, затем умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим
Ко второй строке полученной матрицы прибавим третью строку, умноженную на , затем во вновь полученной матрице умножим третью строку на , четвертую – на (–1), затем последовательно умножим вторую строку на 2 и прибавим ее к третьей строке, умножим на 7 и прибавим к четвертой строке, получим
Третью строку полученной матрицы умножим на , четвертую – на , затем третью строку умножим на (–1) и прибавим к четвертой строке, получим
Найденная матрица имеет треугольный вид; по этой матрице запишем систему уравнений, эквивалентную исходной системе,
Последовательно находим неизвестные, начиная с последнего уравнения, ; подставим в третье уравнение найденное , вычислим , ; затем из второго уравнения находим , ; из первого уравнения получим , .
4. Найти общее решение однородной системы линейных алгебраических уравнений .
Элементарными преобразованиями строк приведем матрицу системы к эквивалентной матрице , которой соответствует уравнение , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме , или , . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе — число неизвестных и число уравнений. , матрица системы, расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра . Иногда общее решение удобнее использовать в форме
Практическая работа № 7
Решение систем линейных алгебраических уравнений
1. Методом Крамера найти решение системы линейных алгебраических уравнений.
2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.
3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.
4. Найти общее решение однородной системы линейных алгебраических уравнений
3.3 3.4
Практическая работа № 7
Решение систем линейных алгебраических уравнений
1. Методом Крамера найти решение системы линейных алгебраических уравнений.
2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.
3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.
4. Найти общее решение однородной системы линейных алгебраических уравнений
5.1 5.2
Методические рекомендации для выполнения практической работы «Системы линейных алгебраических уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Министерство образования и науки Хабаровского края
Краевое государственное бюджетное
профессиональное образовательное учреждение
«ХАБАРОВСКИЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
для выполнения практической работы
«Системы линейных алгебраических уравнений»
специальность 13.02.07 Электроснабжение (по отраслям)
Методические рекомендации учебной дисциплины ЕН.01 «Математика».
Автор рекомендаций Ивашкина Елена Сергеевна, преподаватель
Методические рекомендации для выполнения практической работы «Системы линейных алгебраических уравнений» учебной дисциплины ЕН.01 МАТЕМАТИКА рассмотрены и одобрены на заседании цикловой комиссии «Информационных систем и естественнонаучных дисциплин»
Протокол № 2 от 24.10. 2019 года.
Председатель цикловой комиссии____________ Е.В.Дерябкина
Данная работа содержит методические указания к практической работе по теме «Системы линейных алгебраических уравнений» учебной дисциплины «Математика» и предназначена для обучающихся по специальностям среднего профессионального образования.
Цель разработки: оказание помощи обучающимся в выполнении практической работы по предмету «Математика».
необходимых пояснений, полученных от преподавателя при выполнении Практические занятия служат связующим звеном между теорией и практикой. Они необходимы для закрепления теоретических знаний, полученных на уроках теоретического обучения, а так же для получения практических знаний. Практические задания выполняются студентом самостоятельно, с применением знаний и умений, полученных на уроках, а так же с использованием практического задания. К практическому занятию от студента требуется предварительная подготовка, которую он должен провести перед занятием. Список литературы и вопросы, необходимые при подготовке, студент получает перед занятием из методических рекомендаций к практическому занятию.
Практические задания разработаны в соответствии с учебной программой. В зависимости от содержания они могут выполняться студентами индивидуально или фронтально.
Зачет по каждой практической работе студент получает после её выполнения и предоставления в печатном или электронном виде, оформления отчета в котором указывает полученные знания и умения в ходе выполнения практической работы, а также ответов на вопросы преподавателя, если таковые возникнут при проверке выполненного задания.
Тема: Решение систем линейных уравнений с двумя переменными, с тремя неизвестными.
Цель: обобщить знания студентов по методам решения систем линейных уравнений с двумя переменными: графический, метод подстановки, метод алгебраического сложения, применение определителей и метода Гаусса к решению систем. Расширить, систематизировать, закрепить знания учащихся о решении систем трех линейных уравнений с тремя неизвестными.
Теоретическая часть: 1. Решение систем двух уравнений с двумя переменными методом подстановки. Метод подстановки заключается в следующем:
Одно из уравнений системы преобразуют к виду, в котором у выражено через х (или х через у).
Полученное выражение подставляют вместо у (или вместо х) во второе уравнение. В результате получается уравнение с одной переменной.
Находят корни этого уравнения.
Воспользовавшись выражением у через х (или х через у), находят соответствующее значение х (или у).
Пример. Решить систему уравнений
Решение: 1) Из первого уравнения находим выражение х через данные числа и неизвестное у:
2) Подставляем это выражение во второе уравнение:
3) Решаем полученное уравнение:
15у+48у=104-230, 63у=-126, у=-2.
Найденное значение у=-2 подставляем в выражение х =;
2. Решение систем двух уравнений с двумя неизвестными методом алгебраического сложения. Метод состоит в следующем:
1) Уравниваем модули коэффициентов при одном из неизвестных в обоих уравнениях.
2) Складываем два уравнения или вычитаем их друг из друга; этим одно из неизвестных исключается.
3) Решаем полученное уравнение с одним неизвестным.
4) Подставляем полученное значение первого неизвестного в любое из данных уравнений и находим второе неизвестное.
Пример. Решить систему уравнений
Проще всего уравнять мдули коэффициентов при у; обе части первого уравнения умножим на 2; второе уравнение остается неизменным:
3) Решаем полученное уравнение:
4) Подставляем значение х=5 в первое уравнение;
40-3у=46; -3у=46-40; -3у=6; у=-2.
3. Графическое решение систем двух уравнений с двумя переменными. Для того чтобы графически решить систему двух уравнений с двумя неизвестными, нужно в одной системе координат построить графики уравнений и найти координаты точек пересечения этих графиков.
Пример. Решить графически систему линейных уравнений
Решение:1) Выразим переменную у из первого и второго уравнений
2) Построим график уравнения у =
Также строим график уравнения у = 2х – 8
Полученные прямые не параллельны,
их пересечением является точка М(3;-2).
4. Применение определителей к решению систем двух уравнений с двумя неизвестными.
Рассмотрим систему двух линейных уравнений с двумя переменными
Вычисляем определитель системы:
a 11 , a 22 – элементы главной диагонали
a 21 , a 12 – элементы побочной диагонали
Пример: Решить систему уравнений
Примененим формулы Крамера
5. Применение формул Крамера к решению систем трех линейных уравнений с тремя неизвестными.
Система трех линейных уравнений с тремя переменными имеет вид:
Определитель третьего порядка можно вычислить методом разложения по элементам первой строки:
Формулы Крамера : ;, где
Определитель третьего порядка можно вычислить также так:
При вычислении определителя третьего порядка удобно пользоваться правилом треугольников (правило Сарруса). Это правило проиллюстрировано на схеме:
Пример: Решить систему уравнений
Решение: вычислим определители:
Итак, по формулам Крамера имеем:
6. Решение систем уравнений методом Гаусса.
Численность решений линейных алгебраических уравнений с помощью определителей удобно производить для систем 2-х и 3-х уравнений. В случае же большего числа уравнений гораздо выгоднее пользоваться методом Гаусса, который заключается в последовательном исключении неизвестных.
Метод Гаусса состоит в том, что систему уравнений приводят к эквивалентной ей треугольной системе. Это действие называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подставок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
умножение и деление коэффициентов на одно и то же число
сложение и вычитание уравнений
перестановку уравнений системы
исключение из системы уравнений, в которых все свободные члены и коэффициенты при неизвестных равны 0.
Пример: Решите систему методом Гаусса
Составим расширенную матрицу из коэффициентов при неизвестных и свободных членов
Поменяем 1-ую и 2-ую строку местами
Умножим 1-ую строку на 3, вычтем ее из 2-ой, затем, умножая 1-ую строку на 4, вычтем ее из 3-ей
Изменим знаки во 2-ой строке
Умножим 2-ую строку на 5 и сложим с 3-ей
Разделим 3-ю строку на (-11)
Используя полученную матрицу, преобразуем систему и получим решение
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2 .Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок (6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2 .Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными(6 заданий):
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2 .Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
Решить системы двух линейных уравнений с двумя неизвестными:
а) способом подстановки:
б) способом сложения:
в) графическим способом:
г) по формулам Крамера:
2. Решить системы трех линейных уравнений с тремя неизвестными:
а) по формулам Крамера:
б) методом Гаусса:
Оценка «5» ставится: работа выполнена полностью и без ошибок(6 заданий);
Оценка «4» ставится: из всех предложенных заданий не выполнено одно задание;
Оценка «3» ставится: выполнено, верно, половина из всех предложенных заданий
Оценка «2» ставится во всех остальных случаях.
[1]М.,2017 Математика, учебное пособие для техникумов,
В.Т. Лисичкин, И.Л. Соловейчик.
[2]Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных
организаций, осваивающих профессии и специальности СПО.
Краткое описание документа:
Данная работа содержит методические указания к практической работе по теме «Системы линейных алгебраических уравнений» учебной дисциплины «Математика» и предназначена для обучающихся по специальностям среднего профессионального образования.
Цель разработки: оказание помощи обучающимся в выполнении практической работы по предмету «Математика».
Практическиезанятияслужатсвязующимзвеноммеждутеориейипрактикой. Они необходимы для закрепления теоретических знаний, полученных на уроках теоретического обучения, а так же для получения практических знаний.Практические задания выполняются студентом самостоятельно, с применением знаний и умений, полученных на уроках, а так же с использованием практического задания. К практическому занятию от студента требуется предварительная подготовка, которую он должен провести перед занятием. Список литературы и вопросы, необходимые при подготовке, студент получает перед занятием из методических рекомендаций к практическому занятию.
Практические задания разработаны в соответствии с учебной программой.Взависимостиотсодержанияонимогутвыполнятьсястудентамииндивидуальноилифронтально.
Зачет по каждой практическойработестудентполучаетпосле её выполнения и предоставления в печатном или электронном виде, оформления отчета в котором указывает полученные знания и умения в ходе выполнения практической работы, а также ответов на вопросы преподавателя, если таковые возникнут при проверке выполненного задания.
http://nsportal.ru/npo-spo/estestvennye-nauki/library/2015/01/07/prakticheskaya-rabota-no-7-po-uchebnoy-distsipline-en
http://infourok.ru/metodicheskie-rekomendacii-dlya-vipolneniya-prakticheskoy-raboti-sistemi-lineynih-algebraicheskih-uravneniy-3994670.html






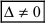 ), то система имеет единственное решение;
), то система имеет единственное решение;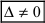 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 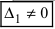 или
или 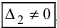 , или, . или
, или, . или 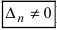 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);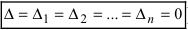 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.















