Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Метод исключения — сведение системы ДУ к одному уравнению
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.
Введением новых функций
это уравнение заменяется нормальной системой уравнений
Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка
эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения .
Проиллюстрируем этот метод на примере системы двух уравнений:
Здесь — постоянные коэффициенты, а и — заданные функции; и — искомые функции. Из первого уравнения системы (1) находим
Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение второго порядка относительно
где — постоянные. Отсюда находим . Подставив найденное выражение для и в (2), найдем .
Пример 1. Проинтегрировать систему уравнений
Решение. Из первого уравнения системы (3) находим , тогда
Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка
Общее решение уравнения (5)
Находя производную по от (6), получаем
Общее решение системы (3):
Пример 2. Решить задачу Коши для системы
Решение. Из второго уравнения системы (7) находим
Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение , общее решение которого
Подставляя (11) в (9), найдем . Общее решение системы (7)
При начальных условиях (8) из (12) получим систему уравнений для определения
решая которую, найдем . Подставляя эти значения и в (12), получаем решение поставленной задачи Коши:
Пример 3. Решить систему уравнений
Решение. Из первого уравнения системы находим
Подставляя эти выражения для и во второе уравнение, получаем
Считая , из последнего уравнения имеем и после интегрирования получим . Теперь легко находим
Общее решение данной системы
Замечание. Не всякая система дифференциальных уравнений может быть сведена к одному уравнению более высокого порядка. Например,
не сводится к одному уравнению второго порядка. Ее общее решение .
Решение систем линейных алгебраических уравнений методом исключения Гаусса
Решение систем линейных алгебраических уравнений
методом исключения Гаусса
Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

или в матричной форме 
Найдем решение СЛАУ (1) методом исключения Гаусса.
Прямой ход метода Гаусса.
Пусть 


Преобразуем СЛАУ (1) следующим образом: 1-е уравнение оставим без изменения; из 2-го уравнения вычтем уравнение (2), умноженное на 



Назовем элемент 


или 
Обратный ход метода Гаусса
СЛАУ (4) легко решается, начиная с последнего уравнения.

или 

Нахождение решения по формулам (5) называется обратным ходом метода Гаусса.
Метод Гаусса и его модификации является одним из наиболее эффективных методов решения СЛАУ.
Пример: решить СЛАУ
Составим расширенную матрицу
Получим эквивалентную СЛАУ


Переход от (a) к (b) завершает прямой ход метода Гаусса. Обратный ход:
Ответ:
1. Если в процессе прямого хода ведущий элемент окажется равным нулю, то следует поменять уравнения местами так, чтобы на главной диагонали в качестве ведущего оказался ненулевой элемент. Если окажется, что диагональный и все стоящие в столбце ниже него элементы равны нулю, то это означает, что данная СЛАУ является вырожденной (определитель матрицы коэффициентов при неизвестных равен нулю). Вырожденная СЛАУ либо не имеет решения, либо имеет их бесконечное множество.
2. Если ведущий элемент мал, то деление на него приводит к большим ошибкам округления. Этого позволяет избежать метод Гаусса с выбором главного элемента по столбцам (или по строкам, или по всей матрице).
При выборе главного элемента по столбцам строки расширенной матрицы переставляются так, чтобы на главной диагонали (то есть в качестве ведущего) оказался наибольший из элементов 

3. Общее число операций при решении СЛАУ методом Гаусса пропорционально 

Вычисление определителя методом Гаусса
При выполнении операций прямого хода метода Гаусса величина определителя матрицы A не меняется. При каждой перестановке строк или столбцов матрицы знак определителя меняется на противоположный. Таким образам,

где U – верхняя треугольная матрица, которая получается из матрицы коэффициентов A в результате выполнения прямого хода метода Гаусса; k – суммарное число перестановок строк и столбцов в процессе выполнения прямого хода.
Нахождение обратной матрицы методом Гаусса-Жордана
В методе Жордана при решении СЛАУ исключаются как элементы, стоящие ниже ведущего, так и элементы, стоящие выше ведущего в данном столбце матрицы А коэффициентов при неизвестных. Кроме того, все элементы строки матрицы, содержащей ведущий элемент, делятся на него. При этом после выполнения прямого хода матрица А приводится к единичной матрице и обратный ход становится не нужным. Решение СЛАУ получается в расширенной матрице на месте свободных членов. Однако, при решении СЛАУ метод Жордона несколько медленнее метода Гаусса. Но он быстрее метода Гаусса при нахождении обратной матрицы.
Пусть дана матрица А и нужно найти обратную к ней. Имеем

Соотношение (*) фактически представляет собой совокупность n СЛАУ с одной и той же матрицей А коэффициентов при неизвестных, где в качестве неизвестных берутся элементы столбцов обратной матрицы 

Составим расширенную матрицу и выполним прямой ход методом Жордана. Умножим первую строку расширенной матрицы на (-2) и сложим со второй строкой. Затем умножим первую строку на (1) и сложим с третьей строкой. После этого разделим все элементы первой строки на (2). Получим

Теперь умножим вторую строку полученной матрицы на (0.5) и сложим с первой строкой. Затем умножим вторую строку на (3) и сложим с третьей строкой. После этого разделим все элементы второй строки на (-1). Получим

Наконец, умножим третью строку полученной матрицы на (-0.125) и сложим с первой строкой. Затем умножим третью строку на (0.5) и сложим со второй строкой. После этого разделим все элементы третьей строки на (-4). Получим

Обратная матрица получается в расширенной матрице на месте единичной матрицы.

Замечание. Если известна обратная матрица 


http://mathhelpplanet.com/static.php?p=metod-isklyucheniya
http://pandia.ru/text/78/393/68657.php






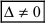 ), то система имеет единственное решение;
), то система имеет единственное решение;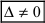 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 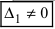 или
или 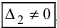 , или, . или
, или, . или 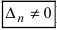 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);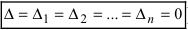 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.



















