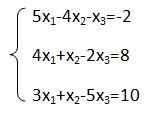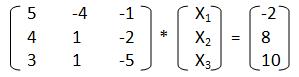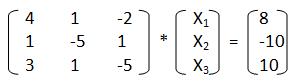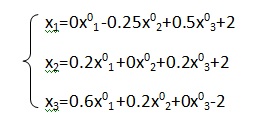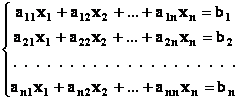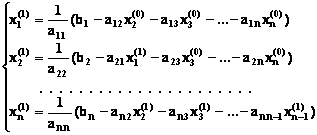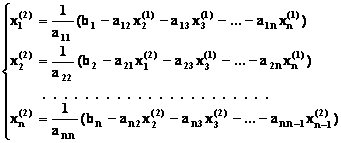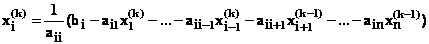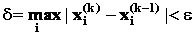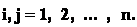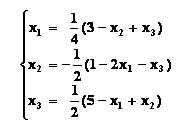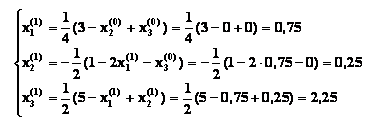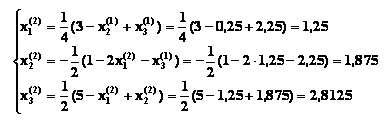Итерационные методы решения СЛАУ. Метод простых итераций. Метод Зейделя.
Введение
Методы решения систем линейных алгебраических уравнений классифицируют на прямые (точные) и итерационные. Прямые методы основаны на выполнении конечного числа арифметических операций, это, например, метод обратной матрицы, метод Гаусса, метод Гаусса-Жордана, метод прогонки для трехдиагональных матриц и т.д. Суть итерационных методов, в свою очередь, заключаются в том, чтобы за счет последовательных приближений получить решение системы, определяемое необходимой точностью. Я попытаюсь наиболее подробно рассмотреть два из них, а именно метод простых итераций и метод Зейделя. Они практически эквивалентны, поэтому ограничусь подробным анализом метода простых итераций, а в конце пару слов скажу по поводу метода Зейделя. А прежде чем приступить к рассмотрению какого-то конкретного метода, хочется немного описать итерационные методы решения СЛАУ в общем плане.
Эти методы характеризуются большими расчетными объемами, что не мешает им быть по своей структуре достаточно простыми. Всего-навсего за счет предыдущих приближений мы получаем новые приближения, и, если система удовлетворяет условию сходимости, то эти приближения все меньше и меньше отличаются от аналитического решения.
Для итерационных методов можно выделить три последовательных этапа:
- Приведение исходной системы вида
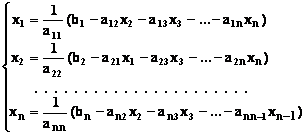
к итерационной форме
.
- Проверка условия сходимости.
- Решение системы одним из методов.
Метод простых итераций
Теперь, опираясь на представленную последовательность, разберем метод простых итераций. Сразу условимся, что для общего вида систем выполняется тождество m=n, где m — количество уравнений в системе, n — количество неизвестных. Т.е. не имеет смысла решать недоопределенные (m n) системы, т.к. они могут быть сведены путем элементарных алгебраических преобразований к нормальным (m=n) системам линейных уравнений. Другими словами, если у вас имеется «ненормальная» система, то прежде, чем использовать метод простых итераций, преобразуйте ее к нормальной.
Все мы знаем, что система линейных уравнений может быть записана в матричной форме, где A – матрица коэффициентов, b – вектор свободных членов, x – вектор неизвестных. Возьмем систему:
Ее матричная форма:
Смотрим на первый этап итерационных методов – он предполагает преобразование исходной системы, а именно матрицы А и вектора b к итерационной форме, где С и d – итерационные формы исходных данных.
Переход к итерационному виду осуществляется по следующим формулам:
Также следует отметить, что, несмотря на эти формулы, диагональные элементы новой матрицы обнуляются, хотя должны быть равны -1.
В итоге для нашей системы должно получиться:
Проверьте. Ошибка? Если считать по исходной системе, то да. Все дело в том, что я не сказал про одно «НО».
Это «НО» заключается в следующем. Если мы будем преобразовывать исходную систему к итерационной форме, то она не удовлетворит условию сходимости:
Некоторые элементы матрицы C будут больше единицы. А глядя на условие сходимости, становится понятно, что, если хотя бы один будет больше единицы, то условие не выполнится, и решение системы путем простых итераций не будет найдено.
Поэтому открываем учебник по линейной алгебре и вспоминаем элементарные матричные преобразования! Прежде чем следовать этапам итерационных методов, нужно привести исходную систему к виду, в котором все диагональные элементы были бы максимальными по модулю в своих строках. Только при таком виде матрицы коэффициентов можно надеется на выполнение условия сходимости.
Смотрим нашу начальную систему. Видим, что третий элемент третьей строки по модулю больше других. Оставим его неизменным. Меняем местами первую и вторую строки. Теперь умножаем строку, ставшую первой, на -1 и складываем с новой второй. В итоге получаем:
Теперь при подстановке в формулы мы получим итерационную форму верно. К сожалению, это преобразование начальной системы к «благоприятному» виду — чистая аналитика, поэтому записать его в программный код очень сложно, а если даже и попытаться, то в некоторых случаях вероятно возникновение ошибок.
Переходим ко второму этапу: «Проверка условия сходимости» (формулу смотрите выше). Если система не проходит проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. В этом случае можно попытаться получить другую «благоприятную» форму. Если условие сходимости выполнено, то стратегия метода простых итераций применима и осуществляется переход к третьему этапу.
В конечном счете, мы получили систему линейных алгебраических уравнений в итерационной форме:
где x1, x2, x3 – приближения, получаемые на текущей итерации за счет приближений полученных на предыдущей итерации — x 0 1, x 0 2, x 0 3.
Итерационный процесс в методе простых итераций идет до тех пор, пока вектор приближений не достигнет заданной точности, т.е. пока не выполнится условие выхода:
Я думаю, что теории достаточно, осталось лишь обратить внимание на программную реализацию метода.
Далее представлен код, написанный в среде PascalABC.Net. Эта система была выбрана мной благодаря возможности работать с динамическими массивами (в Turbo Pascal предусмотрены только статические). Поэтому программа может решать любую нормальную систему линейных уравнений, которая проходит проверку условия сходимости. Главное, чтобы вид этой системы соответствовал вышеописанным критериям.
Применимо к нашей СЛАУ программа выдаст ответ: x1=1.0000002, x2=2.000000009, x3=-1.0000002. Такой вектор приближений соответствует точности 10 -6 , прописанной в коде.
Метод Зейделя
Как я уже говорил, метод простых итераций и метод Зейделя почти идентичны. Разница лишь в том, что в методе Зейделя расчет вектора приближений на текущей итерации происходит с использованием данных, полученных ни только на предыдущей, но и на нынешней итерации. То есть элемент x1 вычисляется на основе x2 и x3, значения которых, расчитаны на предыдущей итерации, а следующий элемент x2 уже вычисляется за счет x1, полученного именно на текущей итерации, и x3 на предыдущей. Другими словами данные в методе Зейделя для расчета вектора X поступают в процесс по мере их вычисления. А в методе простых итераций используются данные, строго полученные на предыдущей итерации.
Это различие говорит нам о том, что метод Зейделя обладает наилучшей сходимостью нежели метод простых итераций, так как для него характерна тенденция использования приближений, получаемых по ходу процесса, наиболее близких к конечному результату.
И на последок покажем это различие в практической реализации. Чтобы метод простых итераций «превратился» в метод Зейделя нужно поменять процедуру ProstIterMetode, например, на следующую:
Решение систем линейных уравнений методом зейделя паскаль
2 . Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений (СЛАУ) широко используются во многих областях прикладной математики. Оставляя за рамками данной работы вопросы теории линейных систем, отметим, что некоторые СЛАУ могут вообще не иметь решения или иметь бесконечное множество решений. В дальнейшем мы будем рассматривать только системы, имеющие единственное решение.
В общем виде система из n уравнений с n неизвестными выглядит так:
Таким образом, даны квадратная матрица коэффициентов при неизвестных < aij >, i , j = 1, 2, … , n , и вектор-столбец свободных членов (правых частей уравнений) < bi >, i = 1, 2, … , n . В результате решения требуется определить n неизвестных x 1 , x 2 , … , xn , которые удовлетворяют одновременно всем уравнениям системы.
Все методы решения СЛАУ делятся на две группы – прямые и итерационные. Прямые методы дают решение после выполнения конечного числа операций. Эти методы достаточно универсальны, но в ряде случаев полученное решение не является достаточно точным. Итерационные методы используют последовательные приближения (итерации) к искомому результату. Они позволяют получить решение с любой заданной точностью, но при их использовании заранее неизвестно количество предстоящих итераций, более того, итерационные методы в некоторых случаях вообще не дают решения.
В данном пособии мы рассмотрим по одному методу из каждой группы.
Метод Гаусса
Суть метода состоит в следующем. Вначале квадратную матрицу коэффициентов при неизвестных преобразуют в верхне-треугольную матрицу (прямой ход). Для этого сначала первое неизвестное исключают из второго и последующих уравнений системы, затем второе неизвестное исключают из третьего и последующих уравнений и так далее. Таким образом, в последнем уравнении остается только одно неизвестное. Для реализации прямого хода используют следующие известные правила:
— любое уравнение системы можно умножить на постоянный коэффициент;
— можно сложить два любых уравнения системы и результат записать вместо одного из этих уравнений.
На втором этапе последовательно вычисляют значения всех неизвестных, начиная с последнего (обратный ход).
Рассмотрим применение метода Гаусса на примере. Пусть имеем такую систему из трех уравнений:
Для исключения первого неизвестного из второго уравнения умножим первое уравнение на ( — a 21 / a 11 ), т.е. на –0,5. Первое уравнение примет вид
Сложив его со вторым уравнением исходной системы (2.2), получим
Можно заметить, что неизвестное x 1 в данном уравнении отсутствует.
Для исключения первого неизвестного из третьего уравнения системы (2.2) умножим первое уравнение этой системы на ( — a 31 / a 11 ), т.е. на –0,25. Первое уравнение примет вид
Сложив его с третьим уравнением исходной системы (2.2), получим
Можно заметить, что и в этом уравнении неизвестное x 1 отсутствует.
Таким образом, система (2.2) примет вид
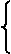
Теперь исключим неизвестное x2 из третьего уравнения системы (2.3), сложив его со вторым уравнением системы (2.3), умноженным на –0,5. Получим систему
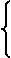
Прямой ход закончен, исходная матрица коэффициентов приведена к верхне-треугольному виду. В третьем уравнении системы (2.4) присутствует только неизвестное x 3 . Теперь легко осуществить обратный ход, т.е. вычислить неизвестные. Из третьего уравнения вычислим x 3 , далее его значение подставим во второе уравнение и вычислим x 2 , а затем из первого уравнения найдём x 1 . Получим ответ: x 1 = 1; x 2 = 2; x 3 = 3. Задача решена.
Программа для решения СЛАУ методом Гаусса может иметь такой вид:
var a:array [1..n,1..n] of real;
b, x : array [1..n] of real;
i, j,k : integer; c,s : real;
for i :=1 to n do
writeln (‘Введите коэффициенты уравнения’, i );
for j:=1 to n do read (a[ i,j ]);
writeln (‘Введите свободный член уравнения’, i );
for k:=1 to n-1 do
for i :=k+1 to n do
for j:= k+1 to n do a[ i,j ]:=a[ i,j ]+c*a[ k,j ];
for i :=n-1 downto 1 do
for j:=i+1 to n do s:= s+a [ i,j ]*x[j];
writeln (‘ Решение системы ’);
for i :=1 to n do write (x[ i ]:8:4);
Данный метод является одним из самых распространенных итерационных методов решения СЛАУ, поскольку он отличается простотой и легкостью программирования. Рассмотрим его суть. Допустим, диагональные коэффициенты исходной матрицы < aij >отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему (2.1) в следующем виде:
Если теперь задать для неизвестных их начальные приближенные значения 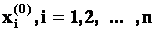
Используя найденные значения неизвестных , можно еще более уточнить их на второй итерации:
В данном методе для нахождения значения i -го неизвестного на каждой итерации используются значения предыдущих неизвестных, уже найденные на данной итерации. Общую формулу определения i -го неизвестного на k — й итерации для системы n уравнений можно записать так:
Итерационный процесс продолжается до тех пор, пока все значения xi ( k ) , не станут достаточно близкими к xi ( k -1) . Близость этих значений можно охарактеризовать максимальной абсолютной величиной их разности d . Тогда при заданной точности вычислений e > 0 критерий окончания итерационного процесса можно записать в виде:
При выполнении этого условия итерационный процесс называется сходящимся. В этом случае максимальные разности между значениями соответствующих неизвестных в двух последовательных итерациях убывают, а сами значения стремятся к решению системы.
Доказано, что для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения были не меньше суммы модулей всех остальных коэффициентов:
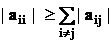
При этом хотя бы для одного уравнения неравенство (2.10) должно выполняться строго.
В качестве примера рассмотрим решение методом Гаусса-Зейделя системы (2.2). Заметим, что достаточное условие сходимости итерационного процесса (2.10) для этой системы соблюдается. Запишем исходную систему в виде:
В качестве начальных приближений возьмем нули, т.е. примем x 2 (0) = x 3 (0) = 0.
Найдем значения неизвестных на первой итерации:
Далее произведем вторую итерацию:
Производя аналогично третью и последующие итерации, найдем:
Нетрудно заметить, что разности между значениями соответствующих неизвестных в процессе итераций убывают, следовательно, процесс решения сходящийся, что и следовало ожидать. Если принять точность вычислений e = 0,02 , то итерации следует закончить. При увеличении заданной точности вычисления корней, число итераций возрастает, например, при e = 0,00001 следует выполнить 11 итераций, а результат будет x 1 (11) = 1,000000; x 2 (11) = 1,999998; x 3 (11) = 2,999999.
Программа для решения СЛАУ методом Гаусса-Зейделя приведена ниже. Поскольку при некорректной постановке задачи количество итераций может стать излишне большим, в программе предусмотрено прекращение итерационного процесса при превышении заранее заданного предельного числа итераций.
var a:array [1..n,1..n] of real;
b, x:array [1..n] of real;
for i :=1 to n do
writeln (‘Введите коэффициенты уравнения’, i );
for j:=1 to n do read (a[ i,j ]);
writeln (‘Введите свободный член уравнения’, i );
writeln (‘ Введите точность ‘); readln (e);
writeln (‘Введите допустимое кол-во итераций’); readln ( m );
Дипломная работа на тему «Метод Зейделя»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных)задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.
Одна из трудностей практического решения систем большой размерности связанна сограниченностью оперативной памяти ЭВМ. Хотя объем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритм о в линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памяти ЭВМ.
К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств – сложные строительные конструкции и большие электрические цепи.
Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы невозможно, если бы соответствующие матрицы не являлись разреженными (матрица системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75 Гбайт).
1 .Глава. Модификация метода простых итераций
Модификацией метода простых итераций Якоби можно считать метод Зейделя.
В методе Якоби на (k+1)-ой итерации значения x








x 





x 




x 




x 




Формулы (3.36) являются расчетными формулами метода Зейделя.
Введем нижнюю и верхнюю треугольные матрицы:
0 
b21 0 0 … 0 0 0 b23 … b2n
B 1 = b31 b32 0 … 0 и B 2 = 0 0 0 … b3n .
bn1 bn2 bn3 …0 0 0 0 … 0
Матричная запись расчетных формул (3.36) имеет вид:
так как B = B1+ B2, точное решение x* исходной системы удовлетворяет равенству:
http://dit.isuct.ru/IVT/sitanov/Literatura/M866/Glava2.htm
http://infourok.ru/diplomnaya-rabota-na-temu-metod-zeydelya-398217.html
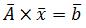 к итерационной форме
к итерационной форме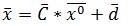 .
.