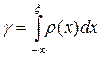Решение систем линейных уравнений монте карло

VMath

Инструменты сайта

Основное

Информация

Действия

Вспомогательная страница к разделу СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Для понимания материалов этого пункта полезно ознакомиться с идеологией метода Монте-Карло

Решение системы линейных уравнений методом Монте-Карло

Рассмотрим систему из $ n_<> $ линейных уравнений относительно $ n_<> $ неизвестных $$ \left\< \begin a_<11>x_1 &+a_<12>x_2&+ \ldots&+a_<1n>x_n &=b_1,\\ a_<21>x_1 &+a_<22>x_2&+ \ldots&+a_<2n>x_n &=b_2,\\ \dots & & & & \dots \\ a_x_1 &+a_x_2&+ \ldots&+a_x_n &=b_n, \end \right. $$ которую иногда будем представлять и в матричном виде $$ AX= \mathcal B \ . $$ Решение этой системы равносильно нахождению минимума квадратичной функции $$ F(X)=\sum_^n \alpha_j \left(a_x_1+\dots+a_x_n-b_j \right)^2= (AX-\mathcal B)^ <\top>\left( \begin \alpha_1 & 0 & \dots & 0 \\ 0 & \alpha_2 & \dots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \dots & \alpha_n \end \right) (AX-\mathcal B) \ , $$ где $ \< \alpha_j\>_^n $ — положительные числа, а $ <>^ <\top>$ означает транспонирование.

Если исходная система линейных уравнений имеет единственное решение $ X=X_<\ast>=(x_<1\ast>,\dots, x_) $, то в пространстве $ \mathbb R^ $ уравнение $$ F(X) = 1 $$ задает эллипсоид с центром в точке $ X_ <\ast>$. Каждая из $ (n_<>-1) $-мерных гиперплоскостей $ x_k=x_ $ ( линейных многообразий), проходящих через центр эллипсоида, делит его объем пополам.

Построим $ n_<> $-мерный параллелепипед $$ A_1 ☞ ЗДЕСЬ: $$ V_ <\mathrm E>\approx 3133.207748 \ . $$ $$ \begin N & 1000 & 5000 & 10000 & 20000 & 50000 \\ \hline M & 62 & 297 & 581 & 1181 & 2885 \\ \hline V_ <\Pi>M/N & 3339.6300 & 3199.581 & 3129.5565 & 3180.7282 & 3108.0105 \\ \hline \overline <\xi_1>& 3.2592 & 3.2745 & 3.1230 & 3.1020 & 3.1798 \\ \hline \overline <\xi_2>& 0.9406 & 1.5346 & 1.4669 & 1.4867 & 1.5141 \\ \hline \overline <\xi_3>& 0.3453 & 0.5163 & 0.3996 & 0.5001 & 0.4299 \\ \hline \overline <\xi_4>& -1.7029 & -2.2198 & -2.1676 & -2.1545 & -2.2413\\ \end $$ Решение системы $$ x_1=\frac<257> <84>\approx 3.05952,\ x_2=\frac<53> <36>\approx 1.47222,\ x_3=\frac<55> <126>\approx 0.43651 , x_4=-\frac<547> <252>\approx -2.17063 \ . $$

Источник

Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний Монте-Карло и его реализация в цифровых машинах. М.: Физматгиз, 1961. 266 с.

Решение линейных алгебраических систем методом Монте-Карло

Существует множество методов решения линейных алгебраических систем методом статистических испытаний[2]. Рассмотрим метод применимый к решению системы линейных алгебраических уравнений общего вида

, (9)

Решение системы (9) равносильно минимизации квадратичной формы:

, (10)

Учитывая (10), определим n-мерный эллипсоид

. (11)

Пусть — вектор решения системы уравнений (9), тогда очевидно, что вектор является центром симметрии эллипсоида (11). Это означает, что каждая из гиперплоскостей , проходящая через центр эллипсоида, делит его объем пополам. По этой причине решение системы (9) сводится к нахождению таких значений , что объемы частей эллипсоида, лежащих в полупространствах и совпадают и равняются половине объема эллипсоида (11).

Из данных соображений вытекает следующий способ решения. Возьмем n-мерный параллелепипед

в который заведомо помещается n-мерный эллипсоид.

Рассмотрим статистическую серию из N векторов

, (12)

где k = 1,2,…,N и случайная компонента равномерно распределена на отрезке [A_i,B_i], i = 1,…,n.

Отберем среди набора векторов (12) те, которые попадают в эллипсоид (11), т.е. удовлетворяют условию . Пусть таких векторов оказалось M. Рассмотрим среднее арифметическое векторов, попавших в эллипсоид, тогда можно записать следующее представление:

, (13)

из которого следует способ нахождения вектора решений исходной системы уравнений (9).

Можно оценить дисперсию случайной величины (13). Она равна

где V¢ — n-мерный объем, удовлетворяющий неравенству .

На листинге_№6 приведен код программы, которая решает систему уравнений (9) методом Монте-Карло согласно алгоритму (13).

%Задача решения линейной алгебраической системы

%уравнений ax=b методом Монте-Карло

%Определяем размерность системы уравнений (9)

%Определяем вектор решений x0 системы уравнений (9)

%В качестве матрицы a выбираем случайную матрицу,

%а правую часть b находим из уравнения b=ax0

%Определяем параллелепипед, в который помещается

%Оцениваем константу С, входящую в определение

%Организуем цикл расчетов с разными длинами

%статистических серий N

%решения x к точному решению x0

%Рисуем зависимость относительной ошибки от длины

%статистической серии N

%Определяем квадратичную форму (10)

На рис.6 приведен итог работы кода программы листинга_№6. На фигуре изображена кривая, изображающая динамику относительной ошибки error = ||x — x₀||/||x₀||, где x — численное решение системы уравнений (9), а x₀ — точное решение системы уравнений (9).

Рис.6. Решение линейной системы уравнений (9) методом
Монте-Карло

Вычисление интегралов

Значение случайной функции f(x) заключено между f(x) и f(x + dx), если случайная величина x заключена между x и x + dx. Вероятность такого события равна r(x)dx. В этом случае математическое ожидание и дисперсия случайной функции можно оценить согласно формулам:

, (14)

. (15)

Первый способ вычисления интегралов с помощью метода Монте-Карло базируется на формуле (14), т.е. одномерный интеграл можно рассматривать как математическое ожидание случайной функции f(x), аргумент которой является случайной величиной с плотностью распределения r(x).

Математическое ожидание можно приближенно вычислить, исходя из центральной предельной теоремы теории вероятностей. Если h является случайной величиной, то среднее арифметическое N испытаний

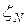
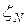
также является случайной величиной с тем же математическим ожиданием, т.е. , при это распределение случайной величины стремится к нормальному распределению с дисперсией при N ® ¥. Таким образом, при большом числе испытаний дисперсия будет малой величиной, а значение средней арифметической с вероятностью близкой к единице будет близко к математическому ожиданию. Учитывая эти соображения, можно положить

, (16)

где x — случайная величина с плотностью распределения r(x).

Оценим дисперсию (15), заменяя в ней математические ожидания на соответствующие суммы типа (16), тогда

. (17)

Делитель N — 1 вместо N в (17) связан с тем соображением, что для оценки выборочной дисперсии используется так называемая несмещенная оценка. Впрочем, это существенно лишь при малой длине выборки N.

При статистических испытаниях численные оценки тех или иных величин носят вероятностный характер, т.е. они в принципе могут как угодно сильно отличаться от точного значения. Однако, согласно свойствам нормального распределения, с вероятностью 99,7% ошибка не превосходит три стандартных отклонения, т.е. величины . При увеличении числа статистических испытаний N ошибка ответа будет уменьшаться, примерно, как . Отметим, что зависимость относится не к самой ошибке, а к тем доверительным интервалам, в которые ошибка попадает с заданной вероятностью.

В качестве примера найдем методом статистических испытаний интеграл

, (18)

значение которого равно нулю. Применим к интегралу формулы (15), (16), тогда получим следующие расчетные формулы

, (19)

, (20)

где x — случайная величина с плотностью , — выборочная дисперсия. Случайную величину x для решения задачи (18) — (20) разыграем согласно формуле (7), где g — равномерно распределенная на отрезке [0,1] случайная величина, генерируемая с помощью генератора псевдослучайных чисел (5) с параметрами A = 5 13 и g₀ = 2 — 36 .

На листинге_№7 приведен код программы взятия интеграла (18) методом Монте-Карло по формулам (19), (20).

%Пример взятия интеграла (18) методом статистических

%испытаний согласно формулам (19), (20)

%Задаем число удвоений числа статистических испытаний

%Задаем значения констант A и gamma0 для генерации

%согласно алгоритму (5) псевдослучайных чисел,

%распределенных равномерно на отрезке [0,1]

%Организуем цикл расчетов с различным числом

%статистических испытаний N

%Генерируем последовательность псевдослучайных

%чисел gamma, согласно алгоритму (5), а также

%случайные числа xi с плотностью 0.5*exp(-abs(x))

gamma=gamma0; I(n)=0; s=0;

%Вычисляем искомый интеграл I и соответствующую

%дисперсию delta согласно формулам (19), (20)

%Вычисляем доверительный интервал con_int с

%Определяем массив с числом испытаний в каждом

%Рисуем сходимость численного значения интеграла (18)

%в зависимости от числа испытаний N в отдельном

%Рисуем зависимость длины доверительного интервала с

%99,7% надежностью от числа испытаний N в отдельном

На рис.7 приведен итог работы кода программы листинга_№7. На левом рисунке приведена зависимость абсолютного значения искомого интеграла от числа испытаний в статистическом эксперименте (все координаты выбраны логарифмическими). Видна сходимость в среднем численной оценки к искомому значению интеграла, равному нулю. На правом рисунке приведена зависимость границы доверительного интервала с надежностью 99,7% от числа испытаний в статистическом эксперименте. Согласно определению доверительного интервала, введенному в выборочном методе статистики, искомое значение интеграла I с вероятностью » 99,7% находится в интервале

Рис.7. Численное взятие интеграла (18) методом Монте-Карло

Второй метод взятия интеграла методом статистических испытаний применяется к интегралам вида , при этом считается, что 0 £ f(x) £ 1, x Î [0,1]. Произвольный интеграл можно привести к такому виду некоторой линейной заменой переменных.

Пусть имеется набор из N пар <(g₁,g₂),(g₃,g₄),…,(g₂_N_—₁,g₂_N)>, равномерно распределенных на единичном отрезке случайных чисел. Рассмотрим пары чисел как координаты точек единичного квадрата координатной плоскости x и y (левый график на рис.8).

Поскольку точки на плоскости распределены случайно и равномерно в единичном квадрате, постольку вероятность попадания точки под кривую y = f(x) равна площади, заключенной под кривой, т.е. искомому интегралу I = . Условие попадания точки под кривую определяется неравенством . Доля точек из всего набора N точек, которая удовлетворяет данному неравенству, дает приближенное значение искомого интеграла.

Рис.8. Взятие интеграла 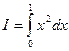методом статистических испытаний

На листинге_№8 приведен код программы численного взятия интеграла методом статистических испытаний.

%Пример взятия интеграла от функции y=x^2 вторым

%способом в методе статистических испытаний

%Создаем массив точек на плоскости (x,y) со

%случайными, равномерно распределенными на

%единичном отрезке числами

%Определяем подынтегральную функции yi=xi^2

%Рисуем массив случайных точек и

%Определяем число удвоений числа точек на

%плоскости, координаты которых равномерно

%распределены на единичном отрезке

%Организуем цикл расчетов искомого интеграла

%для различного количества случайных точек на

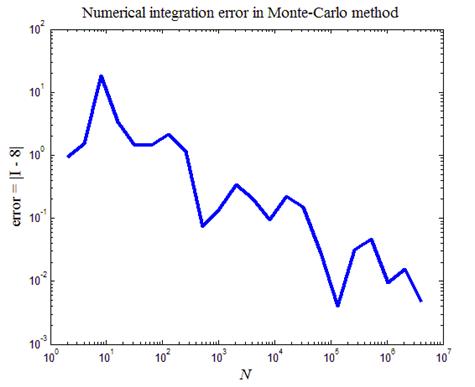
if y(i) 2 , а также N = 1000 случайных точек в единичном квадрате. Подсчитывалась доля точек, которые оказывались ниже кривой y = x 2 . На правом рисунке изображена зависимость ошибки численного интегрирования error = |I — 1/3| от параметра N — числа точек в статистической серии. Видно, что в среднем, по мере роста параметра N, ошибка численного интегрирования стремится к нулю.

Оптимизация дисперсии. Точность взятия интеграла методом Монте-Карло можно повысить, подбирая специальным образом случайную величину. Пусть g(x) = f(x)r(x), тогда исходный интеграл запишется в виде: , где функция r(x) нормирована таким образом, что ее можно считать плотностью распределения некоторой случайной величины. Задача состоит в том, чтобы, путем подбора плотности распределения r(x), добиться минимума дисперсии (15).

В дисперсии отдельного испытания (15) второе слагаемое , оно не зависит от плотности r(x), поэтому условие минимума сводится к условию:

Добавляя условие нормировки плотности r(x), получим следующую задачу оптимизации:

Находя вариационные производные и приравнивая их нулю, получим

Для равенства вариационных производных нулю необходимо и достаточно, чтобы , т.е. . В этом случае дисперсия не просто минимальна, а равна нулю, когда g(x) знакопостоянна.

На практике взять не удается, т.к. для моделирования случайной величины с такой плотностью необходимо решить уравнение

которое равносильно по сложности исходной задаче взятия интеграла I. По этой причине плотность r(x) подбирают так, чтобы уравнение

относительно x решалось просто, а сама плотность r(x) была как можно ближе к g(x).

Смысл увеличения точности состоит в том, что, если r(x)

|g(x)|, то f(x) почти постоянна и все испытания дают близкие результаты.

В качестве примера рассмотрим взятие интеграла

» 0.13940279264033. (21)

Будем считать, что 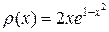, при этом . Случайную величину с такой плотностью разыгрываем согласно формуле

Откуда следует, что

, (22)

. (23)

На листинге_№9 приведен код программы взятия интеграла (21) с помощью алгоритма статистических испытаний с уменьшенной дисперсией, т.е. с помощью вычислительных формул (22), (23).

%Взятие интеграла (21) методом Монте-Карло

%с уменьшенной дисперсией по формулам (22), (23)

%Определяем число удвоений количества чисел

%в статистической серии

%Организуем цикл расчетов с различными

%длинами статистических серий

%Определяем искомый интеграл (21) согласно

%вычислительной формуле (23)

%Определяем дисперсию численной оценки

%Определяем ошибку численной оценки

%Определяем границу доверительного интервала

%с надежностью 99,7%

%Рисуем зависимость ошибки численной оценки

%интеграла от количества испытаний N в

%Рисуем зависимость границы 99,7% надежности от

%количества испытаний N в статистической серии

На рис.9 приведен итог работы кода программы листинга_№9. На левом рисунке приведена зависимость ошибки численного интегрирования от длины статистической серии. По сравнению с предыдущим примером точность заметно повысилась. На правом рисунке приведена зависимость границы доверительного интервала с 99,7% надежностью от длины статистической серии. Этот график заметно отличается от аналогичного графика, представленного на рис.7. При одной и той же длине статистической серии N границы доверительного интервала значительно уже в данном случае, чем в том примере, который приведен на рис.7 и где процедура оптимизации дисперсии не проводилась.

Рис.9. Взятие интеграла (20) методом статистических испытаний с
уменьшенной дисперсией

Многомерные интегралы. Второй способ легко обобщается на многомерные интегралы по единичному кубу G, если значения подынтегральной функции лежат в единичном интервале.

Рассмотрим для определенности трехмерное пространство с координатами x, y, z и интеграл вида

. (24)

Интеграл (24) легко берется путем его факторизации и взятием трех одномерных интегралов.

Пусть определена совокупность N четверок (g₁,g₂,g₃,g₄), (g₅,g₆,g₇,g₈), …, (g₄_N_—₃,g₄_N_—₂,g₄_N_—₁,g₄_N), равномерно распределенных на единичном интервале случайных чисел. Каждая из четверток определяет случайную точку в единичном четырехмерном кубе . Доля случайных точек, удовлетворяющих неравенству , где определяет приближенное значение искомого интеграла.

На листинге_№10 приведен код программы взятия интеграла (24) вторым способом в методе статистических испытаний.

%Численное интегрирование вторым способом в

%методе статистических испытаний на примере

%взятия многомерного интеграла (24)

%Определяем число удвоений количества точек N

%в статистической серии

%Вычисляем искомый многомерный интеграл

x=rand; y=rand; z=rand; u=rand;

if u 22 » 4,2×10 6 точность лучше 10 — 4 .

Рассмотренный выше второй способ вычисления кратных интегралов менее точен, чем первый способ. Рассмотрим более подробно процедуру использования первого способа при подсчете кратных интегралов методом статистических испытаний. Обозначим через r(x,y,z) ³ 0 многомерную плотность распределения некоторой случайной величины, тогда по аналогии с одномерным случаем, имеем

. (25)

Взятие интеграла согласно способу (25) сводится к разыгрыванию многомерной случайной величины. Для разыгрывания первой переменной x построим одномерную плотность распределения по этой переменной при произвольных остальных

Функция R(x) неотрицательна и нормирована на единицу, т.е. является плотностью некоторой случайной величины, поэтому можно записать следующую формулу разыгрывания:

где g₃_i _—₂ — случайная величина, равномерно распределенная на единичном отрезке.

Найдем плотность распределения по второй координате y при фиксированной первой и произвольной третьей. Как нетрудно проверить, искомая плотность имеет вид:

В этом случае разыгрывание второй координаты сводится к решению уравнения

Плотность распределения по третьей координате z при фиксированных первых двух имеет вид:

Откуда следует последняя формула разыгрывания

В качестве примера вычисления интеграла вторым способом рассмотрим интеграл вида:

. (26)

В качестве многомерной плотности распределения возьмем функцию 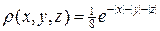. Функции r соответствуют одномерные плотности распределения вида:

(27)

С учетом (27) расчетная формула для вычисления интеграла (26) запишется в виде:

. (28)

На листинге_№11 приведен код программы численного взятия интеграла (26) с помощью первого способа в методе статистических испытаний. С учетом вида случайных величин (27), расчетная формула для искомого интеграла приведена в (28).

%Программа расчета многомерного интеграла

%(26) с помощью первого способа в методе

%статистических испытаний по расчетной

%Определяем количество удвоений числа точек

%N в серии статистических испытаний

%Определяем случайные величины xi, eta и dz,

%используемые в расчетной формуле (28)

gmxi=rand; gmeta=rand; gmdz=rand;

%Определяем искомый интеграл

%Оцениваем ошибку численного расчета

%Рисуем зависимость ошибки численного

%интегрирования от количества случайных

%точек N в статистической серии

Рис.11. Зависимость ошибки численного интегрирования при взятии
интеграла (26) от числа точек N в статистической серии

На рис.11 приведен итог работы кода программы листинга_№11. Построена кривая, описывающая зависимость ошибки численного интегрирования методом статистических испытаний от длины N статистической серии. Видно, что в среднем точность растет по мере роста числа точек в статистической серии.

Обсудим вопрос о соотношении сеточных и статистических методов численного интегрирования. Пусть функция m переменных интегрируется с помощью некоторого сеточного метода p-го порядка точности. Будем считать, что сетка по каждой из переменных имеет n узлов. В этом случае полное число узлов есть N = n m , а погрешность расчета e

n — p . Исключая n из последних двух соотношений, находим число узлов необходимое для достижения заданной точности . При использовании одного из методов статистических испытаний погрешность , т.е. число случайных точек в статистической серии .

Из сравнения двух формул и следует, что при m 2p более предпочтительными являются статистические методы. Последнее неравенство указывает на то, что для численного взятия многомерных интегралов предпочтительными являются методы статистических испытаний.

Пусть, например, подынтегральная функция имеет непрерывные вторые производные, тогда можно рассчитывать на второй порядок точности, т.е. p = 2. В этом случае трехмерные интегралы, согласно вышеупомянутым неравенствам, выгодно интегрировать сеточными методами, а пятимерные — статистическими.

Решение краевых задач

Решение краевых задач методом Монте-Карло рассмотрим на примере задачи Дирихле для уравнения Лапласа[3].

Пусть G — односвязная область, на границе которой ¶G задана функция f = f(Q), Q Î ¶G. Требуется найти такую функцию u(P), которая внутри области G удовлетворяет уравнению Лапласа:

. (29)

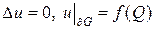
Построим в области G квадратную сетку с шагом h. Узлы данной сетки делятся на два типа: регулярные и нерегулярные (Лекция №9). Каждый регулярный узел имеет четыре соседних узла P₁, P₂, P₃, P₄ из области G согласно шаблону, приведенному на рис.7,б из лекции №9. Нерегулярный или граничный узел не имеет ровно четырех соседей из области G.

Составим разностную схему для уравнения Лапласа (29) на квадратной сетке и перепишем полученное уравнение следующим образом:

. (30)

Для решения конечно-разностной задачи (30) составим следующую теоретико-вероятностную схему. Будем считать, что величина пропорциональна плотности неких частиц в узле P. Каждая частица может с вероятностью ¼ за одни шаг по времени перейти в один из четырех соседних узлов: P₁, P₂, P₃, P₄. Таким образом, частицы, первоначально находящиеся в некотором узле, за один шаг по времени уходят из него, а другие частицы из соседних узлов могут прийти в исходный узел. Считаем, что частица, приходящая на границу области, поглощается.

Вероятность u(P,Q) того, что частица, выйдя из регулярного узла P, окончит блуждание в граничном узле Q, удовлетворяет условию (30), т.е.

(31)

и краевому условию

(32)

Если промоделировать блуждание частицы по решетке N раз, заставляя каждый раз ее выходить из точки P и подсчитывать количество L ее приходов в точку Q, то отношение является приближенным решением задачи (31) с краевыми условиями (32).

Перейдем к решению задачи Дирихле в общем случае. Пусть, когда частица оказывается в точке Q, с нее берется штраф f(Q). Величина штрафа принимает значения f(Q₁),…,f(Q_s), где Q₁,…,Q_s — совокупность всех граничных узлов. Согласно (31), (32), вероятность заплатить штраф f(Q_j) равна u(P,Q_j). Среднее значение штрафа w(P), которое заплатит произвольная частица, выходящая из регулярной точки P, определяется по формуле:

. (33)

Покажем, что выражение (33) удовлетворяет уравнению

Действительно, подставим в (31) вместо Q — Q_j и умножим обе части на f(Q_j), тогда, после суммирования по j, получим уравнение (33). Для граничных узлов функция w(P) удовлетворяет краевым условиям. Так, после подстановки P = Q в (33) согласно (32) пропадут все слагаемые, кроме одного, т.е.

т.е. w(P) удовлетворяет конечно-разностному уравнению (30) и принимает на границе заданные значения.

В качестве примера рассмотрим решение уравнения Лапласа u_xx + u_yy = 0 вида:

В качестве области интегрирования выберем единичный квадрат, т.е. G(x,y) = [0,1] 2 . Учитывая (34), определим граничные условия для задачи Дирихле

(35)

Определим квадратную сетку в единичном квадрате: x_n = h(n -1), y_m = h(m — 1), h = 1/(N — 1), n,m = 1,…,N. Регулярными и нерегулярными (граничными) будут соответственно узлы

, (36)

(36¢)

Найдем решение уравнения Лапласа (34) задачи Дирихле (35) методом Монте-Карло. Разыграем случайный процесс следующим образом. Выберем произвольный регулярный узел P из набора (36). Выпустим из этого узла частицу, и дождемся когда она, путем случайного блуждания, попадет в одну из граничных точек (36¢). Повторим эту процедуру R раз, запоминая число приходов L(P,Q) частицы в граничные точки (36¢). В итоге можно получить следующую расчетную схему:

. (37)

На листинге_№12 приведен код программы решения уравнения Лапласа (34) для задачи Дирихле в единичном квадрате (35) по расчетной схеме (37).

%Программа решения уравнения Лапласа, имеющего

%аналитическое решение (34) для задачи Дирихле

%в единичном квадрате (35) по расчетной схеме

%(37) методом Монте-Карло

%Определяем количество N узлов в сетках по

%координатам x и y

%Определяем сетки по координатам х и у

%Вносим краевые условия (35) для задачи Дирихле

%Определяем массив статистических испытаний с

%Организуем цикл статистических испытаний с разной

%длиной статистических испытаний

%Цикл статистических испытаний для каждой

%регулярной точки разностной сетки

%Определяем четыре массива для

%четырех типов граничных точек

%единичного квадрата: нижнее

%основание, правая сторона,

%верхнее основание, левая

%Статистические испытания длиной R(s)

%Цикл, моделирующий случайные

%блужданий на решетке

while (Pn>1)&(Pn 1)&(Pm 0.25)&(rnd 0.5)&(rnd 0.75

Введение

Численное решение систем линейных алгебраических уравнений (СЛАУ) одна из наиболее часто встречающихся задач в научно-технических исследованиях, математической физике (численное решение дифференциальных и интегральных уравнений), экономике, статистике. Поэтому, методам решения линейных алгебраических уравнений в современной вычислительной математике уделяется большое внимание.

Все методы решения СЛАУ делятся на две большие группы точные (прямые) и итерационные. Характерной особенностью прямых методов является возможность получить решение системы линейных уравнений за конечное число арифметических операций ( метод Гаусса , метод квадратного корня , правило Крамера и т. д.). Использование итерационных методов дает возможность найти приближенное решение системы с заданной степенью точности (метод простой итерации, метод Зейделя, метод последовательной релаксации).

Все вычислительные алгоритмы, о которых говорилось выше, являлись детерминированными. Это значит, что в любом таком алгоритме результат, получаемый на очередном шаге, точно (или с заданной погрешностью) определяется результатами, полученными на предыдущих шагах (в частности, начальными условиями). При многократной реализации детерминированного алгоритма с одними и теми же исходными данными и при отсутствии ошибок результаты, соответствующие одному и тому же шагу алгоритма, будут совпадать.

Наряду с детерминированными алгоритмами существует группа численных методов, основанных на получение большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Данная группа методов получила название методов Монте-Карло и применяется для решения задач в многочисленных областях физики, математики, экономики, оптимизации, теории управления, а также для решения основной задачи линейной алгебры — нахождения решения системы линейных алгебраических уравнений.

Данные методы интересны тем, что как показано в работах Ермакова С.М. и Данилова Д.Л. при большой размерности СЛАУ метод Монте-Карло обладает меньшей трудоемкостью (в статистическом смысле), чем детерминированные методы. Также, большое преимущество перед другими методами дает методу Монте-Карло его естественное свойство параллелизма.

Первая работа, в которой метод Монте-Карло излагался систематически, была опубликована в 1949 году Метрополисом и Уламом. В ней метод применялся для решения линейных интегральных уравнений, описывающих прохождение нейтронов через вещество.

Цели и задачи дипломного проекта. В связи с тем, что метод Монте-Карло обладает естественных параллелизмом, и развитие аппаратной поддержки параллельных вычислений получило существенное развитие в последнее время, то актуальной задачей является изучение параллельной реализации метода. Цель данного дипломного проекта состоит в исследовании метода Монте-Карло для решения СЛАУ и рассмотрении его параллельной реализации для архитектуры CUDA . Необходимо произвести тестирование реализованного алгоритма, исследовать его эффективность для решения разреженных СЛАУ больших размерностей.

Конструкторская часть.

Обзор численных методов решения систем линейных алгебраических уравнений (СЛАУ).

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) [1,2]

Будем предполагать, что определитель матрицы отличен от нуля, т.е. решение системы (1) существует.

Методы численного решения системы (1) делятся на две большие группы: прямые методы («точные») и итерационные методы.

Прямыми методами называются методы, позволяющие получить решение системы (1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.

Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (1) находится как предел последовательных приближений при , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число 0 и вычисления проводятся до тех пор, пока не будет выполнена оценка . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д. Данные методы хорошо применимы к решению разреженных матриц.

Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.

Также как прямые методы, так и итерационные в большинстве своем не обладают естественным параллелизмом, и их параллельная реализация либо требует существенного изменения алгоритма, либо основывается на работе с матрицами специального вида, допускающими независимую обработку своих элементов.

Прямые методы решения СЛАУ

Метод Гаусса

Запишем систему Ax=f, в развернутом виде

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что . Последовательно умножая первое уравнение на и складывая с i -м уравнение, исключим из всех уравнений кроме первого. Получим систему

Аналогичным образом из полученной системы исключим . Последовательно, исключая все неизвестные, получим систему треугольного вида

Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все , не равны нулю.

Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

Эта процедура получила название обратный ход метода Гаусса.

Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы А . Поэтому численная реализация метода сводится к преобразованию элементов массива размерности (m×( m +1)) , где m+1 столбец содержит элементы правой части системы.

Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.

Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность. В [1] показано, что для больших систем порядка m число действий умножений и делений близко к .

Для того чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и, следовательно, относительная погрешность будет наименьшей.

Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы 2 . Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета. Поэтому целесообразность выбора того или иного метода определяется непосредственно программистом.

Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду позволяют вычислить определитель матрицы

Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение

где Е единичная матрица. Его решение сводится к решению m систем

у вектора j я компонента равна единице, а остальные компоненты равны нулю.

Метод LU разложения

Метод LU -разложения основан на том, что если главные миноры матрицы А отличны от нуля, тогда матрицу А можно представить, причем единственным образом, в виде произведения

где L нижняя треугольная матрица с ненулевыми диагональными элементами и U верхняя треугольная матрица с единичной диагональю:

Полагая получим следующие рекуррентные формулы для вычисления элементов матрицы L и U

Если найдены матрицы L и U, то решение исходной системы (1) ID _1 сводится к последовательному решению двух систем уравнений с треугольными матрицами

Метод Холецкого (метод квадратного корня)

Метод квадратного корня по своему идейному содержанию близок к LU-методу. Основное отличие в том, что он дает упрощение для симметричных матриц. ID _1

Этот метод основан на разложении матрицы А в произведение

где S верхняя треугольная матрица с положительными элементами на главной диагонали, S T транспонированная к ней матрица.

Основываясь на выводе, предложенном в [13] получим следующее соотношение для разложения матрицы А :

В частности, при i=j получится

Далее, при i j получим

По формулам (18) и (19) находятся рекуррентно все ненулевые элементы матрицы S.

Обратный ход метода квадратного корня состоит в последовательном решении двух систем уравнений с треугольными матрицами.

Решения этих систем находятся по рекуррентным формулам (21)

Всего метод квадратного корня при факторизации A=S т S требует примерно операций умножения и деления и m операций извлечения квадратного корня.[1]

Итерационные методы решения СЛАУ

Метод простой итерации (метод Якоби)

Для того чтобы применить метод простой итерации к решению системы линейных алгебраических уравнений (1) с квадратной невырожденной матрицей A , необходимо предварительно преобразовать эту систему к виду

(23)

Здесь B квадратная матрица с элементами ,

с вектор-столбец с элементами .

Вообще говоря, операция приведения системы к виду, удобному для итерации [т.е. к виду (23)], не является простой и требует специальных знаний, а также существенного использования специфики системы. В некоторых случаях в таком преобразовании нет необходимости, так как сама исходная система уже имеет вид (23) . Часто систему (1) преобразуют к виду: , где τ специально выбираемый числовой параметр.

Выберем начальное приближение . Подставляя его в правую часть системы (23) и вычисляя полученное выражение, находим первое приближение:

Продолжая этот процесс далее, получим последовательность приближений, вычисляемых по формуле:

Для рассмотрения вопроса о сходимости метода простой итерации приведем теорему:

Теорема. Пусть выполнено условие

решение системы (23) существует и единственно;
при произвольном начальном приближении метод простой итерации сходится и справедлива оценка погрешности

Оценим трудоемкость предложенного алгоритма. Анализ расчетных фор- мул показывает, что они включают одну операцию умножения матрицы на вектор и три операции над векторами (сложение, вычитание, умножение на константу). Общее количество операций, выполняемых на одной итерации, составляет [13]:

Метод Зейделя

Пусть система (1) приведена к виду (23). Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что при вычислении очередного ( k+1) -го приближения к неизвестному при используют уже найденные ( k+1) -е приближения к неизвестным , а не k -е приближения, как в методе Якоби.

На ( k+1) -й итерации компоненты приближения вычисляются по формулам

(29)

Введем нижнюю и верхнюю треугольную матрицы:

(30)

Тогда расчетные формулы метода примут компактный вид:

Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.

Изучим сходимость метода. Для этого рассмотрим теорему.

Теорема. Пусть . Тогда при любом выборе начального приближения метод Зейделя сходится со скоростью геометрической прогрессии, знаменатель которой .

Метод релаксации

Исходная система линейных уравнений (1) приводится к виду:

(32)

Пусть — начальное приближение системы (32). Подставляя эти значения в систему (32) получим невязки

Если одной из неизвестных дать приращение , то соответствующая невязка уменьшится на величину , а все остальные невязки () увеличатся на величину . Таким образом, чтобы обратить очередную невязку в нуль достаточно величине дать приращение

Метод релаксации (по-русски: метод ослабления) [3], [4] в его простейшей форме заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.

Метод сопряженных градиентов

Рассмотрим систему линейных уравнений (1) с симметричной, положительно определенной матрицей A размера n x n. Основой метода сопряженных градиентов является следующее свойство: решение системы линейных уравнений (1) с симметричной положительно определенной матрицей A эквивалентно решению задачи минимизации функции

в пространстве R n . В самом деле, функция F ( x ) достигает своего минимального значения тогда и только тогда, когда ее градиент

обращается в ноль. Таким образом, решение системы (1) можно искать как решение задачи безусловной минимизации (38).

С целью решения задачи минимизации (38) организуется следующий итерационный процесс.

Подготовительный шаг ( s =0 ) определяется формулами

где произвольное начальное приближение, вычисляется как

Основные шаги ( s =1, 2. n -1 ) определяются формулами

Здесь невязка s -го приближения, находят из условия сопряженности

направлений и , а является решением задачи минимизации функции F по направлению

Можно показать, что для нахождения точного решения системы линейных уравнений с положительно определенной симметричной матрицей необходимо выполнить не более n итераций, тем самым, сложность алгоритма поиска точного решения имеет порядок O ( n 3 ) . Однако ввиду ошибок округления данный процесс обычно рассматривают как итерационный, процесс завершается либо при выполнении обычного условия остановки, либо при выполнении условия малости относительной нормы невязки

Общее количество числа операций, выполняемых на одной итерации, составляет [13]:

Метод бисопряженных градиентов

Пусть требуется решить систему уравнений (1). Общая идея метода бисопряженных градиентов для решения линейной системы уравнений (1) заключается в итеративной генерации пары остатков r и , вычисляемых как

где p и векторы направлений:

и выбираются таким образом, чтобы выполнялись отношения ортогональности:

Следует отметить использование матрицы M [21] в качестве матрицы предобусловливания ( preconditioner ). Использование предобусловливания во многих случаях позволяет на порядки сократить время вычислений. Причина заключается в том, что скорость сходимости итеративных методов зависит от спектральных характеристик матрицы коэффициентов. Соответственно, можно попытаться так преобразовать систему, чтобы она имела те же решения, что и исходная, но при этом имела бы лучшую (относительно метода решения) спектральную характеристику.

Выбор матрицы предобусловливания часто является достаточно сложной творческой задачей, поскольку на настоящий момент неизвестно удобных на практике формальных алгоритмов для такого выбора (хотя существует несколько наиболее распространенных вариантов [22]). Одним из наиболее распространенных является реализация предобусловливателя на основе алгоритма неполного LU -разложения [22]. Подробное описание метода приведено в [ 21, 23 ] .

Метод GMRES

Метод GMRES [20, 21] был предложен для решения несимметричных СЛАУ и основан на построении базиса в соответствующем системе подпространстве Крылова K j ( A , r 0 ) . Затем решение уточняется некоторой добавкой, представленной в виде разложения по этому базису.

В несимметричном случае основная сложность заключается в том, что для построения ортогонального базиса не могут быть использованы рекуррентные соотношения с малой глубиной зависимости типа тех, что применяются в методе сопряженных градиентов. Поэтому в GMRES ортонормальный базис < v j >строится на основе следующего соотношения, выражающего полную зависимость всех векторов:

В матрично-векторных обозначениях соотношение (54) может быть записано как

— матрица размерности в верхней форме Хессенберга.

Особенностью GMRES является то, что с целью экономии памяти выбирается некоторая размерность подпространства Крылова m (причем ), и после того как m базисных векторов построены решение уточняется. Построение очередного вектора v i обычно называют GMRES -итерацией, а m таких итераций с уточнением решения GMRES -циклом. Один цикл требует m +1 матрично-векторное умножение. Подробное описание GMRES приведено в [20, 21].

Корректность постановки задачи и понятие обусловленности

При использовании численных методов для решения тех или иных математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма, предназначенного для ее решения.

Говорят, что задача поставлена корректно , если решение существует и единственно и если оно непрерывно зависит от входных данных. Последнее свойство называется также устойчивостью относительно входных данных.

Корректность исходной математической задачи еще не гарантирует хороших свойств численного метода ее решений и требует специального исследования.

Известно, что решение задачи (1) существует тогда и только тогда, когда . В этом случае можно определить обратную матрицу и решение записать в виде .

Исследование устойчивости задачи (1) сводится к исследованию зависимости ее решения от правых частей и элементов матрицы А . Для того чтобы можно было говорить о непрерывной зависимости вектора решений от некоторых параметров, необходимо на множестве — мерных векторов принадлежащих линейному пространству H , ввести метрику.

В линейной алгебре предлагается определение множества метрик норма из которого легко получить наиболее часто используемые метрики

Подчиненные нормы матриц определяемые как

соответственно запишутся в следующем виде:

Обычно рассматривают два вида устойчивости решения системы (1):первый по правым частям, второй по коэффициентам системы(1) и по правым частям..

Наряду с исходной системой (1) рассмотрим систему с «возмущенными» правыми частями

где возмущенная правая часть системы,

Можно получить оценку, выражающую зависимость относительной погрешности решения от относительной погрешности правых частей

где число обусловленности матрицы А (в современной литературе это число обозначают как ). Если число обусловленности велико ( ), то говорят, что матрица А плохо обусловлена. В этом случае малые возмущения правых частей системы (1), вызванные либо неточностью задания исходных данных, либо вызванные погрешностями вычисления существенно влияют на решение системы. Грубо говоря если погрешность правых частей , то погрешность решения будет . Более подробно о свойствах числа обусловленности и оценке его величины можно прочитать в [3].

Если возмущение внесено в матрицу А , то для относительных возмущений решения запишем

Экспериментальное исследование устойчивости решения

При решении задач на практике часто бывает трудно оценить число обусловленности матрицы А . Поэтому существует ряд приемов, которые хотя и не дают строгий ответ об устойчивости применяемого метода и полученного решения, но все же позволяют сделать некоторые предположения о характере решения. Уточнить полученное решение и оценить его погрешность можно осуществить следующим образом.

Пусть получено приближенное решение системы (1) . Вычислим невязку уравнения . Если велико, то можно искать вектор-поправку такой, что точное решение системы . Следовательно

Можно видеть, что для нахождения поправки можно использовать алгоритм метода и соответствующую программу, по которой находилось основное решение. После этого можно уточнить решение системы . Если относительная погрешность велика, то можно повторить процесс уточнения. Если процесс уточнения, повторенный два три раза, не приводит к повышению точности, то это говорит скорей всего о том, что данная система плохо обусловлена и ее решение не может быть найдено с требуемой точностью.

Вычислительные затраты

Один из важных факторов предопределяющих выбор того или иного метода при решении конкретных задач, является вычислительная эффективность метода.

Учитывая, что операция сложения выполняется намного быстрее, чем операция умножения и деления, обычно ограничиваются подсчетом последних.

Для решения СЛАУ методом Гаусса без выбора главного элемента требуется умножений и делений, решение СЛАУ методом квадратного корня требует и m операций извлечения корней. Метод вращения предполагает вчетверо больше операций умножения, чем в методе Гаусса. При больших значениях размерности m , можно сказать, что вычислительные затраты на операции умножения и деления в методе Гаусса составляют величину , в методе квадратных корней , в методе вращений .

Общее количество операций, выполняемых на одной итерации метода Якоби, составляет [13]: . Для метода сопряженных градиентов это количество составляет: . Один цикл метода GMRES требует m +1 операций матрично-векторного умножения.

Обзор метода Монте-Карло

Идея метода

Обычный путь решения задачи состоит в том, что указывается алгоритм (последовательность действий), с помощью которого искомая величина находится или точно, или с заданной погрешностью. А именно, если через обозначить соответствующие результаты последовательно накопляющихся действий, то

причем в случае конечного числа операций процесс обрывается на некотором шаге.

Здесь процесс вычислений является строго детерминированным: два различных вычислителя при отсутствии ошибок приходят к одному и тому же результату. Однако встречаются задачи, где построение такого рода алгоритма практически невыполнимо или сам алгоритм оказывается чрезмерно сложным. В этих случаях часто прибегают к моделированию математической или физической сущности задачи и использованию законов больших чисел теории вероятностей.

Оценки искомой величины получаются на основании статистической обработки материала, связанного с результатами некоторых многократных случайных испытаний. При этом требуется, чтобы случайная величина при по вероятности сходилась к искомой величине, т. е. для любого должно иметь место предельное соотношение

где P соответствующая вероятность.

Выбор величины обусловливается конкретными особенностями задачи. Например, часто искомую величину трактуют как вероятность некоторого случайного события (или, более общо, как математическое ожидание некоторой случайной величины). Тогда частоту появления события при n соответствующих случайных испытаниях (или соответственно эмпирическое среднее значений случайной величины) в широких предположениях можно рассматривать как вероятностную оценку искомой величины. Возможны также и другие варианты. Следует заметить, что в этих случаях вычислительный процесс является недетерминированным, так как он определяется итогами случайных испытаний.

Способы решения задач, использующие случайные величины, получили общее название метода Монте-Карло, Более точно под методом Монте-Карло [6], [7], [8], [9] понимается совокупность приемов, позволяющих получать решения математических или физических задач при помощи многократных случайных испытаний. Оценки искомой величины выводятся статистическим путем и носят вероятностный характер. На практике случайные испытания заменяются результатами некоторых вычислений, производимых над случайными числами.

Случайные числа

При практическом применении метода Монте-Карло случайные испытания обычно заменяют выборкой случайных чисел.

Величина называется случайной, если она принимает те или иные значения в зависимости от появления или не появления некоторого случайного события. Случайная величина X задается законом распределения

где — любое действительное число и известная функция (функция распределения). Существует несколько основных и наиболее значимых законов распределения: равномерный и нормальный законы. Рассмотрим последовательность случайных чисел равномерно распределенных на отрезке ( a , b ). Для такой последовательности имеет место соотношение

где число элементов последовательности , принадлежащих промежутку ( a , b ).

Следует заметить, что, имея случайную последовательность , равномерно распределенную на отрезке [0, 1], можно построить случайную последовательность с заданным законом распределения Ф(у) .

Для решения задач методом Монте-Карло обычно требуется весьма большое количество случайных чисел. Эти числа практически наиболее удобно получаются с помощью специальных датчиков случайных чисел, подключаемых к машине. Действие этих датчиков регулируется случайными физическими процессами (например, радиоактивным распадом, шумами в электронных лампах и т. п.) [9].

Так как воспроизводство случайных чисел, отвечающих данной теоретической модели, есть процесс весьма тонкий и сложный, то на практике часто ограничиваются получением, так называемых псевдослучайных чисел, в основных чертах похожих на соответствующие случайные. Источниками (датчиками) псевдослучайных чисел служат достаточно сложные математические алгоритмы.

При решении СЛАУ больших размерностей методом Монте-Карло требуется создавать n -мерные последовательности, при этом генератор псевдослучайных чисел часто не может создавать достаточно равномерно распределенные последовательности. В таких ситуациях возможно пожертвовать «случайностью» и создавать последовательности с более равномерным покрытием области. Числа, полученные в результате таких действий, называются квазислучайными (КСЧ). В ряде задач (например, в задаче численного интегрирования) применение последовательностей КСЧ обеспечивает существенно лучшую сходимость по сравнению с реализациями метода Монте-Карло, основанными на использовании псевдослучайных чисел (ПСЧ) [14].

В качестве иллюстрации приведем диаграмму расположения случайных и псевдослучайных точек в двумерной области. Данный рисунок наглядно подтверждает большую равномерность покрытия области квазислучайными точками по сравнению с псевдослучайными.

Рис. 1. Псевдо и квазислучайные точки

Описание метода

Пусть исходная система уравнений записана в виде:

где B квадратная матрица размерности n х n , обладающая диагональным приобладанием,

x вектор неизвестных,

f вектор значений правой части системы.

Приведем систему (67) к виду:

Будем полагать, что для системы (2) имеет место соотношение:

От системы (67) к системе (68) можно перейти с помощью следующих преобразований. Пусть для фиксированного i . Если в i -м уравнении системы (1) коэффициент , то делим каждый член этого уравнения на L , в противном случае на L . Обозначим и . Полученные числа и будут коэффициентами системы (68) [13].

Сопоставим теперь i -му уравнению этой системы разбиение отрезка [0…1] на n +1 отрезков точками s j , каждая из которых имеет координату, определяемую соотношениями . Положим .

Рассмотрим процесс «случайного блуждания» некоторой частицы, которая в начальный момент находится в точке i -го разбиения отрезка [0; 1] (диагональный элемент i -й строки). Воспользуемся возможностью получения случайных чисел, равномерно распределенных на отрезке [0; 1], рассмотрим такое случайное число c . Если оно удовлетворяет соотношению для точек рассматриваемого i -го разбиения, то считаем, что частица переходит из точки i -го разбиения в точку j -го разбиения (на j -ю строку, диагональный элемент).

Снова получаем случайное число и рассматриваем его положение относительно точек текущего j -го разбиения. Если в этом разбиении полученное число лежит на отрезке , то считаем, что частица переходит из точки j -го разбиения в точку k -го разбиения. В том случае, когда для некоторого разбиения очередное случайное число попадает на отрезок , считаем, что частица переходит в точку и процесс случайного блуждания заканчивается.

Последовательность точек назовем траекторией частицы. Свяжем с этой траекторией случайную величину , задаваемую соотношением , где , а величина .

Доказано [8, 11, 12], что математическое ожидание случайной величины равно значению корня системы уравнений. Осуществим М реализаций случайного блуждания частицы по траектории, начинающейся в точке . Обозначим через Y сумму значений случайной величины , полученных во всех реализациях, т.е. . Тогда будем иметь приближенное равенство

Более наглядное представление о структуре алгоритма можно получить, если обратиться к блок-схеме метода, представленной на рисунке 2.

Рис.2. Блок-схема метода Монте-Карло

Рассмотрим более подробно создание цепи Маркова. Для этого обратимся к схеме алгоритма создания цепи Маркова представленной в псевдокоде:

Входные данные: root , p , v , offsets , colInd , w ;

целое curEq := root ;

создать равномерно распределенное случайное число rNum ;

if( rNum p[offsets[curEq] + j] )

vv := vv*v[offsets[curEq] + j];

curEq := colInd[offsets[curEq] + j];

if( isFound != true )

Входными данными являются указатели на массивы, содержащие элементы матрицы переходов ( p ), знаки коэффициентов исходной системы ( v ), строковые указатели ( offsets ), столбцовые индексы ( colInd ), элементы вектора весов ( w ). Результат записывается в вещественную переменную y .

Следует заметить, что метод Монте-Карло обладает естественным параллелизмом: существует возможность независимого параллельного вычисления как различных корней системы линейных алгебраических уравнений, так и оценок каждого корня. В настоящее время основной акцент в развитии вычислительной техники делается на многопроцессорные системы, поэтому стремительно развиваются всевозможные параллельные методы Монте-Карло, расширяется область их применения.

Еще одна особенность метода Монте-Карло состоит в том, что он существенным образом зависит от возможности генератора ПСЧ сгенерировать достаточно много «хороших» последовательностей. Таким образом, выбор качественного генератора псевдослучайных чисел является очень важным моментом при реализации данного метода.

Разработка параллельной реализации метода Монте-Карло для решения СЛАУ для архитектуры CUDA

Одним из хорошо известных преимуществ метода Монте-Карло является высокая эффективность, с которой он может быть распараллелен. Различные процессы (нити) могут создавать независимые случайные блуждания и получать при помощи них свои собственные оценки искомой величины (или корня СЛАУ в рассматриваемом случае). Далее необходимо собрать эти «индивидуальные» оценки для получения конечного результата.

Как уже ранее было замечено, параллельные методы Монте-Карло существенным образом зависят от возможностей генератора ПСЧ. В дополнение к свойствам, которым должен обладать последовательный генератор, должны выполняться также следующие свойства:

Независимость: числа из различных последовательностей должны быть не коррелированны.
Масштабируемость: нужно уметь генерировать столько последовательностей, сколько нужно для работы с большим числом потоков.

Рассмотрим некоторые подходы к распараллеливанию метода Монте-Карло [14].

Подход «мастер-рабочий»

Очевидным способом распараллеливания метода Монте-Карло является метод «мастер-рабочий». Поток-мастер, используя генератор, порождает последовательность случайных чисел, и распределяет полученные числа по рабочим потокам.

Можно отметить несколько недостатков метода «мастер-рабочий», первый из которых заключается в следующем. Некоторые генераторы порождают последовательности, автокоррелированные с большим шагом. Но так как каждый поток получает числа из единственной последовательности, корреляция с большим лагом в одной последовательности может стать корреляцией с малым шагом в параллельных последовательностях.

Второй недостаток заключается в том, что метод «мастер-рабочий» плохо масштабируется на произвольное число потоков. Сложно сбалансировать скорость работы генератора случайных чисел в потоке-мастере со скоростью обработки этих чисел в потоках-рабочих. Если обработка очередного случайного числа является трудоемкой (по сравнению с его генерацией), то потоки-рабочие не будут справляться с обработкой потока поступающих чисел. В противном случае потоки-рабочие будут простаивать, ожидая, пока мастер сгенерирует очередное случайное число.

Эти недостатки делают данный подход практически неприемлемым, особенно для SIMD архитектуры.

Метод с перешагиванием

Метод с перешагиванием аналогичен циклической схеме распределения данных по потокам. Предположим, что метод Монте-Карло выполняется в p -поточной программе. Каждый поток имеет свою копию одного и того же генератора случайных чисел, порождающего последовательность X n ; при этом i -й поток обрабатывает каждое p -е число последовательности, начиная с X i :

X i , X i+p , X i+2p ,…

На рис. 3 изображены элементы последовательности, генерируемые методом во 2-м потоке 4-х поточной программы

Рис. 3. элементы последовательности, генерируемые методом во 2-м потоке 4-х поточной программы

Рассмотрим недостатки данного подхода. Во-первых, метод с перешагиванием не приспособлен для динамического создания новой последовательности случайных чисел в новом потоке, т.к. каждое число последовательности заранее «закреплено» за определенным потоком.

Во-вторых, даже если исходная последовательность случайных чисел была не коррелирована, то элементы полученных подпоследовательностей могут быть коррелированны для некоторых значений p . В общем случае корреляция на больших промежутках в исходной последовательности может превратиться в корреляцию на малых промежутках в параллельных подпоследовательностях.

Разделение последовательностей

Метод разделения последовательности аналогичен блочной схеме распределения данных между потоками. Пусть T период используемого генератора случайных чисел, а длина последовательности, которую мы хотим обработать. Тогда последовательность длины N разделяется на подпоследовательности равной длины по одной для каждого из p потоков. В этом случае каждый поток работает с непрерывной частью исходной последовательности.

Рис. 4. Разделение последовательности

Сложностью данного метода является необходимость вычислять -й член последовательности как начальный элемент в i -м потоке, что вообще говоря, является трудоемкой операцией. С другой стороны, это нужно делать лишь однократно, а затем можно генерировать элементы последовательности по порядку.

Параметризация

Следующий подход к параллельной генерации случайных чисел состоит в использовании в разных потоках разных независимых случайных последовательностей. Например, для генерации p последовательностей можно взять p разных генераторов, основанных на разных принципах. Последовательности, полученные данным способом, будут независимыми, но это решение не будет масштабируемым, т.к. число различных генераторов невелико.

Добиться масштабируемости можно при использовании одного и того же генератора случайных чисел, но с разными входными параметрами (параметризация). Естественно, при этом нужно убедиться в том, что сгенерированные подобным образом последовательности будут независимыми. В общем случае этого гарантировать нельзя, все зависит от конкретной реализации генератора псевдослучайных чисел.

Выбор подхода для параллельной реализации

Рассмотрим описанные выше подходы с точки зрения их применимости к SIMD архитектуре CUDA . Для этого необходимо обратить внимание на некоторые ограничивающие особенности данной архитектуры. Так ядро, отвечающее за выполнение случайных блужданий, должно содержать как можно меньше инструкций и обращений к регистровой памяти, так как ресурсы данного типа памяти весьма ограничены в пределах блока.

Ввиду того, что как правило, тактовая частота мультипроцессора графического адаптера невелика, выполнение большого количества сложных ядер, содержащих большое количество инструкций, может привести к падению производительности.

Из-за специфики SIMD архитектуры нет возможности использовать различные генераторы псевдослучайных чисел в различных нитях и блоках. Кроме того рекомендуется чтобы сам генератор обладал как можно меньшим количеством параметров, необходимых для его инициализации и хранения его состояния, потому как данный набор параметров необходимо хранить между различными вызовами генератора. Таким образом, подходы «мастер-рабочий», «параметризация» и «метод с перешагиванием» не подходят по совокупности причин.

Рассмотрим подход «Разделение последовательностей» с точки зрения SIMD архитектуры CUDA . Одним из недостатков данного подхода является сложность вычисления -го члена последовательности как начального элемента в i -м потоке (нити, в терминах архитектуры CUDA ). Однако генераторы, предоставляемые библиотекой CURAND , обладают встроенной возможностью определения подпоследовательности, соответствующей конкретной нити.

При использовании библиотеки CURAND в качестве генератора «по умолчанию» используется генератор XORWOW, обладающий периодом 2 192 -1. В случае использования данного генератора на каждую подполседовательность приходится 2 67 случайных чисел [18]. Данный генератор использует относительно «легковесную» структуру данных для хранения своего состояния, что также является его преимуществом. Таким образом, подход с разделением последовательностей является оптимальным с точки зрения SIMD архитектуры CUDA .

Параллельная реализация метода Монте-Карло

В связи с ограничениями архитектуры CUDA , а именно ограниченности памяти, доступной конкретной нити, вычисление матрицы переходов и вектора весов следует провести отдельно. Таким образом, ядро CUDA будет выполнять построение цепи Маркова, и осуществлять процесс случайного блуждания.

Так как метод обладает естественным параллелизмом, то будем осуществлять вычисление каждого корня СЛАУ в соответствующем блоке, внутри блока будем вычислять «индивидуальные» оценки корня СЛАУ. Размерность блока примем равной максимально возможной для данного графического адаптера. Более наглядно структуру программы можно изучить, обратившись к рис. 5.

Анализ матрицы, преобразование матрицы к виду x=Ax+f , проверка нормы преобразованной матрицы

Расчет матрицы перехода и вектора весов

Запуск ядра для расчета корней СЛАУ

Отправка матрицы переходов, вектора весов на графический адаптер

Чтение матрицы коэффициентов СЛАУ из формата Matrix Market

Запись результатов в файл

Рис. 5. Структура программы

На вход программа получает имя файла с разреженной матрицей, хранящейся в формате Matrix Market . Далее при помощи библиотеки CUSP производится считывание файла во внутренний формат программы разреженный строчный формат, удобный для обработки методом Монте-Карло.

Рассмотрим блок-схему ядра CUDA , реализующего оценку конкретного корня СЛАУ, представленную на рис. 6. На вход ядро получает указатели на массивы описывающие матрицу переходов и знаков в строчном разреженном формате, а также вектор весов, зерно для генератора случайных чисел и указатель на массив результатов. Внутри ядра каждая нить определяет свой глобальный и локальный индексы и в соответствии с ними происходит инициализация генератора случайных чисел, например, так:

где gid глобальный индекс нити, seed зерно генератора случайных чисел, localState структура, хранящая состояние генератора. В данной реализации метода Монте-Карло в качестве генератора случайных чисел использовался генератор XORWOW , его подробное описание можно найти в [17].

Далее выполняется процедура барьерной синхронизации нитей внутри одного блока, и они приступают к созданию цепей Маркова для оценки корня СЛАУ. Так как каждая нить совершает оценок корня, то необходимо просуммировать результаты полученные отдельными нитями. Данная процедура также выполняется параллельно при помощи алгоритма свертки массива, представленного на рис. 7.

Рис. 6. Блок-схема ядра

Рис. 7. Свертка массива

Технологическая часть. Разработка программного обеспечения реализующего метод Монте-Карло для решения СЛАУ

Обзор используемых технологий и программных платформ

Технология NVIDIA CUDA

Рассмотрим некоторые существенные отличия между областями и особенностями применений центрального процессора и видеокарты.

Центральный процессор ( CPU ) изначально приспособлен для решения задач общего плана и работает с произвольно адресуемой памятью. Программы могут обращаться напрямую к любым ячейкам линейной и однородной памяти.

Для графического адаптера (GPU) это не так. В архитектуре CUDA имеется 6 различных видов памяти. Читать можно из любой ячейки, доступной физически, но вот записывать не во все ячейки. Причина заключается в том, что графический адаптер в общем случае представляет собой специфическое устройство, предназначенное для конкретных целей. Это ограничение введено ради увеличения скорости работы определенных алгоритмов и снижения стоимости оборудования.

Одна из основных проблем большинства вычислительных систем заключается в том, что память работает медленнее процессора. Для центрального процессора она решается путем введения кэш-памяти. Наиболее часто используемые участки памяти помещается в сверхоперативную или кэш-память, работающую на частоте процессора. Это позволяет сэкономить время при обращении к наиболее часто используемым данным и загрузить процессор собственно вычислениями.

Необходимо заметить, что кэш-память для программиста фактически прозрачна. Как при чтении, так и при записи данные не попадают сразу в оперативную память, а проходят через нее. Это позволяет, в частности, быстро считывать некоторое значение сразу же после записи.

На GPU (здесь и далее подразумевается видеокарты GF восьмой серии и выше) кэш-память тоже есть, и она тоже важна, но этот механизм не такой мощный, как на CPU. Во-первых, кэшируется не все типы памяти, а во-вторых, кэш-память работает только на чтение.

На GPU медленные обращения к памяти скрывают, используя параллельные вычисления. Пока одни задачи ждут данных, работают другие, готовые к вычислениям. Это один из основных принципов CUDA, позволяющих сильно поднять производительность системы в целом.

Вычислительная архитектура CUDA основана на концепции одна команда на множество данных (Single Instruction Multiple Data, SIMD) и понятии мультипроцессора [15]. Концепция SIMD подразумевает, что одна инструкция позволяет одновременно обработать множество данных.

Мультипроцессор это многоядерный SIMD процессор, позволяющий в каждый определенный момент времени выполнять на всех ядрах только одну инструкцию. Каждое ядро мультипроцессора скалярное, т.е. оно не поддерживает векторные операции в чистом виде.

Для дальнейшего рассмотрения архитектуры CUDA необходимо ввести такие понятия как хост ( host ) и устройство ( device ). Устройством (device) является видеоадаптер, поддерживающий драйвер CUDA, или другое специализированное устройство, предназначенное для исполнения программ, использующих CUDA (такое, например, как NVIDIA Tesla). Рассмотрим GPU только как логическое устройство, избегая конкретных деталей реализации.

Хост (host) это программа в обычной оперативной памяти компьютера, использующая CPU и выполняющая управляющие функции по работе с устройством. Фактически, та часть программы, которая работает на CPU это хост, а видеокарта устройство. Логически устройство можно представить как набор мультипроцессоров (рис.8) плюс драйвер CUDA.

Рис. 8. Устройство

Предположим, что необходимо запустить на устройстве некую процедуру в N потоках. В соответствии с документацией CUDA, данная процедура называется ядром.

Особенностью архитектуры CUDA является блочно-сеточная организация, необычная для многопоточных приложений (рис. 9). При этом драйвер CUDA самостоятельно распределяет ресурсы устройства между потоками.

Рис. 9. Организация потоков

На рис. 9. изображено ядро. Все потоки, выполняющие это ядро, объединяются в блоки, а блоки, в свою очередь, объединяются в сетку.

Как видно на рис. 9, для идентификации потоков используются двухмерные индексы. Разработчики CUDA предоставили возможность работать с трехмерными, двухмерными или простыми (одномерными) индексами, в зависимости от того, как удобно программисту. В общем случае индексы представляют собой трехмерные векторы. Для каждого потока будут известны: индекс потока внутри блока threadIdx и индекс блока внутри сетки blockIdx. При запуске все потоки будут отличаться только этими индексами. Фактически, именно через эти индексы программист осуществляет управление, определяя, какая именно часть его данных обрабатывается в каждом потоке.

Ответ на вопрос, почему разработчики выбрали именно такую организацию, нетривиален. Одна из причин состоит в том, что один блок гарантировано исполняется на одном мультипроцессоре устройства, но один мультипроцессор может выполнять несколько различных блоков.

Блок задач (потоков) выполняется на мультипроцессоре частями, или пулами, называемыми warp. Размер warp на текущий момент в большинстве видеокарт с поддержкой CUDA равен 32 потокам. Задачи внутри пула warp исполняются в SIMD стиле, т.е. во всех потоках внутри warp одновременно может выполняться только одна инструкция.

Разработчики CUDA не регламентируют жестко размер warp. В своих работах они упоминают параметр warp size. Во-вторых, с логической точки зрения именно warp является тем минимальным объединением потоков, про который можно говорить, что все потоки внутри него выполняются одновременно и при этом никаких допущений относительно остальной системы сделано не будет.

Сразу же возникает вопрос: если в один и тот же момент времени все потоки внутри warp исполняют одну и ту же инструкцию, то как быть с ветвлениями? Ведь если в коде программы встречается ветвление, то инструкции будут уже разные. Здесь применяется стандартное для SIMD программирования решение (рис 10).

Пусть имеется следующий код:

В случае SISD (Single Instruction Single Data) мы выполняем оператор A, проверяем условие, затем выполняем операторы B и D (если условие истинно).

Пусть есть 10 потоков, исполняющихся в стиле SIMD. Во всех 10 потоках выполняется оператор A, затем проверяем условие cond и оказывается, что в 9 из 10 потоках оно истинно, а в одном потоке ложно.

Рис. 10. Организация ветвления в SIMD

Понятно, что мы не можем запустить 9 потоков для выполнения оператора B, а один оставшийся для выполнения оператора C, потому что одновременно во всех потоках может исполняться только одна инструкция. В этом случае нужно поступить так: сначала «убиваем» отколовшийся поток так, чтобы он не портил ничьи данные, и выполняем 9 оставшихся потоков. Затем «убиваем» 9 потоков, выполнивших оператор B, и проходим один поток с оператором C. После этого потоки опять объединяются и выполняют оператор D все одновременно.

Получается, что мало того, что ресурсы процессоров расходуются на пустое перемалывание битов в отколовшихся потоках, так еще, что гораздо хуже, придется в итоге выполнить ОБЕ ветки.

Однако следует заметить, что эти инструкции выполняются динамически драйвером CUDA и для программиста они совершенно прозрачны.

Ветвления не являются причиной падения производительности сами по себе. Вредны только те ветвления, на которых потоки расходятся внутри одного пула потоков warp. При этом если потоки разошлись внутри одного блока, но в разных пулах warp, или внутри разных блоков, это не оказывает ровным счетом никакого эффекта.

Любое взаимодействие между потоками (синхронизация и обмен данными) возможно только внутри блока. То есть между потоками разных блоков нельзя организовать взаимодействие, пользуясь лишь документированными возможностями.

Синхронизация всех задач внутри блока осуществляется вызовом функции __synchtreads(). Обмен данными возможен через разделяемую память, так как она общая для всех задач внутри блока.

Рис. 11. Иерархия памяти в архитектуре CUDA

В архитектуре CUDA выделяют шесть видов памяти [16, 17] (рис. 11). Это регистры, локальная, глобальная, разделяемая, константная и текстурная память. Такое обилие обусловлено спецификой видеокарты и первичным ее предназначением, а также стремлением разработчиков сделать систему как можно дешевле, жертвуя в различных случаях либо универсальностью, либо скоростью.

По возможности компилятор старается размещать все локальные переменные функций в регистрах. Доступ к таким переменным осуществляется с максимальной скоростью. В текущей архитектуре на один мультипроцессор доступно 8192 32-разрядных регистра. Для того чтобы определить, сколько доступно регистров одному потоку, надо разделить это число (8192) на размер блока (количество потоков в нем). При обычном разделении в 64 потока на блок получается всего 128 регистров (существуют некие объективные критерии, но 64 подходит в среднем для многих задач).

Если учесть, что на одном мультипроцессоре может исполняться несколько блоков, то для большей эффективности надо стараться занимать меньше 64 или даже меньше 32 регистров. Тогда теоретически может быть запущено 4 блока на одном мультипроцессоре. Однако здесь еще следует учитывать объем разделяемой памяти, занимаемой потоками, так как если один блок занимает всю разделяемую память, два таких блока не могут выполняться на мультипроцессоре одновременно

В случаях, когда локальные данные процедур занимают слишком большой размер, или компилятор не может вычислить для них некоторый постоянный шаг при обращении, он может поместить их в локальную память. Этому может способствовать, например, приведение указателей для типов разных размеров. Физически локальная память является аналогом глобальной памяти, и работает с той же скоростью. На данный момент нет никаких механизмов, позволяющих явно запретить компилятору использование локальной памяти для конкретных переменных. Так как проконтролировать локальную память довольно трудно, лучше стараться не использовать ее вовсе.

В документации CUDA [17] в качестве одного из основных достижений технологии приводится возможность произвольной адресации глобальной памяти. То есть можно читать из любой ячейки памяти, и писать можно тоже в произвольную ячейку (в общем случае на GPU это обычно не так). Однако за универсальность в данном случае приходится расплачиваться скоростью. Глобальная память не кэшируется. Она работает очень медленно, количество обращений к глобальной памяти следует в любом случае минимизировать.
Глобальная память необходима в основном для сохранения результатов работы программы перед отправкой их на хост (в обычную оперативную память графического адаптера). Причина этого в том, что глобальная память единственный вид памяти, куда можно что-то записывать.

Переменные, объявленные с квалификатором __global__, размещаются в глобальной памяти. Глобальную память также можно выделить динамически, вызвав функцию cudaMalloc(void* mem, int size) на хосте. Из устройства эту функцию вызывать нельзя. Отсюда следует, что распределением памяти должна заниматься программа-хост, работающая на CPU. Данные с хоста можно отправлять в устройство вызовом функции cudaMemcpy:

cudaMemcpy(void* gpu_mem, void* cpu_mem, int size, cudaMemcpyHostToDevice);

Точно таким же образом можно проделать и обратную процедуру:

cudaMemcpy(void* cpu_mem, void* gpu_mem, int size, cudaMemcpyDeviceToHost);

Этот вызов тоже осуществляется с хоста.

Разделяемая память это некэшируемая, но быстрая память. Ее следует использовать как управляемый кэш. На один мультипроцессор доступно всего порядка 16 Кб разделяемой памяти. Разделив это число на количество задач в блоке, можно получить максимальное количество разделяемой памяти, доступной на один поток (если планируется использовать ее независимо во всех потоках). Отличительной чертой разделяемой памяти является то, что она адресуется одинаково для всех задач внутри блока (рис. 5). Отсюда следует, что ее можно использовать для обмена данными между потоками только одного блока.

Гарантируется, что во время исполнения блока на мультипроцессоре содержимое разделяемой памяти будет сохраняться. Однако после того как на мультипроцессоре сменился блок, не гарантируется, что содержимое старого блока сохранилось. Поэтому разработчику не стоит пытаться синхронизировать задачи между блоками, оставляя в разделяемой памяти какие-либо данные и надеясь на их сохранность.
Переменные, объявленные с квалификатором __shared__, размещаются в разделяемой памяти.

__shared__ float mem_shared[N_THREADS];

Следует еще раз подчеркнуть, что разделяемая память для блока одна. Поэтому если нужно использовать ее просто как управляемый кэш, следует обращаться к разным элементам массива, например:

float x = mem_shared[threadIdx.x];

Где threadIdx.x индекс x потока внутри блока.

Константная память кэшируется, как это видно на рис. 8. Кэш существует в единственном экземпляре для одного мультипроцессора, а следовательно, он общий для всех задач внутри блока. На хосте в константную память можно что-то записать, вызвав функцию cudaMemcpyToSymbol. Из устройства константная память доступна только для чтения. Константная память очень удобна в использовании. Можно размещать в ней данные любого типа и читать их при помощи простого присваивания.

Так как для константной памяти используется кэш, доступ к ней в общем случае довольно быстрый. Единственный, но очень большой недостаток константной памяти заключается в том, что ее размер составляет всего 64 Kб (на все устройство). Из этого следует, что в константной памяти имеет смысл хранить лишь небольшое количество часто используемых данных.

Текстурная память кэшируется (рис. 8). Для каждого мультипроцессора имеется только один кэш, а значит, этот кэш общий для всех задач внутри блока. Название текстурной памяти и функциональность унаследованы от понятий «текстура» и «текстурирование». Текстурирование это процесс наложения текстуры (картинки) на полигон в процессе растеризации. Текстурная память оптимизирована под выборку 2D данных и имеет следующие возможности:

быстрая выборка значений фиксированного размера (байт, слово, двойное или учетверенное слово) из одномерного или двухмерного массива;
нормализованная адресация числами типа float в интервале [0,1).
аппаратная линейная или билинейная (в случае 2D) интерполяция соседних значений в случае нормализованной адресации;
аппаратная обработка выхода за границу массива с использованием двух режимов: clamp и wrap;

Текстурная память физически не отделена от глобальной памяти. Выделив функцией cudaMalloc некий участок глобальной памяти, можно затем указать с помощью функции cudaBindTexture, что данный участок теперь будет рассматриваться как текстурная память. Таким образом, получается, что размер текстурной памяти ограничивается только максимальным размером памяти, которую может выделить устройство (в общем случае сотни мегабайт).

Из недостатков текстурной памяти следует отметить, что из нее можно читать данные только встроенных в компилятор nvcc типов, имеющих размер 1, 2, 4, 8 или 16 байт, и только с помощью специальных функций tex1D, tex2D или tex1Dfetch, tex2Dfetch. Иначе говоря, нельзя сделать указатель на текстурную память и получить его адрес произвольным образом (например, прочитав какую-либо структуру размером в 26 байт).

В отличие от текстурной памяти с константной памятью так обращаться можно, и поэтому обращения к константной памяти в коде программного обеспечения выглядят вполне приемлемо и никак не выделяются. Для того чтобы воспользоваться объектом или структурой в текстурной памяти, его необходимо сначала скопировать из нее (с помощью функции tex1Dfetch) в регистровую или разделяемую память, затем данный объект или текстуру можно использовать.

Далее необходимо объяснить термин нормализованная адресация. Нормализованная адресация это адресация числом с плавающей точкой от 0 до 1. При нормализованной адресации на финальной стадии производится дискретизация float индекса. В этой ситуации можно либо выбрать ближайший элемент, либо провести интерполяцию между соседними элементами. Интерполяцию можно использовать только в том случае, если текстура выбирается значениями float. При этом допускаются векторизованные типы и типы, отличные от типов с плавающей точкой.

Например, можно создать текстуру с элементами uchar4, находящимися в интервале [0,255]. Затем можно их выбирать, используя нормализованную адресацию. Результатом будет значение типа float4, отображенное в интервал [0,1). Здесь используется стандартное математическое обозначение для интервала, где 0 включается, а 1 нет.

Архитектура CUDA позволяет сделать обработку выхода за границы массива в двух режимах wrap и clamp. При использовании режима clamp происходит «схлопывание» значения до ближайшей границы. В режиме wrap координаты заворачиваются таким образом, что если координата x выходит за границу массива на N, то будет взят N-ый элемент массива. Т.е. фактически всегда берется остаток от деления на размер массива. Следует отметить, что это свойство текстурной памяти весьма полезно для реализации хэш-таблиц.

Библиотека CURAND

Библиотека входит в стандартный комплект разработчика программного обеспечения CUDA и представляет собой набор заголовочных файлов [18]. Данная библиотека предоставляет набор инструментов для простого и быстрого создания последовательностей псевдо и квази случайных чисел. Последовательность псевдослучайных чисел удовлетворяет большинству статистических свойств случайных последовательностей.

Библиотека CURAND функционально состоит из двух частей: библиотеки для хоста (центрального процессора) и библиотеки для устройства (графический адаптер).

Первая предоставляет возможность создания случайных чисел, как при помощи центрального процессора, так и при помощи графического адаптера. В первом случае случайные числа хранятся в адресном пространстве доступном центральному процессору. При втором варианте вызов библиотеки происходит со стороны хоста, а основная работа по созданию случайных чисел происходит на графическом адаптере, и полученный результат работы хранится в его оперативной памяти.

Далее пользователь может использовать результаты в своих ядрах, либо отправить их в память центрального процессора. Для большей наглядности рассмотрим типичную последовательность действий по созданию последовательностей случайных чисел при использовании библиотеки для хоста:

Создать генератор требуемого типа при помощи функции curandCreateGenerator()
Установить опции генератора, например, использовать функцию curandSetPseudoRandomGeneratorSeed() для установки ключа (зерна)состояния генератора
Выделить память графического адаптера при помощи вызова cudaMalloc()
Создать случайные числа при помощи функции curandGenerate(), либо при помощи любой другой функции, обеспечивающей создание последовательностей случайных чисел
Каким-либо требуемым образом использовать полученные случайные числа
Если требуется, то создать больше случайных чисел
Очистить используемые ресурсы при помощи curandDestroyGenerator()

Вторая важная часть библиотеки определяет вызовы функций для создания последовательностей случайных чисел непосредственно на графическом адаптере. Пользователь может включать вызовы этих функций непосредственно в код разрабатываемых ядер, при этом результат не требует хранения в оперативной памяти графической карты и может сразу быть использован в последующих операциях ядра. Библиотека определяет вызовы как для установки и инициализации функций, создающих последовательности случайных чисел, так и сами функции.

Рассмотрим более подробно библиотеку для устройства. Для ее использования необходимо подключить заголовочный файл curand _ kernel . h >. Данный файл содержит функции для создания последовательностей псевдо и квази случайных чисел. Псевдослучайные числа могут быть созданы при помощи различных генераторов, предоставляемых данной библиотекой (XORWOW, MRG32k3a, MTGP32), так же возможно создание последовательностей подчиняющихся определенным законам распределения (равномерное, нормальное) [18]. Для создания квази случайных чисел в библиотеки используются функции на основе последовательности Соболя.

Библиотека CUSP

Данная библиотека также поставляется вместе с инструментами разработчика CUDA и представляет собой библиотеку шаблонов Си++. Она предоставляет широкие возможности по работе с разреженными ( sparse ) матрицами: хранение в различных форматах, конвертации между различными форматами, чтение и запись матриц из формата Matrix market (файлы . mtx ), умножение матриц, хранящихся в разреженном формате между собой и заполненными векторами и многое другое [19]. Разработчиками реализованы следующие форматы хранения разреженных матриц:

Разреженный строчный формат
Разреженный столбцовый формат
Диагональный (для хранения диагональных матриц)
ELL
Гибридный ( Hybrid )

При использовании матриц, хранящихся в разных форматах, важно понимать преимущества и недостатки каждого формата. Вообще говоря, Диагональный и ELL форматы хранения являются наиболее эффективными для расчета различных операций над разреженными матрицами и векторами, сводящимися к скалярному произведению строк разреженной матрицы на вектор, и, следовательно, являются самыми быстрыми форматы для решения разреженных линейных систем при помощи итерационных методов (например, метод сопряженных градиентов).

Разреженные строчный и столбцовые форматы являются более гибкими и простыми в использовании, чем диагональный и EL . Гибридный формат ( HYB ) представляет собой сочетание формата ELL (быстрый) и разреженного столбцового (гибкий) и является хорошим выбором «по умолчанию».

Исследовательская часть. Тестирование параллельной реализации метода Монте-Карло и анализ результатов.

Постановка эксперимента

В ходе экспериментов проводилось решение СЛАУ (1), в которой в качестве матрицы коэффициентов системы использовались различные матрицы, получающиеся при решении прикладных задач. Были использованы матрицы со следующих сайтов [24, 25].

Как было замечено в параграфе с описанием метода (2.7.3) для возможности решения СЛАУ методом Монте-Карло необходимо, чтобы матрица коэффициентов системы обладала диагональным преобладанием. Поэтому в случае если исходная матрица не обладает диагональным преобладанием, то производится преобразование матрицы к виду с диагональным преобладанием. Для этого к диагональному элементу каждой строки прибавляется сумма модулей недиагональных элементов данной строки со знаком диагонального элемента.

Вектор свободных частей системы (1) определялся следующим образом. Зададим вектор точного решения СЛАУ (1):

Тогда, умножив матрицу коэффициентов на вектор точного решения x , получим искомый вектор b :

Обзор использованных матриц

Для большей наглядности сведем данные о матрицах в таблицу 1:

Таблица 1. Использованные матрицы

Приведем наглядное изображение структуры использованных матриц:

Рис. 12. Структура матрицы s1rmq4m1

Рис. 13. Структура матрицы bcsstk17

Рис. 14. Структура матрицы fidapm29

Рис. 15. Структура матрицы fidapm11

Рис. 16. Структура матрицы s3dkt3m2

Рис. 17. Структура матрицы BenElechi1

Конфигурация использованного оборудования

Для проведения экспериментов использовался компьютер со следующими характеристиками:

Процессор: Intel ( R ) Core 2 Quade Q 9000, количество ядер 4, частота ядра 2 ГГц.

Видеокарта: NVIDIA GeForce GT 240 M , Compute Capability 1.2, количество мультипроцессоров 6, частота 1,21 ГГц.

Методика проведения экспериментов

Проводилось решение СЛАУ с матрицами коэффициентов и свободными частями описанными выше. Решение проводилось тремя различными методами: исследуемым методом Монте-Карло, методом GMRES и методом бисопряженных градиентов ( BICG ) из библиотеки CUSP . Измерялось время расчетов на графической карте при помощи механизма событий CUDA . Для всех матриц, кроме матриц BenElechi1и s3dkt3m2, выполнялось 5 запусков, в результатах использованы средние значения. Для BenElechi1и s3dkt3m2 выполнялось 3 запуска.

Для метода Монте-Карло проводились расчеты с количеством реализаций случайного процесса 1000000. На графической карте выполнялись расчеты корней СЛАУ блоками по 100. Для методов GMRES и BICG использовались следующие критерии остановки: достижение количества итераций 10000 или достижение точности 10 -6 .

Также был проведен эксперимент для изучения зависимости времени решения от количества запущенных блоков (в каждом блоке 8 скалярных процессоров). Проводился расчет 100 корней СЛАУ при количестве реализаций случайного процесса 1000000, с различным количеством блоков в конфигурации ядра CUDA Эксперимент был проведен для одной матрицы: fidapm11.

Ошибка решения СЛАУ методом Монте-Карло оценивалась при помощи относительной невязки невязка вектора правой части B , рассчитанная по формуле: .

Результаты эксперимента

Таблица 2. Результаты эксперимента по решению СЛАУ

В таблице 2 символом * обозначено то, что метод не сошелся.

Рис.15. Время решения СЛАУ различных размерностей методом Монте-Карло

Рис.16. Время решения СЛАУ различных размерностей методом GMRES

Рис.17. Время решения СЛАУ различных размерностей методом BICG

Рис. 18. Ускорение

Выводы

Проведя анализ полученных результатов можно сделать следующие выводы:

Зависимость времени решения СЛАУ от ее размерности для метода Монте-Карло линейная, что согласуется с теоретическими основами метода
На графиках, изображенных на рисунках 16 и 17, видна квадратичная зависимость времени решения СЛАУ от ее размерности для методов GMRES и BICG
Для СЛАУ небольших размерностей ( для GMRES , для BICG ) метод Монте-Карло оказывается менее эффективен чем итерационные методы.
Метод Монте-Карло показал более высокую надежность в отличие от методов GMRES , BICG , получив решение системы на всех матрицах

Технико-экономическое обоснование эффективности НИОКР

Введение

Дипломная работа посвящена разработке и экспериментальному исследованию семейства численных методов решения СЛАУ большой размерности методов Монте-Карло.

В основе данных методов лежит получение большого числа реализаций стохастического процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Методы используются во многих областях научной деятельности человека, например при решении задач химии, физики, математики, экономики и др. В рамках дипломной работы было проведено исследование применения метода для решения СЛАУ больших размеров при помощи графического адаптера. Его использование позволяет увеличить быстродействие решения задачи при минимизации затрат на аппаратную поддержку алгоритма. Фактически предложенные алгоритмы позволяют использовать маломощные пользовательские персональные компьютеры для решения серьезных задач.

Организационно-экономическая часть работы посвящена разработке комплекса мероприятий организационноэкономического и финансового планов, которые необходимо выполнить для разработки методов и алгоритмов решения СЛАУ на графических адаптерах компании NVIDIA методом Монте-Карло. Алгоритмы и методы реализуются при помощи технологии компании NVIDIA CUDA . Программное обеспечение, созданное в ходе НИОКР, разработано исключительно в интересах кафедры и не предназначено для последующей продажи или внедрения.

Расчет трудоемкости выполнения НИОКР

Для планирования продолжительности выполнения НИОКР используются расчетные и опытно-статистические нормативы. Однако по значительной части работ такие нормативы отсутствуют. Поэтому для определения продолжительности работ используются две оценки времени, выдаваемые ответственным исполнителем: минимальная и максимальная продолжительность работы. При этом оценки рассматриваются не как обязательство ответственного исполнителя, а как предложение, основанное на опыте, интуиции и на учете факторов, влияющих на продолжительность работы.

Рассмотрим перечень работ по всем этапам НИОКР:

техническое задание (ТЗ) постановка задач проекта, определение основных положений и методик;
эскизное проектирование (ЭП) выбор программных средств создания ПО, разработка принципиальных технических решений, комплексное исследование предметной области, формирование алгоритмов работы ПО;
техническое проектирование (ТП) окончательный выбор технических решений, разработка диаграмм классов ПО;
рабочий проект (РП) — непосредственная разработка алгоритмов и технологий, создание модулей программы;
экспериментальные исследования (ЭИ) подготовка экспериментальной базы, исследования работы алгоритма, эксперименты по автоматизированному аннотированию документов, обобщение и оценка результатов экспериментов.

Рассчитываем ожидаемое время выполнения каждой работы t ож :

t min минимальная продолжительность работы, т.е. время, необходимое для выполнения работы при наиболее благоприятном стечении обстоятельств (час, дни, недели и т.д.);

t max — максимальная продолжительность работы, т.е. время, необходимое для выполнения работы при наиболее неблагоприятном стечении обстоятельств (час, дни, недели и т.д.)

Для определения возможного разброса ожидаемого времени рассчитываем дисперсию (рассеивание) :

Для определения количества исполнителей и построения план-графика выполнения НИОКР необходимо рассчитать продолжительность каждого этапа работы (ТЗ, ТПр, ЭП, ТП, РП, ИОО, ИО, ТД). Требуемое количество исполнителей R по этапам определяется по формуле:

источники:

http://poisk-ru.ru/s12823t3.html

http://5fan.ru/wievjob.php?id=78004

Решение систем линейных уравнений монте карло

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Решение системы линейных уравнений методом Монте-Карло

Источник

Решение линейных алгебраических систем методом Монте-Карло

Оглавление

Введение

Конструкторская часть.

Обзор численных методов решения систем линейных алгебраических уравнений (СЛАУ).

Прямые методы решения СЛАУ

Метод Гаусса

Метод LU разложения

Метод Холецкого (метод квадратного корня)

Итерационные методы решения СЛАУ

Метод простой итерации (метод Якоби)

Метод Зейделя

Метод релаксации

Метод сопряженных градиентов

Метод бисопряженных градиентов

Метод GMRES

Корректность постановки задачи и понятие обусловленности

Экспериментальное исследование устойчивости решения

Вычислительные затраты

Обзор метода Монте-Карло

Идея метода

Случайные числа

Описание метода

Разработка параллельной реализации метода Монте-Карло для решения СЛАУ для архитектуры CUDA

Подход «мастер-рабочий»

Метод с перешагиванием

Разделение последовательностей

Параметризация

Выбор подхода для параллельной реализации

Параллельная реализация метода Монте-Карло

Технологическая часть. Разработка программного обеспечения реализующего метод Монте-Карло для решения СЛАУ

Обзор используемых технологий и программных платформ

Технология NVIDIA CUDA

Библиотека CURAND

Библиотека CUSP

Исследовательская часть. Тестирование параллельной реализации метода Монте-Карло и анализ результатов.

Постановка эксперимента

Обзор использованных матриц

Конфигурация использованного оборудования

Методика проведения экспериментов

Результаты эксперимента

Выводы

Технико-экономическое обоснование эффективности НИОКР

Введение

Расчет трудоемкости выполнения НИОКР

Метод LU разложения