Решение систем линейных уравнений
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
  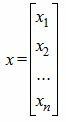 | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда
| A −1 Ax=A −1 b. | (4) |
Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:
| Ex=A −1 b. | (4) |
или, учитывая, что Ex=x:
| x=A −1 b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . . |
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . . |
Вычислим все алгебраические дополнения матрицы A:
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
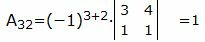 , , |
 . . |
Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
 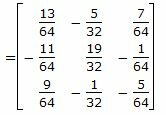 |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными — это система уравнений вида

Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m — уравнений, n — количество неизвестных. x1, x2,…, xn — неизвестные, которые следует определить.
В системе (1) 
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Задача состоит в том, чтобы найти такие 
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент 


Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.
Система линейных уравнений может быть представлена в матричной форме как:
Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:

Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.
Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:

Формально у нас есть еще старое тождество 
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b1:A = A1, b=b1.
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3. N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
где
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5. N, т.е. прибавим к i-ой строке вторую, умноженную на
Здесь
Поступая так и далее, на шаге N -1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы 
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1. N таким образом, чтобы на месте kk оказался элемент 
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:

Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения

эквивалентного начальной системе линейных алгебраических уравнений.
При итерации 

Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при 
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A — квадратная NxN — матрица.
Рассмотрим задачу Ax = b.
Пусть также 
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина 
- если A — диагональная, то
(Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть
вариация правой части, а
соответствующее изменение решения.
Тогда справедливо следующее неравенство:
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
http://matworld.ru/calculator/matrix-method-online.php
http://statistica.ru/branches-maths/chislennye-metody-sistemy-lineynykh-uravneniy/





























 (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть
(Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть  вариация правой части, а
вариация правой части, а  соответствующее изменение решения.
соответствующее изменение решения.



