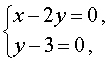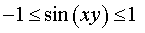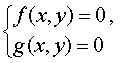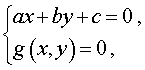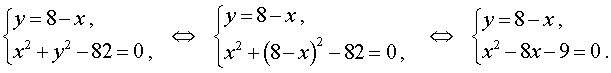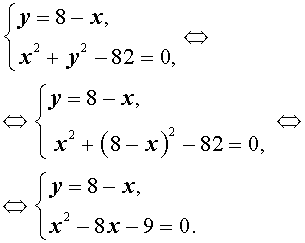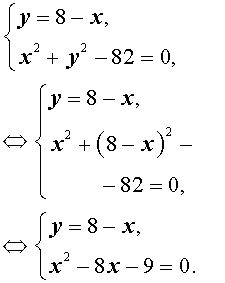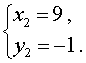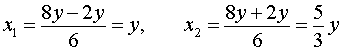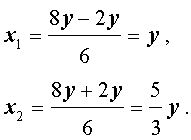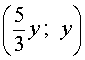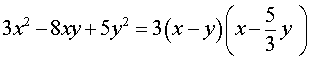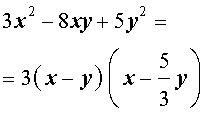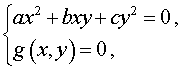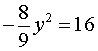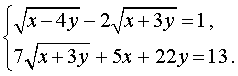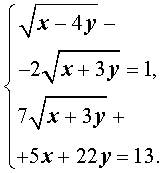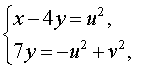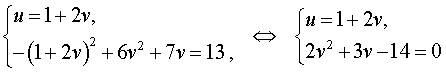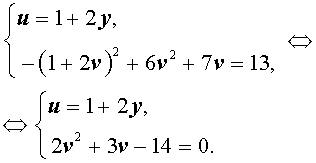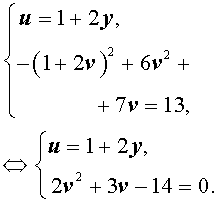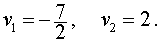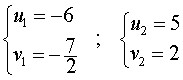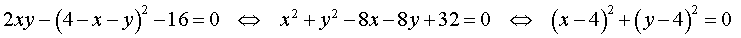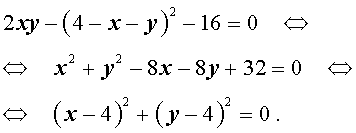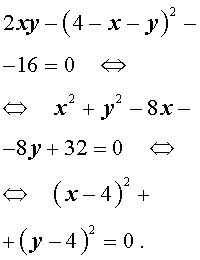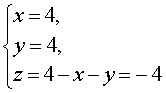Решение систем нелинейных уравнений кратко

Системы с нелинейными уравнениями

Нелинейные уравнения с двумя неизвестными

Системы из двух уравнений, одно из которых линейное

Однородные уравнения второй степени с двумя неизвестными

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Примеры решения систем уравнений других видов

Нелинейные уравнения с двумя неизвестными

Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.

Задание числовой функции z от двух переменных x и y часто обозначают так:

причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .

Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида

где f (x , y) – любая функция, отличная от функции

где a , b , c – заданные числа.

Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.

Пример 1 . Решить уравнение

Решение . Преобразуем левую часть уравнения (3):

Таким образом, уравнение (3) можно переписать в виде

Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений

решением которой служит пара чисел (6 ; 3) .

Пример 2 . Решить уравнение

вытекает, что уравнение (5) решений не имеет.

Ответ : Решений нет.

Пример 3 . Решить уравнение

Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида

где y – любое число.

Системы из двух уравнений, одно из которых линейное

Определение 4 . Решением системы уравнений

называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.

Системы из двух уравнений, одно из которых линейное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 4 . Решить систему уравнений

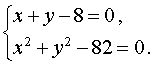(7)

Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:

Таким образом, решениями системы (7) являются две пары чисел

и

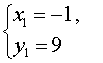
Ответ : (– 1 ; 9) , (9 ; – 1)

Однородные уравнения второй степени с двумя неизвестными

Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида

где a , b , c – заданные числа.

Пример 5 . Решить уравнение

Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле

откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):

Ответ . Решениями уравнения (8) являются все пары чисел вида

( y ; y) или

где y – любое число.

Следствие . Левую часть уравнения (8) можно разложить на множители

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, одно из которых однородное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 6 . Решить систему уравнений

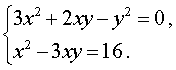(9)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

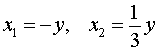
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение

корнями которого служат числа y₁ = 2 , y₂ = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .

,

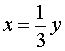
из второго уравнения системы (9) получаем уравнение

которое корней не имеет.

Ответ : (– 2 ; 2) , (2 ; – 2)

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Пример 7 . Решить систему уравнений

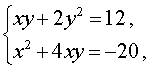(10)

Решение . Совершим над системой (10) следующие преобразования:

• второе уравнение системы оставим без изменений;
• к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).

В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:

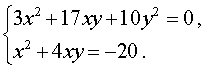(11)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

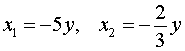
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение

которое корней не имеет.

,

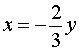
из второго уравнения системы (11) получаем уравнение

,

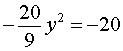
корнями которого служат числа y₁ = 3 , y₂ = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .

Ответ : (– 2 ; 3) , (2 ; – 3)

Примеры решения систем уравнений других видов

Пример 8 . Решить систему уравнений (МФТИ)

Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:

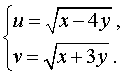(13)

Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что

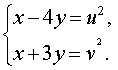(14)

Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (14) преобразуется в равносильную ей систему

из которой находим

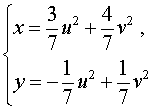(15)

Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде

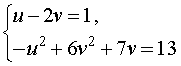(16)

У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:

Следовательно, решениями системы (16) являются две пары чисел

Из формул (13) вытекает, что 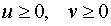, поэтому первое решение должно быть отброшено. В случае u₂ = 5, v₂ = 2 из формул (15) находим значения x и y :

Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.

Пример 9 . Решить систему из двух уравнений с тремя неизвестными

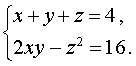(17)

Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:

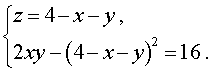(18)

Перепишем второе уравнение системы (18) в другом виде:

Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .

Ответ : (4 ; 4 ; – 4)

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».

Нелинейные уравнения и системы уравнений. Методы их решения.

Нелинейные уравнения и системы уравнений. Методы их решения.

Одной из важных задач прикладной математики является задача решения нелинейных уравнений, встречающихся в разных областях научных исследований.

Под нелинейными уравнениями ( nonlinear equations ) понимаются алгебраические и трансцендентные уравнения с одним неизвестным в следующем виде:

,

где — действительное число, — нелинейная функция.

Под системой нелинейных уравнений понимается система алгебраических и трансцендентных уравнений в следующем виде:

где < > — действительные числа, < … > — нелинейные функции.

Алгебраическое уравнение — это уравнение содержащие только алгебраические функции, которое можно представить многочленом n ‐ ой степени с действительными коэффициентами (целые, рациональные, иррациональные) в следующем виде:

.

Трансцендентное уравнение – это уравнение содержащие в своем составе функции, которые являются не алгебраическими. Простейшими примерами таких функций служат показательная функция, тригонометрическая функция, логарифмическая функция и т.д.

Решением нелинейного уравнения (или системы нелинейных уравнений) называют совокупность (группа) чисел , которые, будучи подставлены на место неизвестных , обращают каждое уравнение (или систему уравнений) в тождество:

.

Для решения нелинейных уравнений (или систем нелинейных уравнений) существует несколько методов решения: графические, аналитические и численные методы.

Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений.

Аналитические методы (или прямые методы) позволяют определить точные значения решения уравнений. Данный метод позволяет записать корни в виде некоторого соотношения (формул). Подобные методы развиты для решения простейших тригонометрических, логарифмических, показательных, а также алгебраических уравнений. Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. В таких случаях обращаются к численным методам, позволяющим получить приближенное значение корня с любой заданной точностью .

Численные методы решения нелинейных уравнений – это итерационный процесс расчета, который состоит в последовательном уточнении начального приближения значений корней уравнения (системы уравнений). При численном подходе задача о решении нелинейных уравнений разбивается на два этапа:

— локализация (отделение) корней

› Под локализацией корней понимается процесс отыскания приближенного значения корня или нахождение таких отрезков, в пределах которых содержится единственное решение

› Под уточнением корней понимается процесс вычисления приближенных значений корней с заданной точностью по любому численному методу решения нелинейных уравнений.

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно. В случае повторения итерационного процесса при изменении стартовых точек отсутствуют гарантии, что найдется новый корень уравнения, так как итерационный процесс может сойтись к найденному корню.

Для поиска других корней используется метод удаления корней. Данный метод основан на принципе создания новой функции путем деление основной функции на найденный корень уравнения:

.

Так, например, если — корень функции то, чтобы произвести удаление найденного корня и поиск оставшихся корней исходной функции необходимо создать функцию . Точка будет являться корнем функции на единицу меньшей кратности, чем , при этом все остальные корни у функций и совпадают с учетом кратности. Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Следует обратить внимание, что когда производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз. Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Локализация корней.

› Локализация корней аналитическим способом

Для отделения корней уравнения необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень. Дополнительным условием, обеспечивающем единственность корня на отрезке является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной . Таким образом, если на отрезке функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.

› Локализация корней табличным способом

Допустим, что все интересующие нас корни уравнения находятся на отрезке . Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи. Будем вычислять значения , начиная с точки , двигаясь вправо с некоторым шагом h . Как только обнаруживается пара соседних значений , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

Надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( ) на границах текущего отрезка функция принимает значения одного знака, то естественно ожидать, что уравнение корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции на отрезке могут оказаться корни уравнения (рис. 1, а). Также несколько корней на отрезке могут оказаться и при выполнении условия (рис. 1, б). Предвидя подобные ситуации, следует выбирать достаточно малые значения h .

Рис. 1. Варианты поведения функции на интервале локализации корня

Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях h , для его реализации целесообразно использовать вычислительные возможности компьютера.

Отделяя, таким образом, корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска ( h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

Уточнение корней.

На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) e . Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину e :

Существует большое количество численных методов решения нелинейных уравнений для уточнения корней, которые условно можно разделить:

› Методы решение уравнений с одним неизвестным. Основными представителями являются:

— метод половинного деления;

— метод простой итерации;

— метод Ньютона для уравнения с одним неизвестным;

Краткие сведения о решении систем нелинейных уравнений

Лекция 9

Нелинейные системы

Краткие сведения о решении систем нелинейных уравнений

Системы нелинейных уравнений могут возникать при интегрировании уравнений движения деформируемых систем, при решении задач оптимизации и во многих других случаях. Наиболее часто количество уравнений в таких системах количество уравнений равно количеству неизвестных. Во всяком случае, это справедливо для большинства задач вычислительной механики.

Общий вид таких систем:

(9.1)

Как обычно запись системы (9.1) можно значительно упростить, введя векторные обозначения. Обозначим ‑ вектор, содержащий неизвестные, а ‑ вектор функций.

Система (9.1) принимает вид

, (9.2)

внешне совпадающий с единственным уравнением с одним неизвестным, методы решения которого были рассмотрены в предыдущих параграфах. Однако обобщение этих методов на многомерный случай представляет существенные трудности.

Начнем, как обычно, с графической иллюстрации (Рис.9.1). Рассмотрим систему двух уравнений с двумя неизвестными:

На рисунке изображены две поверхности, определяемые уравнениями 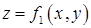и . Очевидно, что уравнения и представляют собой уравнения линий пересечения этих поверхностей с плоскостью . Соответственно точка пересечения этих линий и определяет решение исходной системы.

Попытка обобщить эти наглядные представления на системы с большим количеством уравнений, пожалуй, мало полезна. Хотя в некоторых книгах по численным методам (например, [9.1]) можно встретить формулировку типа: Решение представляет собой точку -мерного пространства, в которой гиперповерхностей пересекаются с гиперплоскостью . Звучит красиво, но, на мой взгляд, наглядностью не отличается.

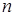
Уже на двумерном случае понятно, что метод половинного деления здесь, к сожалению, не работает. Для одного уравнения этот метод, не отличаясь высокой скоростью, был с другой стороны крайне надежным. Но для одного уравнения в методе бисекций на каждом шаге требовалось вычислить значения функций на границах интервала, то есть всего в двух точках. Уже для двух уравнений аналогичный подход требует определения значений функций на границе двумерной области (пунктирный прямоугольник на рисунке), то есть в бесконечном числе точек.

Более плодотворной выглядит попытка применить идею метода касательных. На рис.9.2 изображены поверхности и . И на этом рисунке видно, что эти две поверхности и плоскость пересекаются в точке, координаты которой и представляют решение системы

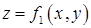
В качестве начального приближения мы принимаем некоторую точку , изображенную на рисунке кружком. На первой поверхности этим значениям аргументов соответствует точка, отмеченная на рисунке крестиком, с координатами . На второй поверхности – точка с координатами . Проведем через точку плоскость касательную к поверхности . На рисунке фрагмент этой плоскости изображен темным треугольником, ограниченным пунктирной линией. Через точку проводим плоскость касательную к поверхности . На рисунке эта плоскость изображена треугольником, ограниченным линиями из точек. Точка , в которой эти плоскости пересекаются между собой и с плоскостью , принимается в качестве очередного приближения. И далее эта процедура повторяется до тех пор, пока не будет достигнута необходимая точность.

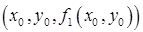
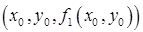
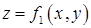
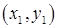
Теперь попробуем перевести эти довольно приблизительные рассуждения перевести на язык формул. Для случая уравнений с неизвестными начальное приближение определяется вектором:

Очередное приближение можно представить как

, или

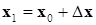
Если разложить функции , определяющие систему (9.1) в ряд Тейлора в окрестности точки (см, например [9.2]), получим следующие выражения:

(9.3)

Производные здесь вычисляются, разумеется, в точке . В методе Ньютона-Рафсона (методе касательных) при определении очередного приближения мы заменяем функции (криволинейные поверхности) их линейными приближениями (касательными плоскостями), то есть в выражениях (9.3) отбрасываем члены второго порядка малости . Полагая значения функций в левой части уравнений (9.3) равными нулю, приходим к системе уравнений

В матричной записи эта система выглядит таким образом:

, (9.4)

,

а матрица

(9.5)

представляет собой хорошо известный по курсу матанализа якобиан.

В случае если якобиан не вырожден , система уравнений (9.4) имеет единственное решение: , и очередное приближение решения имеет вид: . Таким образом, итерационная формула метода Ньютона-Рафсона для системы линейных уравнений имеет вид:

(9.6)

Если рассматривать якобиан как обобщение производной, то можно сказать, что формулы этого метода для системы уравнений и для одного уравнения совпадают.

При программной реализации обычно не вычисляют матрицу обратную якобиану непосредственно, а сначала вычисляют поправку, решая систему

, (9.7)

и затем определяют очередное приближение:

. (9.8)

Объем вычислений для систем, естественно, значительно больше, чем для одного уравнения и, к сожалению, не всегда сходится к решению. В программном комплексе MATLAB для решения систем уравнений можно использовать функцию fsolve (содержится в Optimization Toolbox). Если вы поэкспериментируете с этой функцией, то обнаружите, что не так уж редко функция будет сообщать либо о том, что сходимости добиться не удалось, либо о том, что процесс сходится к некоторой точке, но эта точка не является нулем функций системы.

Вообще проблема решения систем нелинейных уравнений вида еще далека от своего окончательного решения. Не случайно, поэтому, хорошие программы предусматривают возможность неудачи и сообщают о ее причинах.

Что касается метода Ньютона-Рафсона, определяемого формулой (9.6), то он, обладает квадратичной сходимостью, превосходя по эффективности другие методы. Однако для его успешной работы необходимо выполнение следующих условий:

· Якобиан должен быть достаточно хорошо обусловленной матрицей. Иначе будет затруднительно вычислить поправку с хорошей точностью.

· Начальное приближение должно быть достаточно хорошим. Иначе первая же поправка, определяемая по формуле (9.7) может дать не приближение к решению, а удаление от него.

В формулировке обоих этих условий присутствует слово достаточно, не отличающееся здесь математической точностью. И действительно, чаще всего, определить ‑ достаточно ли хорошо выбрано начальное приближение можно только предприняв попытку решения.

Поэтому, как правило, метод Ньютона-Рафсона используют в комбинации с другими методами и применяя различные меры предосторожности. Здесь приведем, предложенную в книге [9.3] стратегию решения ‑ относительно простую, но достаточно надежную. Она основана на ограничении величины поправки (уравнения (9.7) и (9.8)) и требовании уменьшения величин функций с каждой поправкой.

1) Вводится ограничение на величину поправки , где ‑ заданный допуск.

2) Если ‑ останов.

3) Вычислить . Здесь используется не формула (9.7) , но решается задача оптимизации (минимизации): определить , обеспечивающее минимум функции при условии . (Здесь должны использоваться специальные методы оптимизации, не рассматриваемые в данном курсе. Ознакомиться с ними можно по упомянутой книге Каханера, Моулера, Нэша)

4) Если , то шаг принимается как удачный, полагается и . Управление возвращается на второй шаг алгоритма.

5) Иначе полагаем . Управление передается на третий шаг алгоритма

Возможно также обобщение метода секущих на многомерный случай. На рис.9.3 приведена соответствующая иллюстрация для системы двух уравнений. В этом случае для первого приближения надо выбрать три начальных точки , , . На каждой из поверхностей (на рисунке показана только одна из этих поверхностей) этим точкам соответствуют три точки 3-х мерного пространства: , , . Через эти три точки можно провести секущую плоскость. На рисунке эта плоскость изображена затемненным треугольником. Пересечение двух таких плоскостей с плоскостью дает точку , которая считается новым приближением. Для следующей итерации одна из ранее выбранных точек 0,1,2 заменяется на новую 3-ю точку.

В случае системы уравнений для проведения гиперплоскости в -мерном пространстве требуется задать точку. В остальном последовательность действий остается такой же.

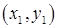
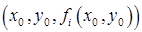
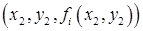
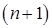
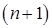
Существует много разновидностей метода секущих, использующий различные способы выбора точек и различные стратегии решения. Ознакомиться с ними можно по книге Ортеги, Рейнболдта [9.1]. Здесь же отметим только, что метод секущих и в многомерном случае можно рассматривать как вариант метода Ньютона-Рафсона с заменой производных их приближенными выражениями через значения функций в отдельных точках (разностными соотношениями).

Вопрос о сходимости методов здесь рассмотрим на примере метода простой итерации. Так же как и в случае одной функции можно ввести понятия неподвижной точки и сжимающего отображения

Рассмотрим некоторую -мерную вектор-функцию от переменных. Здесь . Эту функцию можно рассматривать как оператор, отображающий точки -мерного пространства на то же самое пространство.

Определение 1. Точка для которой называется неподвижной точкой оператора (функции) .

Определение 2. Оператор (функция) называется сжимающим оператором на некотором множестве , если для любых значений и , принадлежащих этому множеству , выполняется неравенство

, (9.9)

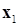
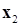
где называется коэффициентом сжатия.

Для исследования сходимости итерационных методов принципиальное значение имеет следующая теорема:

Принцип сжимающих отображений. Пусть оператор определен на множестве , представляющем собой окрестность некоторой точки : и является на этом множестве сжимающим оператором с коэффициентом сжатия , причем

.

Тогда итерационный метод сходится к неподвижной точке оператора при любом начальном приближении .

Доказательства этой теоремы здесь не приводится. Более подробную информацию по этому вопросу можно найти в книгах [9.1, 9.4].

Отметим, что, как и в случае одного уравнения, вместо условия (9.9) можно, с некоторыми оговорками, воспользоваться более строгим условием:

для (9.10)

(норма якобиана функции меньше единицы).

Сформулированный выше принцип сжимающих отображений применим для исследования сходимости только таких итерационных методов, которые являются разновидностями метода простой итерации. То есть метода, который исходную систему уравнений

заменяет эквивалентной системой вида

и определяет итерационную последовательность как

Метод Ньютона-Рафсона удовлетворяет этому описанию, если положить . Метод секущих, в котором для получения очередного приближения используются уже не одна, а несколько точек, уже не является методом простой итерации. И исследование сходимости здесь представляет большие сложности.

Литература

9.1. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.: Мир, 1975. – 558 с.

9.2. Смирнов В.И. Курс высшей математики. Том I. – М.: Наука, 1967. – 480 с.

9.3. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение. – М.: Мир, 1998. – 575 с.

9.4. Самарский А.А., Гулин А.В. Численные методы. ‑ М.: Наука, 1989. – 432 с.