Решение систем тригонометрических уравнений решение тригонометрических неравенств

Е.П. Нелин, В.А. Лазарев

АЛГЕБРА

и начала математического

анализа

10 класс

учреждений. Базовый и

§ 21. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Работу выполнила: Мусина В.А. студентка группы 45.3

Системы тригонометрических уравнений решаются с помощью тех же методов, что и алгебраические системы, в частности это исключение неизвестных и замена переменных. Исключить неизвестные можно с помощью одного из двух приемов:из одного уравнения выразить какое-то неизвестное (или функцию от него) и подставить его в другие или преобразовать данные уравнения и потом составить из них комбинации, в которых число неизвестных уменьшается.

Задача 1 . Решите систему уравнений

Из первого уравнения находим и подставляем во второе.

Получаем

Замечание. Если бы для нахождения значения y мы не рассмотрели отдельно формулу (1) со знаком «+» и знаком «–», то вместе с верными решениями получили бы и посторонние решения заданной системы.

Действительно, в таком случае имеем

Тогда, например, при n = 0 получаем

Таким образом, кроме решений, которые вошли в ответ, мы имеем еще две возможности:

Но эти пары значений х и у не являются решениями заданной системы, поскольку они не удовлетворяют первому уравнению.

Поэтому следует запомнить:

Когда решение уравнения cos x = а приходится применять для дальнейших преобразований, то удобно записывать его в виде двух формул: отдельно со знаком «+» и отдельно со знаком «–».

Задача 2 . Решите систему уравнений

Почленно сложим и вычтем эти уравнения. Получим равносильну систему

Представим последнюю систему в виде совокупности двух систем, записывая решения второго уравнения отдельно со знаком «+» и отдельно со знаком «–»:

Почленно складывая и вычитая уравнения этих систем, находим x и y:

Замечание. В запись ответа вошли два параметра n и k, которые независимо друг от друга «пробегают» множество целых чисел. Если попробовать при решении заданной системы воспользоваться только одним параметром, например n, то это приведет к потере решений. Таким образом, в каждом случае, когда система тригонометрических уравнений приводится к системе, состоящей из элементарных тригонометрических уравнений (то есть из уравнений вида sin x = a, cos x = a, tg x = a, ctg x = a), при решении каждого из этих уравнений необходимо использовать свой целочисленный параметр.

Вопросы для контроля

1. Какие методы используются для решения систем тригонометрических уравнений?
2. Объясните, в каком случае при формальном решении системы уравнений мы можем потерять часть решений, а в каком случае —получить посторонние решения. Решите эту систему.

Упражнения

Решите систему уравнений (1–8).

Решение тригонометрических неравенств и систем

п.1. Примеры

Пример 1. Решите неравенства:
a) \(ctg\left(\frac<3\pi><2>+\frac x3\right)-\frac<1><\sqrt<3>>\leq 0\)
По формуле приведения \(ctg\left(\frac<3\pi><2>+\frac x3\right)=-tg\frac x3\)
Получаем:
\(-tg\frac x3-\frac<1><\sqrt<3>>\leq 0\Rightarrow tg\frac x3\geq \frac<1><\sqrt<3>>\)
\(arctg\frac<1><\sqrt<3>>+\pi k\leq\frac x3\lt\frac\pi2+\pi k\)
\(3\cdot\frac\pi6+3\pi k\leq x\lt\frac<3\pi><2>+3\pi k\)
\(\frac\pi2+3\pi k\leq x\lt\frac<3\pi><2>+3\pi k\)

Ответ: \(\left.\left[\frac\pi2+3\pi k;\ \frac<3\pi><2>+3\pi k\right.\right) \)

б) \(tg\left(2x+\frac\pi4\right)+1\geq 0\)
\(tg\left(2x+\frac\pi4\right)\geq -1\)
\(-\frac\pi4+\pi k\leq 2x+\frac\pi4\lt\frac\pi2+\pi k\)
\(-\frac\pi2+\pi k\leq 2x\lt\frac\pi4+\pi k\)
\(-\frac\pi4+\frac<\pi k><2>\leq x\lt\frac\pi8+\frac<\pi k><2>\)
Ответ: \(\left.\left[-\frac\pi4+\frac<\pi k><2>;\ \frac\pi8+\frac<\pi k><2>\right.\right) \)

в) \(3cos2x\leq 1\) \begin cos2x\leq\frac13\\ arccos\frac13+2\pi k\leq 2x\leq 2\pi-arccos\frac13+2\pi k\\ \frac12 arccos\frac13+\pi k\leq x\leq \pi-\frac12 arccos\frac13+\pi k \end Ответ: \(\left[ \frac12 arccos\frac13+\pi k;\ \pi-\frac12 arccos\frac13+\pi k\right] \)

г) \(cos^2x-2cosx\gt 0\)
\(cosx(cosx-2)\gt 0\)
\(cosx-2\lt 0\) при любом \(x\). Делим неравенство на отрицательную скобку, получаем:
\(cosx\lt 0\)
\(\frac\pi2+2\pi k\lt x\lt\frac<3\pi><2>+2\pi k\)
Ответ: \(\left(\frac\pi2+2\pi k;\ \frac<3\pi><2>+2\pi k\right) \)

Пример 2*. Решите неравенства:

a) \(\frac12\lt sinx\leq \frac<\sqrt<2>><2>\)

Ответ: $$ \left.\left(\frac\pi6+2\pi k;\ \frac\pi4+2\pi k\right.\right]\cup \left.\left[\frac<3\pi><4>+2\pi k;\ \frac<5\pi><6>+2\pi k\right.\right) $$б) \(sin2x+\sqrt<3>cos2x\geq 1\)
Вводим вспомогательный угол, умножаем на \(\frac12\) \begin \frac12 sin2x+\frac<\sqrt<3>><2>cos2x\geq\frac12\\ sin\frac\pi6 sin2x+cos\frac\pi6 cos2x\geq\frac12\\ cos\left(2x-\frac\pi6\right)\geq\frac12\\ -\frac<\pi><3>+2\pi k\leq 2x-\frac\pi6\leq \frac\pi3+2\pi k\\ -\frac\pi6+2\pi k\leq 2x\leq \frac\pi2+2\pi k\\ -\frac<\pi><12>+\pi k\leq x \leq \frac\pi4+\pi k \end Ответ: $$ \left[-\frac<\pi><12>+\pi k;\ \frac\pi4+\pi k\right] $$

в) \(tg^2x-\left(1+\sqrt<3>\right)tg x+\sqrt<3>\lt 0\)
\(tg^2x-tgx-\sqrt<3>tgx+\sqrt<3>\lt 0\)
\(tgx(tgx-1)-\sqrt<3>(tgx-1)\lt 0\)
\((tgx-\sqrt<3>)(tgx-1)\lt 0\)
\(1\lt tgx\lt \sqrt<3>\)
\(arctg1+\pi k\lt x\lt arctg\sqrt<3>+\pi k\)
\(\frac\pi4+\pi k\lt x\lt\frac\pi6+\pi k\)
Ответ: \(\left(\frac\pi4+\pi k;\ \frac\pi6+\pi k\right)\)

г) \(\sqrt<5-2sinx>\geq 6sinx-1\)
Замена: \(t=sinx,\ -1\leq t\leq 1\)
Методы решения иррациональных неравенств – см. §11 справочника для 9 класса. \begin \begin \sqrt<5-2t>\geq 6t-1\\ -1\leq t\leq 1 \end \Rightarrow \begin \left[ \begin \begin 6t-1\lt 0\\ 5-2t\geq 0 \end \\ \begin 6t-1\geq 0\\ 5-2t\geq (6t-1)^2 \end \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \begin \left[ \begin \begin t\lt\frac16\\ t\leq\frac52 \end \\ \begin t\geq\frac16\\ 5-2t\geq 36t^2-12t+1 \end \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \\ \Rightarrow \begin \left[ \begin t\lt\frac16 \\ \begin t\geq\frac16\\ 18t^2-5t-2\leq 0 \end \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \begin \left[ \begin t\lt\frac16 \\ \begin t\geq\frac16\\ (9t+2)(2t-1)\leq 0 \end \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \begin \left[ \begin t\lt\frac16 \\ \begin t\geq\frac16\\ -\frac29\leq t\leq \frac12 \end \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \\ \Rightarrow \begin \left[ \begin t\lt\frac16 \\ \frac16\leq t\leq\frac12 \end \right. \\ -1\leq t\leq 1 \end \Rightarrow \begin t\leq\frac12 \\ -1\leq t\leq 1 \end \Rightarrow -1\leq t\leq\frac12 \end Возвращаемся к исходной переменной: $$ -1\leq sinx\leq\frac12 \Rightarrow sinx\leq\frac12\Rightarrow -\frac<7\pi><6>+2\pi k\leq x\leq \frac\pi6+2\pi k $$
Ответ: \(\left[-\frac<7\pi><6>+2\pi k;\ \frac\pi6+2\pi k\right]\)

Пример 3*. Решите системы:
a) \begin \begin sin^2x+sin^2x=sin^2 3x\\ cosx\lt-\frac12 \end \end Решаем уравнение: \begin sin^2 2x=sin^2 3x-sin^2x=(sin3x+sinx)(sin3x-sinx)\\ sin^22x=2sin2xcosx\cdot 2sinxcos2x=sin2x\cdot(2sinxcosx)\cdot 2cos2x\\ sin^22x=sin^22x\cdot 2cos2x\\ sin^22x(1-2cos2x)=0\\ \left[ \begin sin^22x=0\\ 1-2cos2x=0 \end \right. \Rightarrow \left[ \begin \frac<1-cos4x><2>=0\\ cos2x=\frac12 \end \right. \Rightarrow \left[ \begin cos4x=1\\ 2x=\pm\frac\pi3+2\pi k \end \right. \Rightarrow \left[ \begin 4x=2\pi k\\ x=\pm\frac\pi6+\pi k \end \right. \Rightarrow\\ \Rightarrow \left[ \begin x=\frac<\pi k> <2>\\ x=\pm\frac\pi6+\pi k \end \right. \end

Отмечаем полученные решения на числовой окружности, задаем дугу \(cosx\lt-\frac12\), отбираем решения, попавшие на дугу.

Получаем три базовых точки \(\pm\frac<5\pi><6>,\pi\).
С учетом полного периода 2πk записываем всё множество решений.

б) \begin \begin 2sin^2x-sinx+sin3x\lt 1\\ cosx\gt 0 \end \end Разность синусов: \(sin⁡3x-sin⁡x=2sin⁡xcos⁡2x\)
В первом неравенстве получаем: \begin 2sin^2x+2sinxcos2x\lt 1\\ 2sinxcos2x\lt 1-2sin^2x\\ 2sinxcos2x\lt cos2x\\ cos2x(2sinx-1)\lt 1\\ \left[ \begin \begin cos2x\gt 0\\ 2sinx-1\lt 0 \end \\ \begin cos2x\lt 0\\ 2sinx-1\gt 0 \end \end \right. \Rightarrow \left[ \begin \begin -\frac\pi2+2\pi k\lt 2x\lt\frac\pi2+2\pi k\\ sinx\lt\frac12 \end \\ \begin \frac\pi2+2\pi k\lt 2x\lt\frac<3\pi><2>+2\pi k\\ sinx\gt\frac12 \end \end \right. \Rightarrow \left[ \begin \begin -\frac\pi4+\pi k\lt x\lt\frac\pi4+\pi k\\ sinx\lt\frac12 \end \\ \begin \frac\pi4+\pi k\lt x\lt\frac<3\pi><4>+\pi k\\ sinx\gt\frac12 \end \end \right. \end

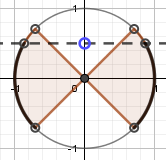$$ \begin \frac\pi4+\pi k\lt x\lt\frac<\pi><4>+\pi k\\ sinx\lt\frac12 \end $$ $$ \left(-\frac\pi4;\ \frac\pi6\right)\cup \left(\frac<5\pi><6>;\ \frac<5\pi><4>\right) $$ С полным периодом \(2\pi k\)

$$ \begin \frac\pi4+\pi k\lt x\lt\frac<3\pi><4>+\pi k\\ sinx\gt\frac12 \end $$ $$ \left(\frac\pi4;\ \frac<3\pi><4>\right) $$ С полным периодом \(2\pi k\)

Учитываем второе неравенство, \(cosx\gt 0\). Отбираем только решения справа от оси \(Y\).
Получаем: \(\left(-\frac\pi4;\frac\pi6\right)\cup\left(\frac\pi4;\frac\pi2\right)\)
Ответ: \(\left(-\frac\pi4+2\pi k;\ \frac\pi6+2\pi k\right)\cup \left(\frac\pi4+2\pi k;\ \frac\pi2+2\pi k\right)\)

Системы тригонометрических неравенств и методы их решения

Системы неравенств можно решать с помощью единичной окружности, придерживаясь следующего алгоритма:

1. Отметить на окружности решение первого неравенства.
2. Отметить решение второго неравенства.
3. Выделить общее решение (пересечение дуг).
4. Записать общее решение системы неравенств с учетом периода.

Пример 1. Ре­шите си­сте­му нера­венств: \(\begin sinx>-\frac<\sqrt2>2, \\ cosx\le\frac<\sqrt3>2. \\ \end\)

Решение: Решим про­стей­шие нера­вен­ства с по­мо­щью фор­мул общих ре­ше­ний: \(x\in (arcsina+2\pi n; \pi-arcsina+2\pi n), n\in Z \ и \\ x\in[arccosa+2\pi n; 2\pi-arccosa+2\pi n], n\in Z.\)

Для наших нера­венств имеем два про­ме­жут­ка ре­ше­ний:

\(1)\ x\in (arcsin(-\frac<\sqrt2>2)+2\pi n; \pi-arcsin(-\frac<\sqrt2>2)+2\pi n), n\in Z \Rightarrow \\ x\in(-\frac<\pi>4+2\pi n; \pi+\frac<\pi>4+2\pi n) \Rightarrow x\in(-\frac<\pi>4+2\pi n; \frac<5\pi>4+2\pi n), n\in Z. \)

\(2)\ x\in [arccos\frac<\sqrt3>2+2\pi n; 2\pi-arccos\frac<\sqrt3>2+2\pi n], n\in Z \Rightarrow \\x\in[\frac<\pi>6+2\pi n; 2\pi-\frac<\pi>6+2\pi n] \Rightarrow x\in[\frac<\pi>6+2\pi n; \frac<11\pi>6+2\pi n], n\in Z.\)

Для этих двух про­ме­жут­ков необ­хо­ди­мо ука­зать пе­ре­се­че­ние. Изоб­ра­зим это на три­го­но­мет­ри­че­ской окруж­но­сти:

Видно, что пе­ре­се­че­ни­ем об­ла­стей ре­ше­ний яв­ля­ет­ся про­ме­жу­ток:

\(x\in[\frac<\pi>6+2\pi n; \frac<5\pi>4+2\pi n), n\in Z\) .

Про­ме­жу­ток \(x\in(-\frac<\pi>4+2\pi n; \frac<11\pi>6+2\pi n], n\in Z\) не яв­ля­ет­ся ча­стью ре­ше­ния, т. к. на самом деле здесь об­ла­сти не пе­ре­се­ка­ют­ся, по­сколь­ку лежат в раз­ных диа­па­зо­нах углов: от­ри­ца­тель­ном и по­ло­жи­тель­ном.

Об­ра­ти­те вни­ма­ние на то, что на­ча­ло про­ме­жут­ка ре­ше­ний вклю­ча­ет­ся, а конец ис­клю­ча­ет­ся.

Ответ: \(x\in[\frac<\pi>6+2\pi n; \frac<5\pi>4+2\pi n), n\in Z\) .