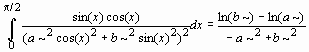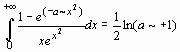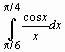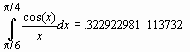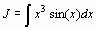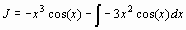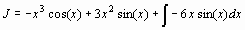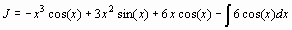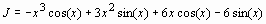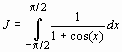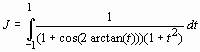Решение систем уравнений с интегралами maple
Аналитическое и численное интегрирование.
Неопределенный интеграл 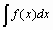
прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования;
отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int . Команда Int выдает на экран интеграл в аналитическом виде математической формулы.
Для вычисления определенного интеграла 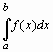
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous) , то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity.
Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e) , где e – точность вычислений (число знаков после запятой).
Интегралы, зависящие от параметра. Ограничения для параметров.
Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо других ограничений. Рассмотрим в качестве примера интеграл 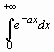
Definite integration: Can’t determine if the integral is convergent.
Need to know the sign of —> a
Will now try indefinite integration and then take limits.
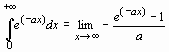
Таким способом интеграл с параметром не вычислить. Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи команды assume(expr1) , где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2) , где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.
После наложения ограничений на параметр Maple добавляет к его имени символ (
), например параметр a , на который были наложены некоторые ограничения, в сроке вывода будет иметь вид: a
Описание наложенных ограничений параметра a можно вызвать командой about(a) . Пример: наложить ограничения на параметр a такие, что a > — 1, a £ 3:
> assume(a>-1); additionally(a about(a);
Originally a, renamed a
is assumed to be: RealRange(Open(-1),3)
Вернемся к вычислению интеграла с параметром 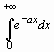
Обучение основным методам интегрирования.
В Maple имеется пакет student , предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. К таким командам относятся интегрирование по частям inparts и замена переменной changevar .
Формула интегрирования по частям:
Если обозначить подынтегральную функцию f=u ( x ) v’ ( x ), то параметры команды интегрирования по частям такие: intparts(Int(f, x), u), где u – именно та функция u(x) , производную от которой предстоит вычислить по формуле интегрирования по частям.
Если в интеграле требуется сделать замену переменных x=g ( t ) или t=h ( x ), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x), t), где t — новая переменная.
Обе команды intparts и changevar не вычисляют окончательно интеграл, а лишь производят промежуточную выкладку. Для того, чтобы получить окончательный ответ, следует, после выполнения этих команд ввести команду value(%); где % — обозначают предыдущую строку.
Не забудьте, перед использованием описанных здесь команд обязательно загрузить пакет student командой with(student).
Задание 4.
- Найти неопределенные интегралы: а)
;
б) 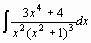
Найти определенный интеграл 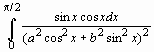
> assume (a>0); assume (b>0);
Найти несобственный интеграл 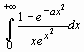
Численно найти интеграл
Полностью проделать все этапы вычисления интеграла 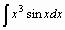
> restart; with(student): J=Int(x^3*sin(x),x);
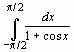 с помощью универсальной подстановки
с помощью универсальной подстановки 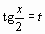 .
.Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение уравнений
Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений
Системы уравнений
Maple может решать системы линейных и нелинейных уравнений, но это хитрое дело, поскольку, чтобы разобраться в происходящем, надо рисовать уравнения, а это сложнее, так как пространство решений – многомерное.
Применяются команды solve и fsolve , но в этом случае им задаются наборы (в фигурных скобках) уравнений и переменных.
В первом примере используем solve для простой задачи линейной алгебры: John вдвое старше Kimberly. Возраст Kimberly плюс возраст John равен 27. Найти возраст каждого. Если использовать пакет LinearAlgebra, то придется рассматривать матрицу, но можно применить solve (и fsolve ), которые могут непосредственно работать с уравнениями:
Поскольку не надо беспокоиться о переводе в матричный вид, то получился иной метод решения систем линейных уравнений.
solve и fsolve можно применять для решения нелинейных систем, т. е. систем уравнений, в которых переменные – квадраты, кубы, синусы, экспоненты и т. п. Например, вот система двух нелинейных уравнений:
Вначале попробуем применить команду solve :
Maple сделал по-умному: чтобы получить уравнение для х , он исключил у из Е2 с помощью Е1 . Затем он факторизовал это квадратное уравнение, выдал ответ (x,y)=(3,4) и свел оставшуюся часть задачи к кубической. Если завершить задачу командой evalf , получим:
Но если нарисовать кубическую часть в RootOf (для оценки положения корней), то увидите, что есть еще два решения. Где же они? Примените fsolve и получите:
что еще хуже, так как дает один корень. Для поиска корней можно задавать примерно правильные числа в качестве подсказок для fsolve :
Простой способ заставить Maple дать все 4 корня: повторяйте процедуру, заменяя все целые числа на числа с плавающей точкой:
Будьте изобретательны
и пробуйте разные пути решения задачи,
возможно, один сработает.
В Maple есть другой полезный инструмент для случая двух нелинейных уравнений с двумя неизвестными. Точно так же, как в задачах с одной переменной, полезно сначала строить график, чтобы увидеть, где есть решения. В данном случае двумерные графики помогут искать корни двух неизвестных величин. Примените команду построения графиков implicitplot , которая берет уравнение с двумя переменными, вроде x 2 – y = 5, и строит определяющую их кривую в плоскости xy (для добавления команды графики надо вначале загрузить пакет графики with(plots) ):
Для графического поиска решений постройте оба уравнения на одном графике и посмотрите, где две кривые пересекают друг друга.
Из картинки ясно, что две параболы пересекаются в четырех местах, поэтому должно быть четыре решения. Окно графика должно быть достаточным, чтобы увидеть всю картинку. А если оно мало, то получится вот что:
Если у вас есть три нелинейных уравнения с тремя переменными, implicitplot3d может сделать нечто подобное (см. Maple help).
Найдите все решения (Re и Im) системы уравнений
Чтобы определить количество искомых корней, сначала постройте график с помощью implicitplot .
Вот еще нелинейная система:
Вначале попробуем solve :
(Maple на мгновение задумается, но ничего не произойдет.) Теперь попробуем fsolve с диапазонами для каждой переменной:
Похоже, что (x, y, z) = (1, 1, 3) достаточно близко к решению. Предупреждение: в трех и более измерениях Maple может ошибиться и работать, несмотря на то, что:
(a) известно, что здесь есть решение и
(b) указано, где искать приближенное значение корня.
Для лучшего понимания, где следует искать решение, можно применить implicitplot3d :
Щелкните на рисунке и покрутите его, чтобы разглядеть подробнее. После этого перерисуйте график так, чтобы он был вблизи известного решения: [x, y, z]=[1, 1, 3]:
В середине графика все три поверхности – E1 , E2 и E3 – пересекаются в точке. Это и есть то, что искали с помощью implicitplot3d , но в целом рассматривать трехмерные задачи сложно.
Пусть гладкая функция y(x) представлена тремя точками (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ). Предположим, что эти точки определяют параболу вида y(x) = a + bx + cx 2 и что есть три аппроксимирующих уравнения для нахождения коэффициентов параболы a, b, c. Постройте эти три уравнения и используйте solve , чтобы найти формулы для a, b, c, а затем определите выражение Maple для параболы.
Задание выглядит вполне приемлемо для равноотстоящих точек. Пусть x 2 = x 1 + h и x 3 = x 1 + 2h . Упростим выражения для a, b, c. В результате получили приближенную форму функции, с которой можно работать:
(a) Оцените площадь под кривой между x 1 и x 3 путем интегрирования параболы между этими двумя пределами. Получится правило Симпсона. Чтобы посмотреть, хорош ли этот приближенный интеграл, задайте x 1 = 0, x 2 = 0.5, x 3 = 1.0 и y 1 = cos(x 1 ), y 2 = cos(x 2 ), y 3 = cos(x 3 ) , при этом приближенное значение площади будет близко к 
(b) Оцените производную функции у(х) в средней точке х 2 путем дифференцирования параболы и вычисления значения производной в x = x 2 . Она называется формулой центральных разностей для первой производной. Проверьте ее точность при x 2 = 0.5, используя x 1 = 0.4 и x 3 = 0.6 с функцией
(c) Повторно дифференцируя формулу параболы, оцените вторую производную функции у(х) в x 2 . Это центральная вторая производная для равноотстоящих точек. Проверьте ее точность, как в части (b).
Эти формулы дифференцирования и интегрирования понадобятся в курсе физики.
Решение систем уравнений с интегралами maple
прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования;
отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int. Команда Int выдает на экран интеграл в аналитическом виде математической формулы.
Для вычисления определенного интеграла
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity.
Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой).
Интегралы, зависящие от параметра. Ограничения для параметров.
Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо других ограничений. Рассмотрим в качестве примера интеграл
> Int ( exp (- a * x ), x =0..+ infinity )=
Definite integration: Can’t determine if the integral is convergent.
Need to know the sign of —> a
Will now try indefinite integration and then take limits.
Таким способом интеграл с параметром не вычислить. Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.
После наложения ограничений на параметр Maple добавляет к его имени символ (
), например параметр a, на который были наложены некоторые ограничения, в сроке вывода будет иметь вид: a
Описание наложенных ограничений параметра a можно вызвать командой about(a). Пример: наложить ограничения на параметр a такие, что a>-1, a £ 3:
Originally a, renamed a
is assumed to be: RealRange(Open(-1),3)
Вернемся к вычислению интеграла с параметром
Обучение основным методам интегрирования.
В Maple имеется пакет student, предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. К таким командам относятся интегрирование по частям inparts и замена переменной changevar.
Формула интегрирования по частям:
Если обозначить подынтегральную функцию f=u(x)v’(x), то параметры команды интегрирования по частям такие: intparts(Int(f, x), u), где u – именно та функция u(x), производную от которой предстоит вычислить по формуле интегрирования по частям.
Если в интеграле требуется сделать замену переменных x=g(t) или t=h(x), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x), t), где t — новая переменная.
Обе команды intparts и changevar не вычисляют окончательно интеграл, а лишь производят промежуточную выкладку. Для того, чтобы получить окончательный ответ, следует, после выполнения этих команд ввести команду value(%); где % — обозначают предыдущую строку.
Не забудьте, перед использованием описанных здесь команд обязательно загрузить пакет student командой with(student).
http://mmlab2.uginfo.sfedu.ru/chapters/ch6/chapter6_2.html
http://www.sites.google.com/site/camoucitelmaple13/urok-5-integrirovanie-5-1-analiticeskoe-i-cislennoe-integrirovanie

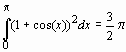
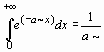
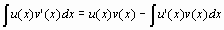
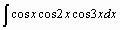 ;
;