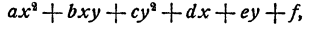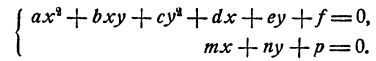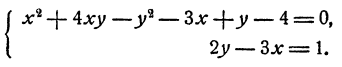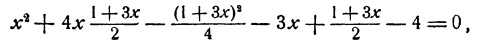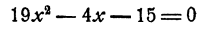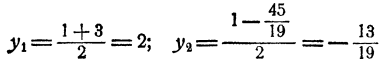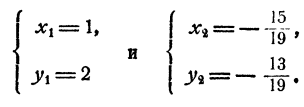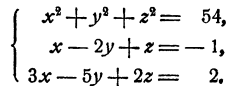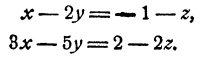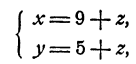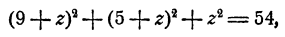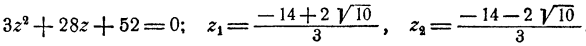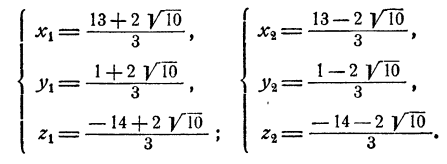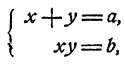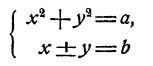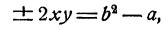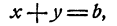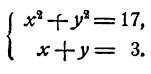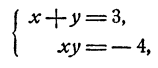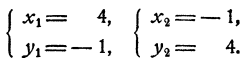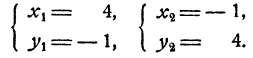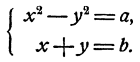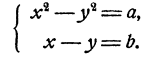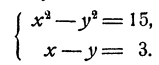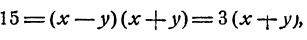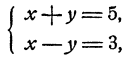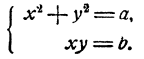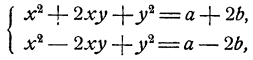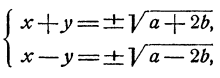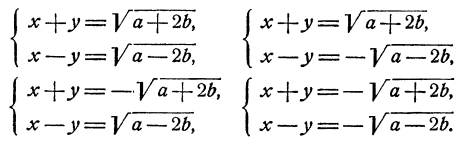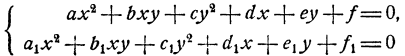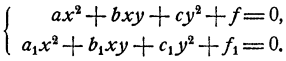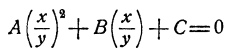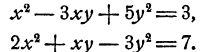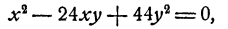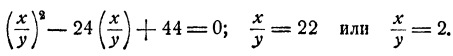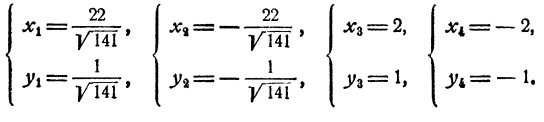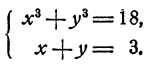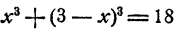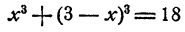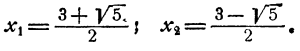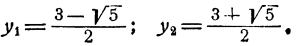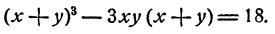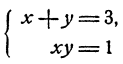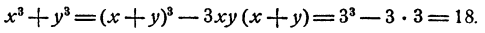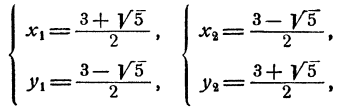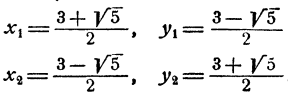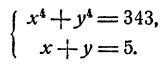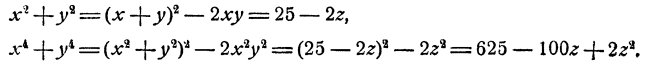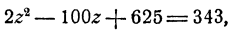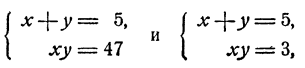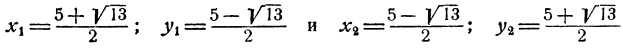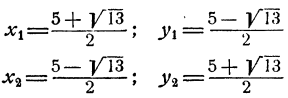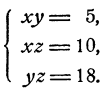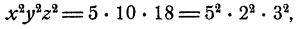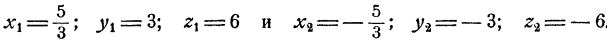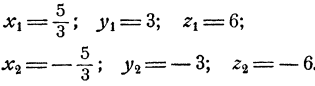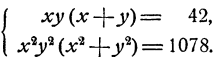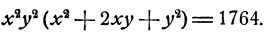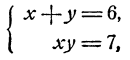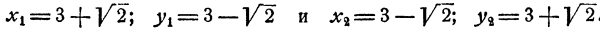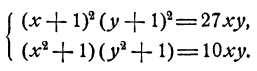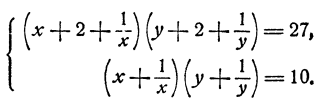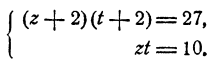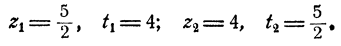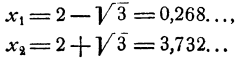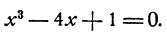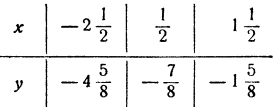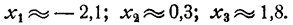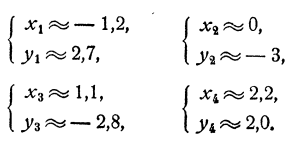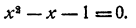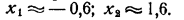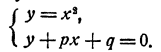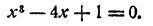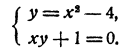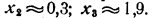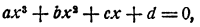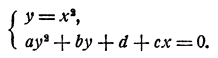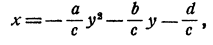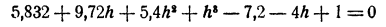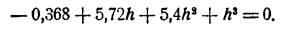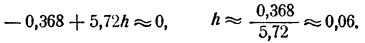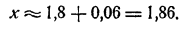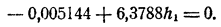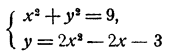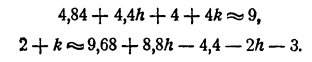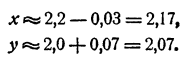Системы уравнений высших степеней в математике с примерами решения и образцами выполнения
Системы двух уравнений первой и второй степени с двумя неизвестными:
Общий вид многочлена второй степени от двух переменных у и x, очевидно, следующий:
где а, b, с, d, е, f—данные числа. Общий вид системы уравнений с двумя неизвестными, состоящей из одного уравнения первой степени и одного уравнения второй степени, следующий:
Система такого вида легко решается способом подстановки. Именно, из второго уравнения можно выразить одно из неизвестных через другое и затем подставить в первое уравнение. В результате этого первое уравнение превратится в уравнение с одним неизвестным, вообще говоря, квадратное. Решив это уравнение, мы сможем определить затем и значения нового неизвестного.
При этом способе решения систем проверка полученных решений посредством подстановки в уравнение системы не обязательна и производится только для контроля правильности вычислений, ибо можно доказать, что при исключении одного неизвестного указанным способом лишних решений возникнуть не может.
Пример:
Решение:
Исключим из системы неизвестное у. С этой целью решим второе уравнение относительно у. Получим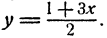 
Затем подставим найденное выражение для у в первое уравнение. Получим
откуда после преобразований
и, следовательно,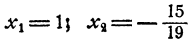 
Соответствующие значения для у равны
Ответ. Система имеет два решения
Тот же прием исключения следует применять при решении систем трех уравнений с тремя неизвестными, если два уравнения имеют первую степень, третье квадратное. При этом из двух уравнений первой степени нужно выразить два неизвестных через третье неизвестное, и полученные выражения подставить в уравнение второй степени.
Таким же образом можно поступать при решении систем я уравнений с п неизвестными при любом я, если все уравнения, кроме одного квадратного, имеют первую степень.
Пример:
Решение:
Перепишем два последних уравнения системы в виде
Решая эту систему относительно х и у по обычным правилам, получим
Подставив эти выражения в первое уравнение, получим
Остается определить соответствующие значения для х и у, что делается подстановкой значений z₁, и z₂ в выражении х и у через z. Мы получим два решения системы:
Системы уравнений, решаемые особыми приемами
В гл. II, § 9 мы рассматривали системы уравнений вида
которые легко решаются при помощи формул Виета. Но, конечно, можно решать такие системы и способом исключения, описанным в предыдущем параграфе.
Часто встречающиеся системы уравнений вида
легко решаются методом исключения, но их можно решать и иначе. Именно, возведя в квадрат второе уравнение и вычитая из него первое, мы получим новое уравнение
которое является следствием данной системы. Объединив его с уравнением
мы получим систему, решаемую при помощи формул Виета.
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то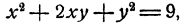 
и следовательно, 2ху = — 8; ху = — 4. Таким образом, из данной системы следует система
для которой получаем два решения
Оба они удовлетворяют уравнениям исходной системы.
Еще проще решаются системы вида
Действительно, х² — y² = (x — у)(х + у), и потому если допустить, что х и у удовлетворяют обоим уравнениям системы, то (х—у) b = а, и следовательно,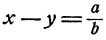 
что вместе с уравнением х + у = b дает систему двух уравнений первой степени с двумя неизвестными, являющуюся следствием исходной системы, которую легко решить. Таким же образом решается и система вида
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то
и следовательно, х + у =b. Решая систему
получим х = 4; v = 1.
Ответ. х = 4; v = 1.
Наконец отметим системы вида
Такие системы уравнений можно решить способом исключения, именно, в силу второго уравнения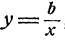 
что при подстановке в первое уравнение дает уравнение относительно х, легко сводящееся к биквадратному.
Однако здесь следует рекомендовать другой прием. Именно, если к первому уравнению добавить, а затем вычесть удвоенное второе, то мы получим новую систему
являющуюся следствием исходной.
Но новая система легко решается, ибо из нее следует, что
и система распадается на 4 системы уравнений первой степени
Следует отметить, что сопоставление результатов решения рассмотренной системы по способу исключения и при помощи указанного искусственного приема приводит к тем же соотношениям, которые были получены из сопоставления двух способов решения биквадратного уравнения.
Системы двух уравнений второй степени, не содержащие линейных членов
Решение системы двух уравнений второй степени с двумя неизвестными общего вида
представляет значительные трудности. Именно, можно доказать, что решение такой системы зачастую сводится к решению уравнения четвертой степени, а нахождение решения общего уравнения четвертой степени представляет довольно сложную задачу, не входящую в рамки курса элементарной алгебры.
Для некоторых систем частного вида возможно элементарное решение. Важным примером таких систем являются системы двух квадратных уравнений, каждое из которых не содержит членов первой степени относительно неизвестных, т. е. системы вида
В этом случае система решается посредством уничтожения свободных членов. Это делается так. Первое уравнение умножается на f₁ второе на f и полученные уравнения вычитаются. Составленное так новое уравнение является следствием исходной системы и имеет вид Ах²+Вху+Су² =0, из которого следует, что
(если только у ≠ 0), откуда мы можем определить отношение
Найдя это отношение, мы можем выразить х через у и затем подставить в одно из уравнений исходной системы. Получившееся в результате неполное квадратное уравнение относительно у легко решается.
Нетрудно видеть, что если А ≠ 0 и хотя бы один из свободных членов в исходных уравнениях отличен от 0, то сделанное выше предположение у ≠ 0 не нарушает общности.
Действительно, если в уравнении Ах² + Вху + Су² == 0 при А ≠ 0 положим у = 0, то и х = 0. Но x = 0; y = 0 не может быть решением исходной системы, если хотя бы один из ее свободных членов отличен от нуля.
Если же коэффициент А = 0, то решение вспомогательного уравнения Вху + Су² = 0 только упрощается, для решения достаточно вынести за скобку у и приравнять к нулю каждый множитель.
Пример:
Решение:
Умножив первое уравнение на 7 и второе на 3, получим после вычитания
Таким образом, х = 22у или х = 2у. Дальнейшее очевидно. Доведя решение до конца, получим четыре решения системы
Решение систем уравнений высших степеней
Задача о решении системы уравнений высших степеней с несколькими неизвестными в общем случае является очень трудной, часто не допускающей решения средствами элементарной алгебры. Однако во многих случаях, комбинируя известные методы решения уравнений и систем уравнений — метод сложения и вычитания, исключения неизвестного с помощью подстановки, введения нового неизвестного— удается найти путь к решению системы. Но в каждой отдельной задаче приходится использовать ее частные особенности для того, чтобы найти удачный метод решения. Рассмотрим несколько примеров.
Пример:
Решить систему уравнений.
Решение:
Способ 1. Из второго уравнения находим, что у = 3 — х. Подставив в первое уравнение, получаем
и, после упрощений,
Соответствующие значения для у будут такими:
Система имеет два решения.
Способ 2. Представим х³ + y³ = 18 как
Принимая во внимание второе уравнение, получим 27 — 9xy = 18, откуда ху = 1. Система
есть следствие исходной, но и исходная есть следствие преобразованной, ибо если х + у = 3; ху = 1, то
Решая преобразованную систему при помощи формул Виета, получим те же два решения:
Пример:
Решение:
Исключение одной из неизвестных величин приводит к решению уравнения четвертой степени, в котором все коэффициенты отличны от нуля. Поэтому лучше избежать этого пути. Это легко сделать, введя новую неизвестную z = xy. Тогда
Таким образом, для z получаем уравнение
откуда z₁ = 47; z₂ = 3.
Итак, данная система расщепилась на две системы:
первая из которых не имеет действительных решений, а вторая имеет следующие решения:
Указанный прием удобно применять к системам двух уравнений с двумя неизвестными, в случае если каждое из уравнений симметрично относительно х и у, т. е. если уравнения не изменяются при перемене х и у местами.
Пример:
Решить систему уравнений:
Решение:
Перемножив уравнения системы, получим
откуда xyz = ±30. Но так как ху = 5, то отсюда следует, что =5z±30 и z = ±6. Теперь х и у легко определить из второго и третьего уравнений системы. Мы приходим к двум решениям:
Пример:
Решить систему уравнений
Решение:
Возвысив обе части первого уравнения в квадрат, получим
Вычитая из этого уравнения второе уравнение данной системы, получим 2x³y³ = 686, откуда (xy)³ = 343; ху = 7. Теперь из первого уравнения данной системы находим, что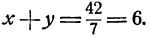 
Итак, решение данной системы свелось к решению системы
Пример:
Решить систему уравнений
Решение:
В первом уравнении раскроем скобки в каждом множителе. Затем поделим обе части обоих уравнений на ху. Получим
Теперь введем новые неизвестные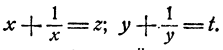 
В новых неизвестных преобразованная система имеет такой вид:
Эта система легко решается. Получаем:
Далее находим значения для х и у из уравнений
Всего получим восемь решений:
Многообразие приемов, которые могут применяться при решении систем уравнений высших степеней, неисчерпаемо, и тем не менее найти путь к решению данной системы удается далеко не всегда. Важно проявлять изобретательность при решении системы в тех случаях, когда это возможно.
Графическое решение уравнений с одним неизвестным
Как уже было сказано, алгебраические методы решения систем уравнений далеко не всегда применимы. Но для целей практики бывает важно находить решения систем уравнений хотя бы приближенно. Эта цель хорошо достигается применением графических методов. Сначала рассмотрим применение графиков к приближенному решению одного уравнения с одним неизвестным.
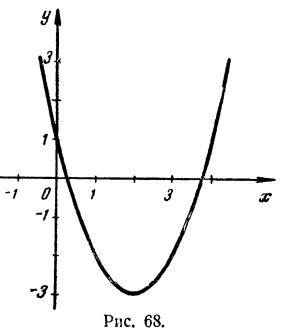
Пусть дано уравнение х²- 4x+1 = 0. Для того чтобы графически решить такое уравнение, рассматриваем неизвестное х как независимое переменное, а левую часть уравнения как функцию этой переменной, т. е. введем в рассмотрение функцию y = x²-4x+1
Решить предложенное уравнение — значит узнать, при каких значениях независимой переменной х функция у обращается в нуль.
Точки графика, соответствующие таким значениям независимой переменной, лежат на оси абсцисс, ибо ордината каждой такой точки равна нулю. Следовательно, интересующие нас точки графика являются точками пересечения графика с осью абсцисс, а корни уравнения x²-4x+1=0 являются абсциссами этих точек пересечения. При этом абсцисса каждой точки пересечения графика с осью абсцисс является корнем уравнения x²-4x+1=0
Строим график функции y = x²-4x+1 Он имеет вид параболы с вершиной в точке (2,-3) (рис. 68). По чертежу находим, что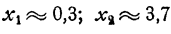 
В действительности
Совершенно такие же рассуждения можно применить к любому уравнению .у —0, где у есть алгебраическое выражение от неизвестной х. Именно, для графического решения такого уравнения нужно построить график выражения у, рассматриваемого как функция от переменной х, и найти точки пересечения этого графика с осью абсцисс. Абсциссы точек пересечения будут корнями уравнения. Конечно, при графическом решении уравнений корни получаются приближенно и довольно грубо, так как на чертеже произвести измерение абсцисс с высокой степенью точности невозможно.
Пример:
Решение:
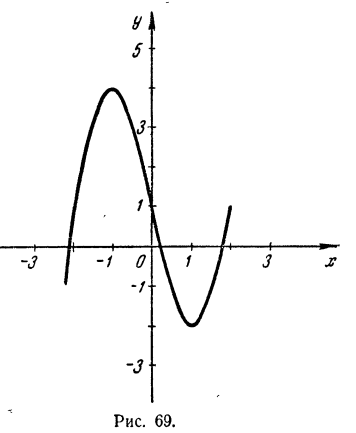
Строим график функции у = x³ — 4x + 1, вычислив предварительно таблицу значений:
По результатам этих вычислений мы видим, что при изменении х от —3 до —2 функция переходит от отрицательных значений к положительным, на участке от 0 до 1 переходит от положительных значений к отрицательным и на участке от 1 до 2 снова от отри-
нательных значений к положительным. На этих участках и следует ожидать, что график пересечет ось абсцисс.
Проводим вычисления для некоторых промежуточных значений х, взятых на этих участках с целью уточнения хода функции:
Теперь построим график по всем вычисленным точкам, соединив их плавной линией (рис. 69).
Из этого чертежа мы получаем:
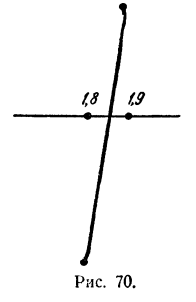
Для того чтобы уточнить значения корней, следует построить в бoльшем масштабе участки графика, примыкающие к корням, вычислив дополнительно значения функции на этих участках. Например, для уточнения корня х₃ проведем следующее вычисление:
Изобразим эти точки на чертеже, приняв большую единицу масштаба (рис. 70).
На таком малом участке изменения х мы вправе считать, что график очень близок к прямой линии. Исходя из этого предположения, получим
Графическое решение систем двух уравнений с двумя неизвестными
Пусть дана система уравнений с двумя неизвестными х и у. Каждое из этих уравнений, взятое отдельно, определяет зависимость между величинами х и у.
Построим на одном чертеже графики этих зависимостей. Числа (x₀y₀), образующие решение системы, должны удовлетворять обоим уравнениям системы, а следовательно, точка с координатами (х₀ у₀) должна лежать на графиках обеих зависимостей, т. е. должна являться точкой пересечения этих графиков.
Обратно, координаты (x₀у₀) любой точки пересечения построенных графиков удовлетворяют обоим уравнениям системы, т. е. образуют решение системы.
Таким образом, для того чтобы графически решить систему двух уравнений с двумя неизвестными, нужно построить график для каждого из уравнений и найти точки пересечения этих графиков. Координаты каждой точки пересечения образуют решение системы.
Пример:
Решить графически систему уравнений
Решение:
Алгебраическое решение этой системы затруднительно. Хотя неизвестное у и легко исключается посредством подстановки в первое уравнение его выражения через дг из второго уравнения, но в результате такого исключения получается уравнение четвертой степени относительно х, решение которого выходит за рамки элементарного курса алгебры.
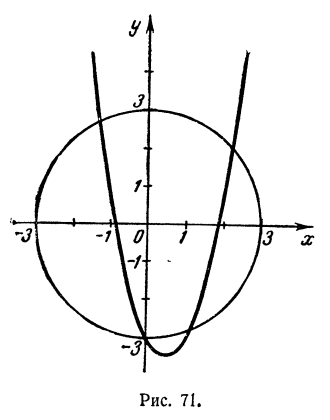
Обратимся к построению графиков. Графиком зависимости х² + у² = 9 является, как мы видели (гл. III, § 3, третий пример), окружность с центром в начале координат и радиусом, равным 3. Графиком зависимости у= 2х² — 2х — 3 является парабола, которую легко построить по таблице значений (рис. 71). Графики пересекаются в четырех точках, координаты которых суть приближенно (—1,2; 2,7); (0; —3); (1,1; —2,8) и (2,2: 2,0).
Следовательно, данная система имеет четыре решения
Второе решение оказывается точным. Остальные три — приближенные.
Графическое решение системы двух уравнений с двумя неизвестными почти не сложнее графического решения одного уравнения с одним неизвестным, а иногда даже проще.
Поэтому часто бывает полезно преобразовать посредством введения нового неизвестного одно уравнение с одним неизвестным в систему двух уравнений с двумя неизвестными, а затем решать эту систему графически. При таком преобразовании следует заботиться о том, чтобы построение графиков обоих уравнений полученной системы было как можно проще.
Рассмотрим несколько примеров на применение этого приема.
Пример:
Решить графически уравнение
Решение:
Представим предложенное уравнение в виде x²=x+1. Мы видим, что в левой и правой частях уравнения находятся некоторые функции от х. Решить уравнение — значит найти, при каких значениях независимого параметра обе функции принимают равные значения. Графически это означает, что нужно найти абсциссы точек пересечения графиков функций у = х² и у =х 1.
Действительно, если при х = а а² = а + 1, то это значит, что точка (а, а²) совпадает с точкой (a, a+1) и, следовательно, принадлежит как графику функции у = х², так и графику функции у = х + 1.
Очевидно и обратное. Если графики функций у = х² и у = x + 1 пересекаются в точке (а, b), то b = a² = a + 1 и, следовательно, при х = а обе функции принимают равные значения. Все сказанное можно коротко изложить так.
Вводим новую неизвестную y = х². Тогда данное уравнение переходит в уравнение у — х—1= 0, которое вместе с введенной зависимостью дает систему
Графиком зависимости у = х² является .парабола, графиком зависимости у = х + 1— прямая линия (рис. 72). Решение задачи дают абсциссы точек пересечения. Они равны приближенно: 
Любое приведенное квадратное уравнение х² + рх + q = 0 может быть решено тем же образом, посредством преобразования в систему
Это удобно тем, что графиком первой зависимости является одна и та же парабола, а графиком второй зависимости является прямая линия, которую очень легко построить в каждом частном случае по двум точкам. Поэтому, тщательно построив в большом масштабе параболу у=х3, мы получаем возможность быстро решать любое приведенное квадратное уравнение.
Подобным образом для решения кубического уравнения, имеющего вид х³ + рх + q = 0, достаточно заготовить график функции у = х³. Абсциссы точек пересечения этого графика с прямой у + рх + q = 0 дают корни уравнения x³ + + q = 0.
Пример:
Превратив в систему, решить графически уравнение
Решение:
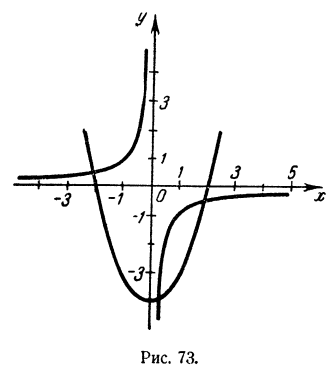
Это делают приемом, указанным выше. Однако это можно сделать и иначе. Именно, перепишем уравнение в виде х(х² — 4)+1=0
и положим х² — 4 = у. Уравнение заменится системой
Графиком первого уравнения системы является парабола, графиком второго — гипербола (рис. 73). Абсциссы точек пересечения суть 
Этим приемом можно решить любое кубическое уравнение
Графиком первого уравнения является парабола, графиком второго — гипербола.
Решение уравнения четвертой степени ах⁴ + bх² + сх + d = 0 при с ≠ 0 легко сводится к определению точки пересечения двух парабол.
Для этого вводим новое неизвестное у = х² У и уравнение заменяем системой
Графиком первого уравнения является парабола с вершиной в начале координат и осью, совпадающей с осью ординат. Графиком второго уравнения тоже является парабола, но только ее ось параллельна оси абсцисс. Действительно, решив второе уравнение относительно х, мы получим
т. с. х является квадратичной функцией от у, графиком которой является парабола с осью, параллельной оси абсцисс.
Из рассмотренных примеров ясно, что каждое данное уравнение с одним неизвестным можно преобразовать а систему двух уравнений с двумя неизвестными многими способами и при выборе какого-нибудь способа следует заботиться о наиболее выгодном расположении графиков на чертеже.
Уточнение корня уравнения или решения системы нелинейных уравнений, исходя из грубого приближения
При графическом решении корень уравнения или решение системы уравнение определяется лишь грубо приближенно. Уточнение результата за счет увеличения масштаба не очень эффективно, так как повышение точности требует пропорционального увеличения масштаба. Например, чтобы определить новую значащую цифру после занятой в десятичном разложении корня, т. е. увеличить точность в 10 раз, нужно и масштаб увеличить в 10 раз.
Однако существует весьма хорошо действующий алгебраический способ для подобного рода уточнения. Мы не будем излагать его в общем виде, а ограничимся только рассмотрением примеров его применения.
Пример:
Для уравнения x³ — 4x + 1= 0 известно приближенное значение одного из корней х ≈1,8. Требуется вычислить этот корень с большей точностью.
Решение:
Поступаем так. Положим x =1,8 + h, где h — новая неизвестная. Мы можем быть уверены, что h есть маленькое число, во всяком случае меньшее, чем 0,1. Подставив в уравнение вместо х его выражение через h, получим
Так как h² меньше h во столько же раз, во сколько h меньше единицы, для приближенного вычисления h отбросим в полученном уравнении члены с h² и h³. Получим
Для дальнейшего уточнения мы можем еще раз применить тот лее прием. Положим x≈1,86 + h₁,. Для h₁ получим, отбрасывая члены, содержащие h₁² и h₁³, приближенное уравнение
(При этом нет надобности вычислять коэффициенты при h₁² и h₁³ , ибо соответствующие члены мы все равно отбрасываем.) Отсюда h≈ 0,0008 и, следовательно,x ≈ 1,8608.
Продолжая этот прием, мы можем получить значение корня уравнения с любой степенью точности.
В общем виде идея метода такова. Если х₀ есть приближенное значение корня данного уравнения, мы полагаем в уравнении x= x₀ + h и в полученном уравнении относительно h отбрасываем члены, содержащие h выше, чем в первой степени, и решаем приближенно получившееся уравнение первой степени относительно h. Тогда число x₁ = x₀ + h оказывается, вообще говоря, значительно лучшим приближением к корню, чем исходное приближение х₀. В случае надобности процесс можно повторить.
Пример:
Для одного решения системы уравнений
известны приближенные значения х ≈ 2,2, у ≈ 2,0. Найти решение с большей точностью.
Решение:
Будем действовать тем же способом, как при уточнении корня одного уравнения с одним неизвестным. Именно, положим x = 2,2 + h; .у = 2,0 + к и, подставив в уравнение, отбросим все члены, содержащие h², k², hk, так как эти величины значительно меньше самих h и k. Получим
Решив эту систему, получим h ≈ — 0,03, k ≈ 0,07. Таким образом, уточненными значениями для х и у являются значения
Для дальнейшего уточнения можно повторить тот же процесс.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: \( -2<,>34 \)
Ввод: -1,15
Результат: \( -1<,>15 \)
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -\frac<2> <3>$$
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5\frac<8> <3>$$
Помните, что на ноль делить нельзя!
RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система \(m\) линейных алгебраических уравнений с \(n\) неизвестными (сокращенно СЛАУ) представляет собой систему вида
\( \left\< \begin
Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от \(n\) переменных \( x_1 , \ldots x_n \), а линейными потому, что эти многочлены имеют первую степень.
Числа \(a_
СЛАУ называют однородной, если \( b_1 = b_2 = \ldots = b_m = 0 \). Иначе её называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных \( x_1^\circ, \ldots , x_n^\circ \), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При \(m=n\), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Рассматривая коэффициенты \(a_
\( \begin
или, обозначая столбцы соответственно \( a_1 , \ldots , a_n , b \),
\( x_1 a_1 + x_2 a_2 + \ldots + x_n a_n = b \tag <2>\)
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца \(b\) в виде линейной комбинации столбцов \( a_1, \ldots, a_n \). Соотношение (2) называют векторной записью СЛАУ.
Поскольку \(A \;,\; X\) и \(B\) являются матрицами, то запись СЛАУ (1) в виде \(AX=B\) называют матричной. Если \(B=0\), то СЛАУ является однородной и в матричной записи имеет вид \(AX=0\).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида \(AX=B\)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
\( A = \begin
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
\( (A|B) = \left( \begin
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ \(AX=B\) необходимо и достаточно, чтобы ранг её матрицы \(A\) был равен рангу её расширенной матрицы \( (A|B) \).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = \frac<\Delta_i> <|A|>\;,\quad i=\overline <1,n>\tag <3>$$
где \(\Delta_i\) — определитель матрицы, получающейся из матрицы \(A\) заменой \(i\)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
Однородные системы
Теорема. Если столбцы \( X^<(1)>, X^<(2)>, \ldots , X^ <(s)>\) — решения однородной СЛАУ \(AX=0\), то любая их линейная комбинация также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Естественно попытаться найти такие решения \( X^<(1)>, \ldots , X^ <(s)>\) системы \(AX=0\), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение. Любой набор из \(k=n-r\) линейно независимых столбцов, являющихся решениями однородной СЛАУ \(AX=0\), где \(n\) — количество неизвестных в системе, а \(r\) — ранг её матрицы \(A\), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице \(A\) однородной СЛАУ \(AX=0\) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Теорема. Пусть дана однородная СЛАУ \(AX=0\) с \(n\) неизвестными и \( \text
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ <(1)>+ \ldots + c_kX^ <(k)>$$
где постоянные \( c_i \;, \quad i=\overline <1,k>\), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ \(AX=B\). Заменив столбец \(B\) свободных членов нулевым, получим однородную СЛАУ \(AX=0\), соответствующую неоднородной СЛАУ \(AX=B\). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец \(X^\circ\) — некоторое решение СЛАУ \(AX=B\). Произвольный столбец \(X\) является решением этой СЛАУ тогда и только тогда, когда он имеет представление \(X = X^\circ + Y \), где \(Y\) — решение соответствующей однородной СЛАУ \(AY=0\).
Следствие. Пусть \(X’\) и \(X»\) — решения неоднородной системы \(AX=B\). Тогда их разность \( Y = X’ — X» \) является решением соответствующей однородной системы \(AY=0\).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение \(X^\circ\) этой системы, чтобы свести её к однородной системе.
Теорема о структуре общего решения СЛАУ. Пусть \(X^\circ\) — частное решение СЛАУ \(AX=B\) и известна фундаментальная система решений \( X^<(1)>, \ldots , X^ <(k)>\) соответствующей однородной системы \(AX=0\). Тогда любое решение СЛАУ \(AX=B\) можно представить в виде $$ X = X^\circ + c_1 X^ <(1)>+ c_2 X^ <(2)>+ \ldots + c_k X^ <(k)>$$
где \( c_i \in \mathbb
Эту формулу называют общим решением СЛАУ.
Основные методы решения систем повышенной сложности
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим изучение всех трех основных методов решения систем уравнений и их комбинаций на примере решения систем повышенной сложности. А также рассмотрим некоторые специфические приемы для упрощения различных типов систем.
http://www.math-solution.ru/math-task/slau
http://interneturok.ru/lesson/algebra/9-klass/sistemy-uravneniy/osnovnye-metody-resheniya-sistem-povyshennoy-slozhnosti