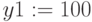
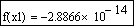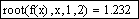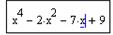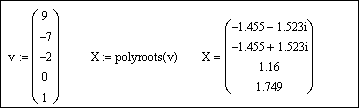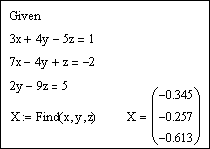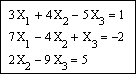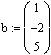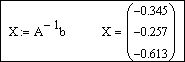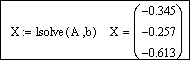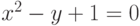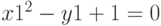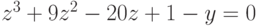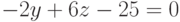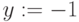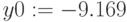Решение систем уравнений с помощью блока given

Решение систем уравнений с помощью блока given

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

• отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
• уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

• f(x) – функция левой части уравнения f(x) = 0;
• x – переменная, относительно которой требуется решить уравнение;
• a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

1. задается матрица коэффициентов при неизвестных системы A;
2. задается столбец свободных членов b;
3. вводится формула для нахождения решения системы X:=A -1 b;
4. выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

1. Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
2. Сохранить в личной папке на диске z:\ новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3. Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

1. В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
2. Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

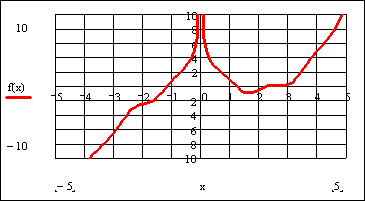
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

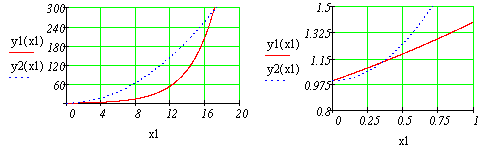
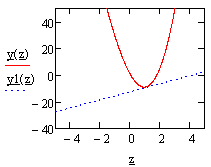
После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .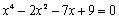

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 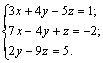Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

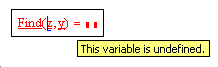
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Основные сведения. Простые вычисления

Решение систем уравнений с помощью блока Given-Find

Решение систем уравнений MathCAD осуществляет численными методами. При этом должно быть задано некоторое начальное приближение для тех переменных, значение которых необходимо найти. Основываясь на этих начальных данных, MathCAD будет последовательно уточнять решение до тех пор, пока не подберет наиболее точные значения. Проблемы возникают, когда нелинейная система имеет несколько решений. За один раз MathCAD находит только одно решение, которое обычно более близко к заданному начальному приближению. Поэтому в таких случаях необходимо решать систему несколько раз с различными начальными приближениями.

Решающий блок состоит из нескольких компонент, следующих на листе в строго определенном порядке :

1. Начальное приближение (присваивание начальных значений переменным).

2. Директива Given , которую необходимо набрать с клавиатуры.

3. Уравнения, которые необходимо решить. Уравнения вводятся в обычной математической форме, но вместо простого знака равенства «=» используется оператор логического равенства (вводится путем нажатия Ctrl-= ).

4. Обращение к функции Find . Аргументами функции являются имена переменных, относительно которых решается система. Функция возвращает вектор значений, где первый элемент соответствует первой переменной в списке аргументов, второй элемент — второй переменной и так далее.

Пример . Решим систему нелинейных уравнений:

Данная система имеет два решения. Найдем одно из них (рис. 5) с начальным приближением x = 0; y = 0.

Рис. 5. Решение системы в MathCAD

Последняя запись — вектор (-1; -2) есть значение, которое вернула функция Find, то есть одно из решений системы. Найти второе решение можно, если взять другое начальное приближение x = 2; y = 2. Тогда функция Find вернет вектор (2; 4).

Начиная с MathCAD 2000 существует возможность одновременно найти несколько решений . Для этого система уравнений и начальные приближения должны быть переписаны в векторной форме (рис. 6). Каждая переменная будет вектором, содержащим столько компонент, сколько решений находится. В системе изменения коснутся преимущественно членов с перемножением переменных. Допустим, что в уравнении присутствует выражение x*x. Если x = (x 1 ; x 2 ) — вектор, то . Нам же необходим результат поэлементного перемножения . Для этого существует специальная операция, записываемая как .

Рис. 6. Пример одновременного поиска нескольких решений

Изменения коснулись и части получения результата. В данном случае функция Find вернет вектор из двух элементов, которые мы обозначили как X и Y. Каждый из этих элементов есть вектор значений x или y для решений. Соответственно первое решение — (-1; -2); второе решение — (2; 4).

Аналитическое решение линейных и нелинейных систем уравнений

Данное решение используется для получения решений в общем виде. Обычно при этом система уравнений записывается только с использованием буквенных обозначений переменных, без конкретных чисел. Для получения аналитического решения (рис. 7, 8) используется оператор аналитического вычисления «» вместо оператора числового вычисления «=».

Рис. 7. Пример аналитического решения нелинейной системы

Рис. 8. Пример аналитического решения линейной системы

Следует обратить внимание, что здесь при решении системы нелинейных уравнений в блоке Given-Find уже нет необходимости указывать начальные приближения, поскольку решение идет не численными, а символьными методами (используется ядро математической системы Maple).

Работа с последовательностями. Законы вычисления элементов матриц

MathCAD позволяет задавать значения элементов матриц не только по отдельности, но и путем определения общих законов вычисления элементов. При этом возникает необходимость определить границы действия законов, то есть диапазоны изменения индексов матриц. Для этого широко используются последовательности.

Замечание : в MathCAD нумерация элементов векторов и матриц начинается с нуля.

Пример . Ряд чисел Фибоначчи определяется по следующим правилам:

F i = F i-1 + F i-2 ; i>2.

Данный ряд бесконечен. Но мы не можем определить в MathCAD бесконечные последовательности, возможно лишь нахождение части ряда. Поэтому вместо указания i>2 необходимо задать конкретный диапазон изменения индекса i, например нас могут интересовать члены ряда со третьего по восьмой. Решение показано на рис. 9.

Рис. 9. Вычисление части ряда чисел Фибоначчи в MathCAD

Здесь сначала определен диапазон изменения индекса i, затем заданы значения двух первых членов ряда и записана общая формула для вычисления члена с индексом i. Последняя часть (столбец значений) есть часть ряда F 3 .. F 8 , вычисленная системой. Такой порядок записи выражений объясняется тем, что MathCAD вычисляет формулы последовательно, в порядке «слева направо и сверху вниз». При вычислении члена F 3 по заданной рекуррентной формуле системе уже должны быть известны реальные значения F 1 и F 2 . Поэтому они должны быть записаны до этой формулы.

Пример . Рассмотрим численное интегрирование явным методом Эйлера.

Сначала кратко рассмотрим суть метода. Пусть дано дифференциальное уравнение в общем виде:

; x(t 0 ) = x 0 ;

.

Необходимо проинтегрировать данное уравнение. Если функция F(x,t) достаточно сложна, то такое уравнение может не иметь очевидного аналитического решения. В таких случаях необходимо использовать приближенные численные методы, к которым и относится метод Эйлера.

Прежде всего необходимо заменить производную каким-либо приближенным соотношением. Воспользуемся определением производной:

.

К сожалению, компьютеры не могут непосредственно работать с бесконечно малыми величинами. Поэтому перейдем к конечным величинам:

.

Такая простая формула будет тем точнее, чем меньше . В любом случае в решение вносится погрешность, которая будет оказывать более или менее существенное влияние на соответствие результата точному решению. Рассмотрение этого вопроса выходит за рамки данного пособия. В первом приближении можно рекомендовать выбирать в диапазоне .

Далее вводится дискретное время:

где — шаг интегрирования по времени; — номер конечного шага интегрирования. Функцию F(x,t) можно вычислять как в точке (x i ,t i ), так и в точке (x i+1 ,t i+1 ) — это не влияет на точность метода, хотя может влиять на характер роста погрешности. Первый вариант соответствует явному методу Эйлера, второй — неявному.

,

из которого следует расчетная формула явного метода Эйлера

.

Рассчитаем переходный процесс в электрической цепи:

Учитывая, что здесь сумма напряжений на резисторе и конденсаторе равна нулю, а ток, протекающий через резистор, равен току через конденсатор, то есть , можно вывести дифференциальное уравнение

.

Пусть R = 1, C = 1 с начальным условием U c (0) = 1. Введем дискретное время:

;

где h — шаг интегрирования по времени; N — номер конечного шага интегрирования. Воспользуемся расчетной формулой явного метода Эйлера

;;

.

Предположим, что нас интересуют пять итераций с шагом по времени 0,1. Решение можно записать в двух формах (рис. 10).

Рис. 10. Две формы записи решения в MathCAD

Форма (а) более проста, но не позволяет записывать решения систем дифференциальных уравнений, правые части которых являются взаимозависимыми . Вторая форма (б) более универсальна.

Полученный вектор U c содержит значения U c (t i ) для заданных дискретных моментов времени. Можно легко убедиться, что полученное численное решение похоже на точное аналитическое . Добавим следующие выражения:

и сравним полученные значения R (точное решение) и U c . В MathCAD существуют специальные стандартные средства интегрирования дифференциальных уравнений (функция rkfixed, блок Given-Odesolve), которые будут рассмотрены далее.

Функции и графики функций

MathCAD допускает определение на листе новых функций от одного и более аргументов. Определение записывается в строчку в следующем порядке:

1. Имя новой функции. На имена функций распространяются те же правила, что и на имена переменных.

2. Список аргументов в круглых скобках через запятую.

3. Стандартный символ присваивания «:=».

4. Выражение, определяющее значение функции от аргументов.

Обращение к функции записывается в традиционной математической форме: упоминание имени функции, сразу после которого идет список значений аргументов в круглых скобках через запятую.

Возможно построение следующих типов графиков:

1. Линейный (в прямоугольных и полярных координатах).

2. Линии уровня поверхности.

4. Столбиковая диаграмма.

5. Точечный и векторный графики поверхности.

Для построения любого графика необходимо сначала определить на листе все данные, необходимые для построения, затем вставить на лист соответствующий графический регион и связать его с отображаемыми данными. Для вставки графического региона можно использовать соответствующие кнопки панели Graph либо выбрать требуемый пункт в верхнем меню Insert\Graph (или Вставка\График ). Связь с отображаемыми данными производится путем указания этих данных в позициях ввода графического региона.

Для регионов линейных графиков (рис. 11) заполняются две основные позиции ввода — слева и снизу от графика.

Рис. 11. Вид региона для линейного графика до (а) и после (б) заполнения одной из основных позиций ввода

В нижней позиции 2 указывается выражение, определяющее значения абсцисс графика. Выражение — имя последовательности, вектора или обычной переменной. Может быть несколько выражений через запятую. При необходимости можно указать в дополнительных позициях 3 и 4 минимальное и максимальное значения.

В позиции 1 указывается выражение, определяющее значения ординат графика. Можно перечислить несколько выражений через запятую — в этом случае будет построено несколько графиков в одних координатах . Выражения обычно являются функциями от аргумента, указанного в позиции 2. Тем не менее, могут быть построены и графики от двух функций заданных параметрически, в этом случае в позициях 1 и 2 указываются имена этих функций (рис. 12).

Рис. 12. Фрагмент листа MathCAD с линейными графиками двух функций (параметрической (x(t); y(t)) и обычной f(t))

Для регионов графиков поверхностей заполняется одна позиция ввода. Для графиков вида z = f(x,y) указывается либо имя соответствующей функции от двух переменных, либо имя матрицы, содержащей значения z.

Для параметрических графиков (заданных функциями вида x = f 1 (u,v); y = f 2 (u,v); z = f 3 (u,v)) есть два способа построения. Рассмотрим наиболее универсальный способ. Построим график конусовидной поверхности, заданной параметрически:

Пусть параметр u изменяется от 0 до с шагом , а параметр v — от 0 до 15 с шагом 1. Необходимо определить законы вычисления трех матриц, каждая из которых будет содержать значения одной из координат точек поверхности. Число измерений каждой матрицы обычно равно числу параметров поверхности (в данном случае матрицы двумерные). Индексы последних элементов матрицы по каждому измерению определяются по формуле , где p max , p min — максимальное и минимальное значения параметров соответственно; p s — шаг параметра. Индексы первых элементов матриц равны нулю.

На листе MathCAD (рис. 13) сначала определяются последовательности, определяющие диапазоны изменения индексов матриц. Затем записываются законы вычисления векторов, содержащих значения параметров. Данные законы имеют общий вид , где p — вектор параметров; k — индекс. Далее записываются законы вычисления матриц с координатами. Такими законами являются исходные параметрические выражения для координат, в которых вместо имен параметров подставляются элементы соответствующих векторов параметров. В последнюю очередь добавляется регион графика поверхности, где в позиции ввода в круглых скобках через запятую перечисляются имена трех матриц, содержащих значения координат x,y,z, причем размерности матриц должны совпадать.

Второй способ построения параметрических поверхностей: на листе непосредственно записываются три параметрические функции, определяющие координаты, добавляется регион графика поверхности, после чего в позиции ввода региона в круглых скобках через запятую перечисляются имена указанных функций (без параметров).

Рис. 13. Построение конусовидной поверхности в MathCAD

Недостаток второго способа: MathCAD выберет диапазоны изменения параметров самостоятельно. Такой способ вполне пригоден для построения различных поверхностей вращения, все параметры которых находятся под функциями синуса или косинуса (например, тор или сфера).

Изменить различные параметры отображения графиков можно в специальном окне настроек, которое вызывается из раздела верхнего меню ( Format\Graph или Форматирование\График ).

Решение задач нецелочисленной оптимизации

Задача нецелочисленной оптимизации состоит в том, чтобы подобрать такие значения аргументов целевой функции, при которых данная функция принимает экстремальное (минимальное или максимальное) значение и соблюдается заданная система ограничений на значения аргументов. В математической форме задача может быть сформулирована следующим образом:

где f — целевая функция; n — количество аргументов целевой функции; g i , h i — элементы системы ограничений (равенств или неравенств различного вида); k — количество ограничений.

Пример задачи оптимизации. Предположим, что некоему студенту необходимо сдать два зачета в один день. Он поставил себе задачу сдать их как можно лучше, причем так, чтобы оценка за каждый зачет была не меньше 2,5 баллов. У него осталось 24 часа. Студент предположил, что, потратив один час на первый предмет, он повысит возможную оценку на 0,5 балла, потратив тот же час на второй предмет, — повысит оценку по нему на 0,25 балла. Необходимо определить, сколько часов (x) ему надо потратить на первый предмет и сколько (y) на второй предмет, чтобы выполнить поставленную задачу. Математически задача запишется так:

(сумма оценок по предметам),

и должны выполняться следующие ограничения:

В системе MathCAD такие задачи решаются с помощью блоков Given-Maximize и Given-Minimize. Так же, как и при решении систем уравнений, решающий блок состоит из нескольких компонент, следующих на листе (рис. 14) в строго определенном порядке :

1. Присваивание начальных значений переменным, относительно которых решается задача оптимизации.

2. Определение целевой функции.

3. Директива Given .

4. Ограничения, записываемые в обычной математической форме. Могут использоваться все указанные выше знаки отношений, но вместо простого знака равенства «=» используется оператор логического равенства (вводится путем нажатия Ctrl -=). Замечание : система MathCAD при минимизации и максимизации воспринимает знаки строгого неравенства ( ) как знаки нестрогого неравенства .

5. Обращение к одной из функций Minimize или Maximize для соответственно минимизации или максимизации. Первым аргументом всегда является имя целевой функции. Далее следуют имена переменных, относительно которых решается задача. Функция возвращает вектор значений, где первый элемент соответствует первой переменной в списке аргументов, второй элемент — второй переменной и так далее.

Рис. 14. Решение задачи о студенте в системе MathCAD

Здесь система MathCAD определила, что решением задачи являются значения: x = 10 часов, y = 14 часов.

Численное решение дифференциальных уравнений

Рассмотрим стандартные средства численного решения дифференциальных уравнений и систем дифференциальных уравнений.

Численное решение одного дифференциального уравнения

MathCAD 2000 позволяет без дополнительных преобразований численно решить дифференциальное уравнение, явно разрешенное относительно старшей производной (рис. 15).

Рис. 15. Примеры уравнений, разрешенного (а) и неразрешенного (б) относительно старшей производной

Решение осуществляется с помощью специального блока Given-Odesolve , состоящего из следующих компонент:

1. Директива Given .

2. Дифференциальное уравнение, записанное в традиционной математической форме со следующими особенностями: а) вместо простого знака равенства «=» используется оператор логического равенства (вводится нажатием Ctrl-= ); б) при обозначении интегрируемой функции всегда указывается аргумент (то есть вместо функции x(t) нельзя писать просто x); в) при записи производных используются либо стандартные операторы и , либо ставятся (с помощью Ctrl-F7 ) символы производной, например x’(t), x’’(t).

3. Указание начальных или конечных значений интегрируемой функции и ее производных (за исключением старшей), входящих в уравнение . Значения вводятся в традиционной форме с использованием оператора логического равенства. Число значений должно совпадать с порядком уравнения. Для уравнения второго порядка вида должны быть заданы начальные значения функции и ее первой производной, например x(0) = 1; x’(0) = 0,5. Для ввода символа производной «’» используется комбинация клавиш Ctrl-F7 .

4. Обращение к функции Odesolve . Первый аргумент — всегда имя независимой переменной. Второй аргумент — конечное значение независимой переменной. Третий (необязательный) аргумент — количество промежуточных точек решения. Odesolve возвращает функцию, представляющую приближенное (численное) решение дифференциального уравнения на заданном интервале времени. Данная функция может быть использована для определения значений интегрируемой функции в различных точках, а также для построения графика.

Пример . Решим вышеуказанное дифференциальное уравнение при значениях t = 0..5; найдем значения x при t = 2; 4, и построим график решения.

Численное решение систем дифференциальных уравнений с использованием Odesolve возможно только начиная с версии MathCAD 11. В более старых версиях можно воспользоваться специальными функциями (rkadapt, rkfixed, bulstoer).

Численное решение систем обыкновенных дифференциальных уравнений

Дифференциальные уравнения, входящие в систему, должны иметь первый порядок (то есть содержать только первые производные). Все уравнения должны быть предварительно разрешены относительно производных и записаны в нормальной форме вида

.

Для преобразования уравнений в нормальную форму есть два основных подхода:

1. Понижение порядка уравнений путем замены переменных . Если исходное дифференциальное уравнение порядка q (q>1) имеет вид

,

то вводятся новые переменные p j , причем j = 1..q-1. В исходном уравнении производится серия замен:

,

а производная высшего порядка заменяется производной первого порядка:

.

Добавляется q – 2 новых уравнений вида

.

Добавляется еще одно уравнение

.

можно преобразовать в систему уравнений:

2. Приведение системы дифференциальных уравнений к явному виду путем ее решения относительно производных. Например, решая систему

относительно и , получим:

Рассмотрим решение систем дифференциальных уравнений в MathCAD на примере задачи о моделировании динамики электрической цепи, показанной на рис. 16.

Динамика описывается следующей системой дифференциальных уравнений:

Рис. 16. Электрическая цепь

где U c — напряжение на конденсаторе. Пусть ; i 1 (0) = i 2 (0) = U c (0) = 0; ; L 1 = 0,02; L 2 = 0,06; M = 0,01; R = 0,5; C = 0,01.

Решение записывается следующим образом:

1. Определяются все константы и вспомогательные функции, присутствующие в правой части системы.

2. Определяется специальная функция, вычисляющая правую часть системы. Функция имеет два аргумента: первый — независимая переменная (например, время t), второй — вектор текущих значений зависимых переменных. Результатом функции должен быть вектор, содержащий значения правых частей системы, вычисленных по значениям второго аргумента функции. Векторы имеют столько элементов, сколько уравнений в системе. При записи правых частей все зависимые переменные заменяются элементами вектора – второго аргумента, причем используется следующее правило : нулевому элементу соответствует переменная, производная от которой стоит в левой части первого уравнения; первому элементу — переменная, производная от которой стоит в левой части второго уравнения и так далее. В приведенном далее примере, где второй аргумент функции обозначен как Y, элементу Y 0 соответствует i 1 — переменная из производной в левой части первого уравнения, элементу Y 1 соответствует i 2 — переменная из производной в левой части второго уравнения, элементу Y 2 соответствует U C .

3. Задается вектор начальных значений независимых переменных.

4. Обращение к функции rkfixed . Первый аргумент — вектор начальных значений. Второй и третий — соответственно начальное и конечное значения независимой переменной. Четвертый аргумент — число промежуточных точек решения (обычно достаточно большое число в диапазоне ). Пятый — имя функции, вычисляющей правую часть системы. Функция rkfixed возвращает матрицу, в нулевом столбце которой находятся значения независимой переменной, а в прочих столбцах — соответствующие значения зависимых переменных.

Решение показано на рис. 17.

Рис. 17. Запись решения задачи в MathCAD

На рис. 18 показаны графики i 2 (t), U c (t). Данным переменным соответствуют второй и третий столбцы матрицы S.

Рис. 18. Графики i 2 (t), U c (t)

Некоторые стандартные функции MathCAD

Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:

M — квадратная матрица;

V — вектор (матрица из одного столбца);

A — произвольная матрица;

S — симметричная матрица;

G — произвольная матрица или число;

X — вектор или число;

Z — комплексная матрица или число;

z — комплексное число;

прочие символы — скалярные величины.

Экспоненциальные и логарифмические функции

exp(X) — экспонента от X;

ln(X) — натуральный логарифм от X;

log(X) — десятичный логарифм от X;

log(X,b) — логарифм от X по основанию b.

Гиперболические и тригонометрические

(прямые и обратные) функции

sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) — соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах ;

sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) — аналогичные гиперболические функции;

asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) — соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.

Функции для работы с комплексными числами

Re(Z), Im(Z) — соответственно вещественная и мнимая части комплексного числа Z;

arg(z) — аргумент комплексного числа z (в радианах).

length(V) — возвращает число элементов вектора V;

cols(A) — возвращает число столбцов матрицы A;

rows(A) — возвращает число строк матрицы A;

matrix(m,n,f) — матрица размером mxn, значения элементов матрицы определяются f — функцией f(i,j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;

identity(n) — единичная матрица ;

tr(M) — след матрицы M (сумма элементов главной диагонали);

rank(A) — ранг матрицы M;

norme(M) — эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;

eigenvals(M) — вектор, элементы которого являются собственными числами матрицы M;

eigenvecs(M) — матрица, состоящая из нормализованных собственных векторов матрицы M;

cholesky(S) — возвращает нижнетреугольную матрицу L — результат разложения Холецкого вида ;

lu(M) — возвращает матрицу размера , состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида .

Пример вычислений с матричными функциями : нахождение собственного числа путем решения матричного уравнения и с помощью функции eigenvals.

Элементы статистического анализа данных

gmean(G1,G2,G3…) — среднее геометрическое аргументов;

mean(G1,G2,G3…) — среднее арифметическое аргументов;

stdev(G1,G2,G3…) — среднеквадратичное отклонение.

fft(V1), ifft(V2) — прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 — вектор из 2 m элементов, V2 — вектор из 1 + 2 m-1 элементов, m>2;

cfft(A), icfft(A) — прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;

wave(V), iwave(V) — прямое и обратное вейвлет-преобразования, V — вектор из 2 m элементов, m — целое число.

Аппроксимация, интерполяция и экстраполяция

Аппроксимация — поиск функции, которая с заданной степенью точности описывает исходные данные.

Интерполяция — определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).

Экстраполяция — определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).

Применяются следующие функции MathCAD:

regress(VX,VY,k) — возвращает вектор данных, используемый для поиска интерполирующего полинома порядка k. Полином должен описывать данные, состоящие из упорядоченных значений аргумента (VX) и соответствующих значений неизвестной функции (VY), то есть график полинома должен проходить через все точки, заданные координатами (VX,VY), или максимально близко к этим точкам;

interp(VS,VX,VY,x) — возвращает интерполированное значение неизвестной функции при значении аргумента x. VS — вектор значений, который вернула функция regress. VX,VY — те же данные, что и для regress. Функции interp и regress используются в паре;

predict(V,m,n) — возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.

Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов .

Примеры интерполяции и экстраполяции:

1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.

2. Дана функция y(i) = e –i/10 *sin(i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.

Решения показаны на рис. 19.

Рис. 19. Решения в MathCAD первой (а) и второй (б) задач

Нахождение корней полинома

polyroots(V) — возвращает вектор, содержащий все корни полинома , заданного вектором-столбцом коэффициентов

.

max(G1,G2,…) — максимальное значение среди аргументов;

min(G1,G2,…) — минимальное значение среди аргументов;

if(a,b,c) — возвращает b, если , иначе возвращает c;

sign(a) — возвращает –1, 0 или 1 в зависимости от знака числа a.

На рис. 20 показан пример применения функции if.

Рис. 20. Функция, вычисляющая факториал

Элементы программирования в MathCAD

На одном листе MathCAD могут определяться один или несколько программных блоков. Обычно их используют при разработке функций, которые осуществляют какую-либо сложную обработку данных, например находят корень нестандартного уравнения.

Переменные . В программном блоке можно читать значения переменных, определенных в MathCAD до этого блока. Однако изменить значения этих переменных внутри программного блока невозможно . Все переменные, которым присваиваются значения внутри программного блока, будут локальными переменными, которые недоступны вне блока. Специально объявлять переменные не нужно, достаточно просто присвоить им значения. Если программный блок является телом функции, то он также может читать значения аргументов этой функции.

Программный блок представляет собой группу операторов присваивания и управляющих операторов. Необходимо обратить особое внимание, что все ключевые слова (например, if ) в этих операторах обязательно вводятся с помощью панели Programming ( Программирование ). Их ввод с клавиатуры — ошибка!

В целом правила работы с операторами те же, что и в языке Pascal, отличия касаются способа записи операторов.

Таблица 2. Соответствие программных операторов MathCAD и Pascal

Что такое given в mathcad

Решение уравнений

При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given — и имеющий следующую структуру:

Выражения с функцией Find()

Find(vl, v2, …, vn) — возвращает значение одной или ряда переменных для точного решения;

Знак равенства в уравнениях вызывается с математической панели БУЛЕВО(Boolean) или с клавиатуры клавишами «CTRL http://www.intuit.ru/2010/edi» >

Как и в предыдущем случае, сначала необходимо провести локализацию корней – задание начальной точки, от которой будет происходить поиск решения. Решение ищется методом итераций и при наличии нескольких корней, очевидно, будет найдено лишь ближайшее решение, если оно существует. Блок Given…Find(.) можно использовать и для решения уравнений одним неизвестным.

Пример 4.4

Решить систему уравнений 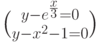>=0\choose y-x^2-1=0>»>.

Осуществляется решение системы нелинейных уравнений при помощи блока Given…Find(.) (Рис.4.3).

• Локализация корней: задаем систему уравнений, строим график.
• По графику определяем три корня.
• Задаем последовательно разные начальные значения корней.

>»>

,

>-y=0″>

0.354 \\ 1.125 \end

,

>-y=0″>

-2.631 \cdot 10^ \\ 1 \end

,

>-y1=0″>

17.015 \\ 290.506 \end

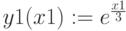
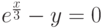
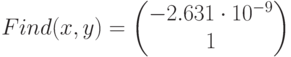
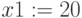
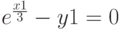
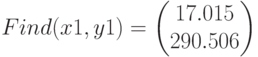
Поиск корней при помощи блока Given Minerr()

Функция Minerr использует тот же самый алгоритм, что и функция Find. Различие состоит в следующем. Функция Find ищет решение с заданной точностью и, если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, то она возвращает сообщение об ошибке. Функция Minerr возвращает это приближение. Системная переменная ERR дает величину ошибки.

Minerr (vl, v2, …, vn ) возвращает значения ряда переменных для приближенного решения.

Minerr() пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения. При использовании функции Minerr обязательно предусматривать проверку решений. Полезно как можно точнее указывать начальные приближения к решению.

Пример 4.5

Решить систему уравнений «>.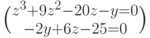

Решаем при помощи блока Given…Find(.) (Рис.4.4).

• Локализация корней: задаем систему уравнений, строим график.
• Графики имеют точку касания. Функция . Find( ) не решает систему.
• Функция Minerr() дает приближенное решение. Системная переменная ERR=0.37. Это ошибка определения корня. Проверка показывает максимальную ошибку 0.33.

,

Система не решается:

,

1.082 \\ -9.169 \end

,

Решение уравнений с помощью функции Find(x)

Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:

— задать начальное приближение

— ввести служебное слово

• — записать уравнение, используя знак боулево равно
• — написать функцию find с неизвестной переменной в качестве параметра

В результате после знака равно выведется найденный корень.

Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.

В Mathcad можно писать программы двух видов

• 1)в виде скриптов(последовательность команд)
• 2)в виде настоящих программ с входными и выходными параметрами.

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).

Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).

Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Вычислительный блок Given/Odesolve

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:

• Given — ключевое слово;
• ОДУ и начальное условие, записанное с помощью логических операторов, причем начальное условие должно быть в форме у (t1) = b;
• odesoive(t, t1) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).

Допустимо, и даже часто предпочтительнее, задание функции Odesolve (t, t1, step) с тремя параметрами, где step— внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге — Купы, будет рассчитывать решение дифференциального уравнения. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск. Помните, что подбором этого параметра можно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Пример решения задачи Коши для ОДУ первого порядка у’ =у-у 2 посредством вычислительного блока приведен в листинге 11.1.

Листинг 11.1. Решение задачи Коши для ОДУ первого порядка

Не забывайте о том, что вставлять логические операторы следует при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры помните, что логическому знаку равенства соответствует сочетание клавиш + . Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано в листинге 11.1, так и в виде штриха, набрав его с помощью сочетания клавиш + (соответствующий пример будет приведен ниже в листинге 11.3.) Выбирайте тот или иной способ представления производной из соображений наглядности представления результатов — на ход расчетов он не влияет.

Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге-Кутты. Для смены метода необходимо нажатием правой кнопки мыши на области функции odesolve вызвать контекстное меню и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг) или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е. метод Рунге — Кутты с фиксированным шагом. Подробнее о различии этих методов сказано в разд. 11.3.

1. Электромагнитная волна (в религиозной терминологии релятивизма — «свет») имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например,

200 тыс км/с в стекле и

3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью «Температура эфира и красные смещения»), разную скорость для разных частот (см. статью «О скорости ЭМ-волн»)

2. В релятивизме «свет» есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский «свет» — это волнение ничего в ничем. У него нет среды-носителя колебаний.

3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.

4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те «подтверждающие теорию Эйнштейна факты», которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.