«Решение систем линейных уравнений»
презентация к уроку по алгебре (7 класс) на тему
3 презентации к урокам
Скачать:
| Вложение | Размер |
|---|---|
| Решение систем линейных уравнений. Метод подстановки | 391.5 КБ |
| Решение систем линейных уравнений. Метод сложения | 485.5 КБ |
| Решение систем линейных уравнений. Графический метод | 559.5 КБ |
Предварительный просмотр:
Подписи к слайдам:
Предварительный просмотр:
Подписи к слайдам:
Предварительный просмотр:
Подписи к слайдам:
Решение систем линейных уравнений Алгебра (7 класс) Учитель математики Васютина Е.Г. Гимназия Альма Матер
Графический способ решения систем линейных уравнений
Дана система линейных уравнений Рассмотрим каждое уравнение в отдельности. Геометрической иллюстрацией уравнения с двумя неизвестными служит его график на координатной плоскости.
Дана система линейных уравнений Рассмотрим первое уравнение Выразим из этого уравнения y через x .
Поэтому графиком данного уравнения является прямая. Данное уравнение можно рассматривать как формулу, задающую линейную функцию. Для построения графика найдем две точки. 1) 2 )
Вернемся к системе линейных уравнений Рассмотрим второе уравнение Выразим из этого уравнения y через x .
Поэтому графиком данного уравнения является прямая. Данное уравнение также как и первое можно рассматривать как формулу, задающую линейную функцию. Для построения графика найдем две точки. 1) 2 )
Построим график второй функции
Найдем координаты точки пересечения прямых
Координаты точки пересечения прямых ― это решение системы В этом случае говорят, что система решена графически
Для графического решения системы нужно: Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных прямых (если они пересекаются)
Однако при графическом способе решения системы уравнений обычно получается приближенное решение
Но На плоскости возможны три случая взаимного расположения двух прямых ― графиков уравнений системы
Три случая взаимного расположения двух прямых 1. Прямые пересекаются. То есть имеют одну общую точку. Тогда система уравнений имеет единственное решение. Например, как в рассмотренной системе
Три случая взаимного расположения двух прямых 2. Прямые параллельны. То есть не имеют общих точек. Тогда система уравнений решений не имеет. Например:
Три случая взаимного расположения двух прямых 3. Прямые совпадают. Тогда система уравнений имеет бесконечно много решений. Например:
Решите графически следующие системы уравнений
Подберите, если возможно такое значение m , при котором система имеет а) единственное решение б) не имеет решений в) имеет бесконечное множество решений
Подберите, если возможно такое значение m , при котором система имеет а) единственное решение б) не имеет решений в) имеет бесконечное множество решений
Подберите, если возможно такое значение m , при котором система имеет а) единственное решение б) не имеет решений в) имеет бесконечное множество решений
Графический способ решения систем линейных уравнений Домашнее задание: № 642 (1,3); № 644-646(1)
Урок закончен. Спасибо. До встречи на следующем уроке!
Презентация на тему «Способы решения систем уравнений»
Данная презентация разработана для учащихся 9х классов, с целью систематизации знаний, отработки навыков решения систем способом подстановки, сложения, графическим методом, методом введения новых переменных. Материал интересен для повторения в период подготовки к ГИА. Материал дополнен историческими данными.
«Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях» Б.В.Гнеденко
Просмотр содержимого документа
«Презентация на тему «Способы решения систем уравнений» »
Способы решения систем уравнений
Кудряшова Любовь Александровна, учитель математики.
МОУ СОШ № 9г. Переславль-Залесский, 2010 г
Рассмотреть различные способы решения систем уравнений
Из истории решения системы уравнений
В древневавилонских текстах, написанных в III — II тысячелетиях до н. э., содержится немало задач, решаемых с помощью составления систем уравнений. Например: «Площади двух своих квадратов я сложил: Сторона второго квадрата равна стороны первого
Соответствующая система уравнений в современной записи имеет вид:
Хотя вавилоняне и не имели алгебраической
символики, они решали задачи алгебраическим
Из истории решения системы уравнений
Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения.
«Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208»
Различные способы решения систем уравнений
- метод подстановки
- метод сложения
- метод введения новых переменных
- графический метод
- Одно из уравнений системы преобразуют к виду, в которомyвыражено через х ( или х черезy)
- Полученное выражение подставляют вместоy(или вместо х ) во второе уравнение. В результате получается уравнение с одной переменной
- Находят корни этого уравнения
- Воспользовавшись выражениемyчерез х(или х черезy), находят соответствующие значения х (илиy)
- Преобразовать коэффициенты так, чтобы коэффициенты при х или у были противоположными числами
- Сложить получившиеся уравнения
- Решить уравнение с одной переменной
Метод введения новых переменных
- Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми.
- Реши полученную систему уравнений методам наиболее подходящим для э той системы уравнений.
- Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.
- Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.
- Выразить в обоих уравнениях системы переменнуюучерез переменнуюх
- Построить графики функций в однойсистеме координат.
- Отметить точки пересечения графиков, выписать их координаты.
- Записать в ответ полученные пары
Решить систему уравнений:
-3,-1,1,3 отличны от нуля, значит, они являются корнями уравнения:
Решить систему уравнений:
Умножу первое уравнение системы на число 2,
а второе на число -3, получу
Сложу уравнение системы:
Подставлю найденное число вместо n в первое уравнение исходной системы:
- Система имеет одно решение: (-0,5;1)
- Ответ: ( — 0,5;1)
Преимущества и недостатки метода
- Систему уравнений легче решать методом сложения, когда коэффициенты приXиYсразу являются противоположными числами.
- Метод позволяет быстро исключить одну из неизвестных переменных и найти другую.
- Метод сложения невозможно применить,когда у переменных в двух уравнениях разные
- показатели степени.
Метод введения новых переменных
Полученные системы тоже являются симметричными системами, которые уже решали.
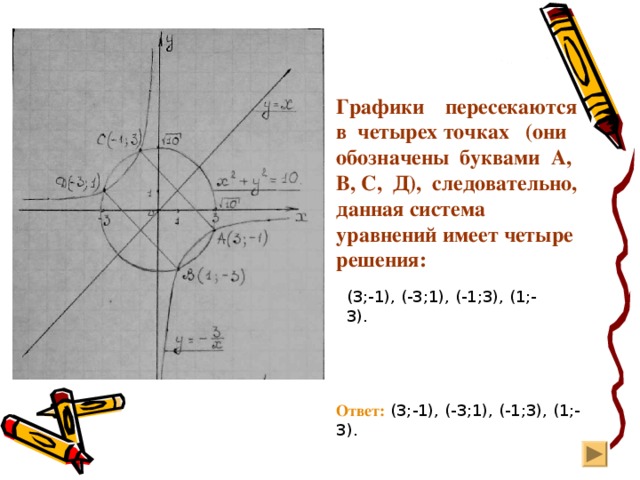
Итак, (3;1), (-1;3), (-3;1),(1;-3) — решения данной системы.
В одной системе координат построим графики уравнений: ху= -3 и
Г рафиком уравнения ху=-3 является гипербола, в етви которой расположены во II и IV координатных четвертях.
Г рафиком уравнения является окружность с центром в точке (0;0) и радиусом
Графики пересекаются в четырех точках (они обозначены буквами А, В, С, Д), следовательно, данная система уравнений имеет четыре решения:
Преимущества и недостатки метода
Графический метод решения систем , как и графический метод решения уравнений , красив , но ненадежен :
- во-первых,потому,что графики уравнений мы сумеем построить далеко не всегда;
- во-вторых,даже если графики уравнений удалось построить,точки пересечения могут быть не такими «хорошими»,как в специально подобранных примерах учебника, а то и вовсе могут оказаться за пределами чертежа.
- Реши систему уравнений, используя метод подстановки:
- Реши систему уравнений, используя метод сложения:
- Реши систему уравнений , используя графический способ:
- Реши систему уравнений, используя метод подстановки:
Мы рассмотрели четыре различных способов решения систем уравнений. Каждый выберет для себя способ, который ему больше всего понравился, самое главное — что каждый из Вас научился решать системы такого вида и поэтому эпиграфом могли служить слова Б.В.Гнеденко:
«Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях»
Кафедра математики и моделирования Старший преподаватель Е.Г. Гусев Курс «Высшая математика» Лекция 3. Тема: Системы линейных уравнений: методы решения. — презентация
Презентация была опубликована 6 лет назад пользователемМарина Городенская
Похожие презентации
Презентация на тему: » Кафедра математики и моделирования Старший преподаватель Е.Г. Гусев Курс «Высшая математика» Лекция 3. Тема: Системы линейных уравнений: методы решения.» — Транскрипт:
1 Кафедра математики и моделирования Старший преподаватель Е.Г. Гусев Курс «Высшая математика» Лекция 3. Тема: Системы линейных уравнений: методы решения. Цель: Рассмотреть понятие СЛАУ.
2 Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: Здесь x 1, x 2,, x n – неизвестные величины; a ij (i = 1,2, …, m; j =1,2, …, n) – числа, называемые коэффициентами системы (первый индекс — номер уравнения, второй номер неизвестной); b 1, b 2, …, b m – числа, называемые свободными членами.
3 Решением системы Решением системы будем называть упорядоченный набор чисел x 1, x 2, …, x n, обращающий каждое уравнение системы в верное равенство. Решитьсистему Решить систему значит найти все ее решения или доказать, что ни одного решения нет. совместной Система, имеющая решение, называется совместной.
4 Если система имеет только одно решение, то она называется определенной определенной. Система, имеющая более чем одно решение, называется неопределенной совместной неопределенной (совместной и неопределенной неопределенной). Если система не имеет решений, то несовместной она называется несовместной.
5 Система, у которой все свободные члены равны нулю (b 1 = b 2 =…= b n = 0), однородной называется однородной. Однородная система всегда совместна, так как набор из n нулей удовлетворяет любому уравнению такой системы. Если число уравнений системы совпадает с числом неизвестных (m=n), квадратной то система называется квадратной.
6 Две системы, множества решений которых совпадают, называются эквивалентными эквивалентными или равносильными. равносильными.
7 Преобразование,применение которого превращает систему в новую систему, эквивалентную исходной,называется эквивалентным равносильным эквивалентным или равносильным преобразованием. преобразованием.
8 Общий метод решения СЛАУ. (Метод Гаусса). Если система совместна, т. е. rang A = rang A* = (r),то r-уравнений СЛАУ линейно-независимы, а остальные (n — r) являются линейными комбинациями. Решить систему значит выразить базисные неизвестные через свободные, придавая различные значения свободным неизвестным.
9 Общий метод решения однородной СЛАУ. Теорема: Если ранг матрицы однородной СЛАУ = r, то система имеет (m — r) линейно — независимых решений. Опр.: Совокупность решений, т. е. совокупность называется фундаментальной системой решений однородной СЛАУ.
10 Теорема об общем решении не одноодной СЛАУ. Теорема: Если фундаментальная система решений соотв-щей однор. СЛАУ; — некоторое решение не одно. СЛАУ, то сумма — решение не одно. СЛАУ. Полученное решение называется общим решением не одноодной СЛАУ.
11 Матричный способ решения СЛАУ. СЛАУ запишем в виде А х Х=В. Если det A0, то для матрицы А сущ. обратная А-1. Умножим обе части СЛАУ слева на А-1: А-1 х А х Х = А-1 х В; Е х Х = А-1 х В; Х = А-1 х В.
12 Метод Крамера. СЛАУ имеет вид А х Х=В при det A0 ; Х=А-1 х В. х 1 A11 A12 … An1 b1 х 2 = A21 A22 … An2 х b2 = хn A1n A2n … Ann n х n bn n х 1 A1n х b1 + A2n х b2 + Ann х bn A11 х b1 + A21 х b2 ……… A12 х b1 + A22 х b2 ………
13 1. 2. Числители — величина определителя, разложенного по первому столбцу, тогда первый столбец это элементы b 1, b 2 … b n, а остальные столбцы – это столбцы матрицы А и т.д. Если det A0, то СЛАУ имеет единственное решение и определяется формулами:
14 Элементарные преобразования матрицы 1) перемена местами двух строк; 2) умножение строки на число, отличное от нуля; 3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
15 Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей треугольной матрицей. Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна определен на совместна и определенна.
16 A Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m m и стоящую справа прямоугольную матрицу, Aтрапециевидной то матрицу A назовем трапециевидной или трапецеидальной трапецеидальной.
17 Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является бесконечно неопределенной, то есть имеет бесконечно много решений много решений.
18 Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты базисными отличны от нуля), называются базисными. Остальные неизвестные называются свободными свободными.
19 Если свободным неизвестным при даны конкретные числовые значения и через них выражены базисные неизвестные, то полученное частным решение называется частным решением решением. Если свободные неизвестные выражены через параметры, то получается решение, которое общим решением. называется общим решением.
20 Если всем свободным неизвестным приданы нулевые значения, то полученное решение базисным называется базисным. Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, рангом системы называемое рангом системы.
21 Вопросы: 1)Когда система имеет единственное решение? 2)Какие элементарные преобразования матрицы можно делать при решении СЛАУ?
http://kopilkaurokov.ru/matematika/presentacii/priezientatsiia-na-tiemu-sposoby-rieshieniia-sistiem-uravnienii
http://www.myshared.ru/slide/1246262/