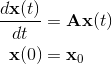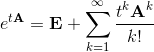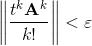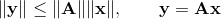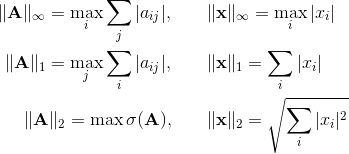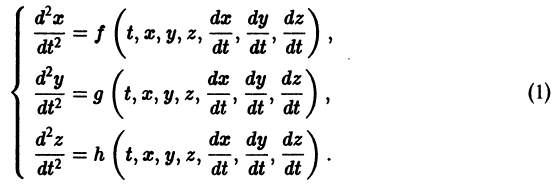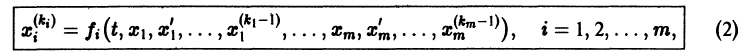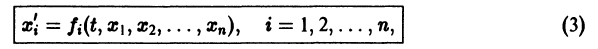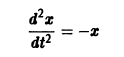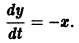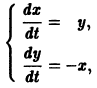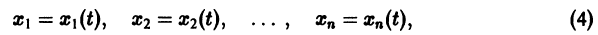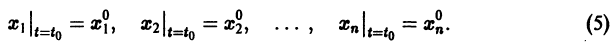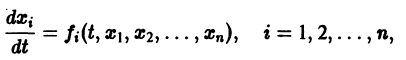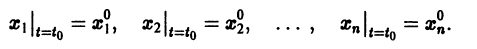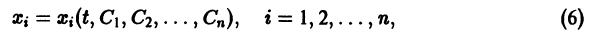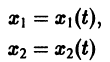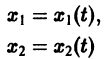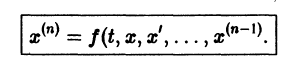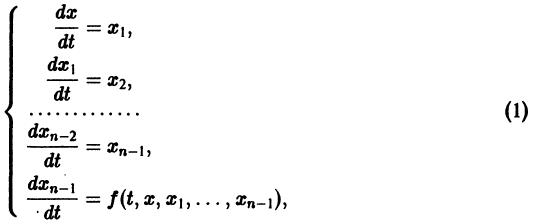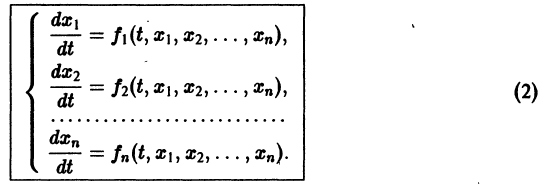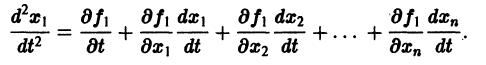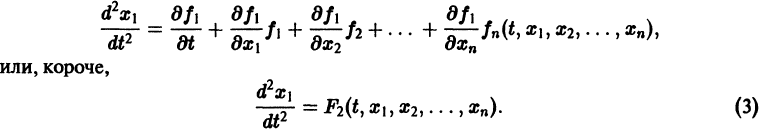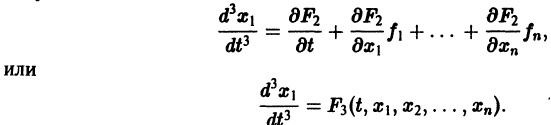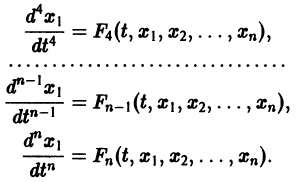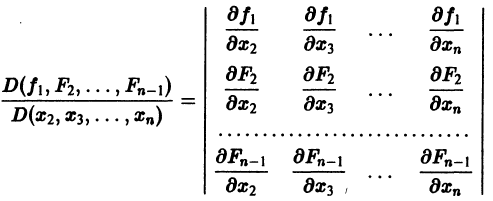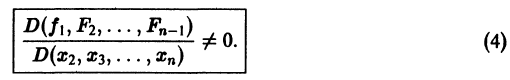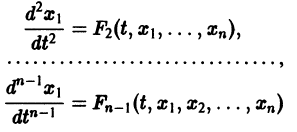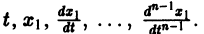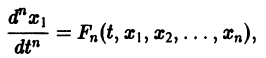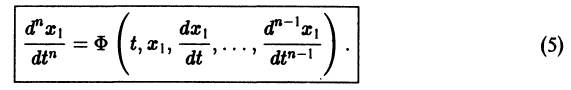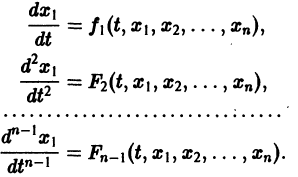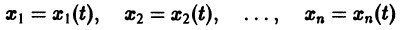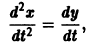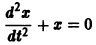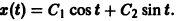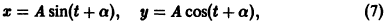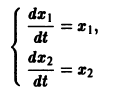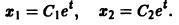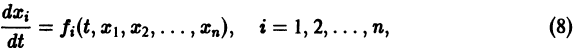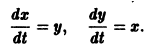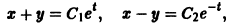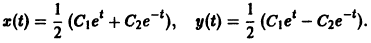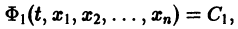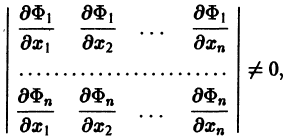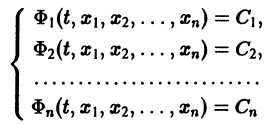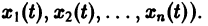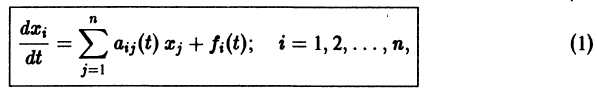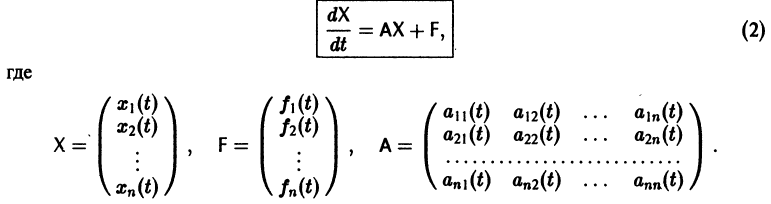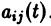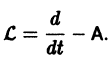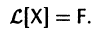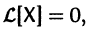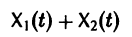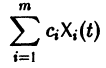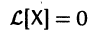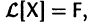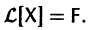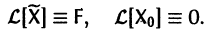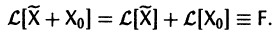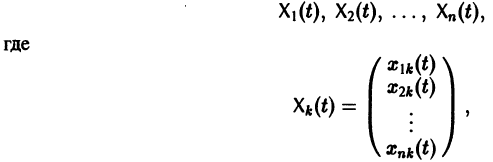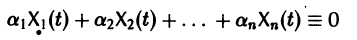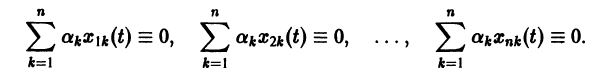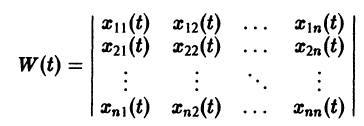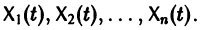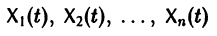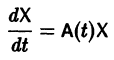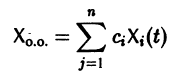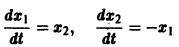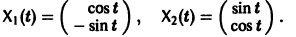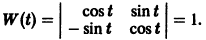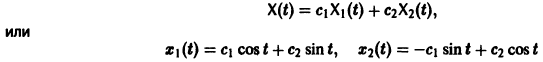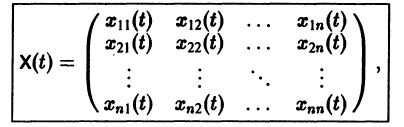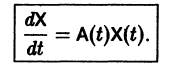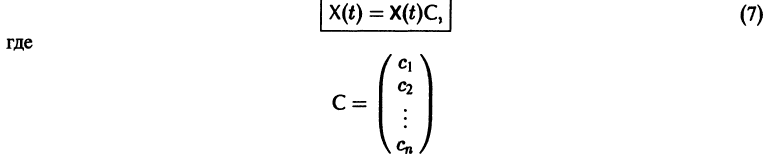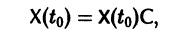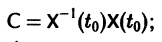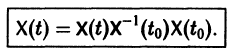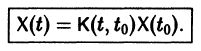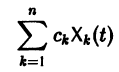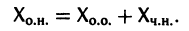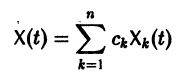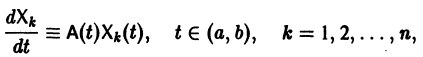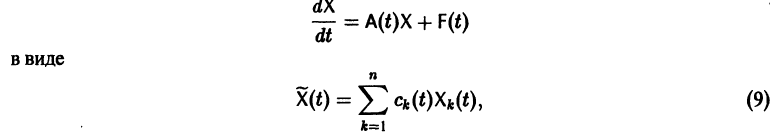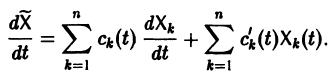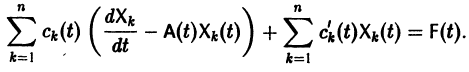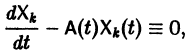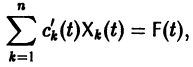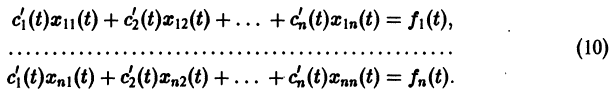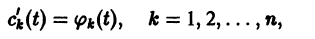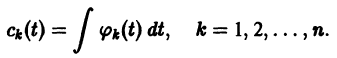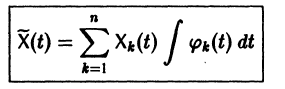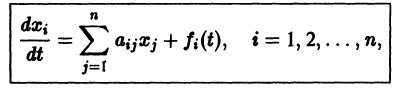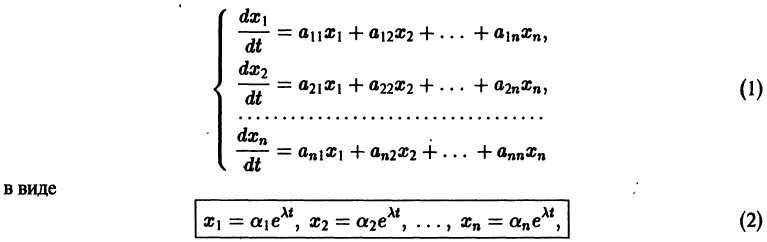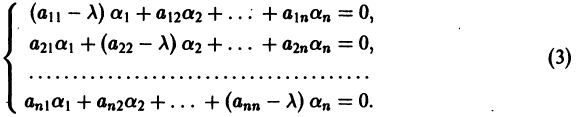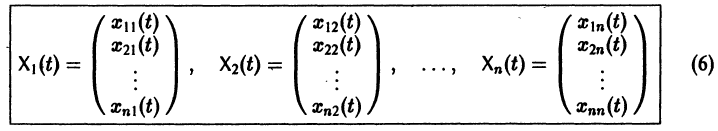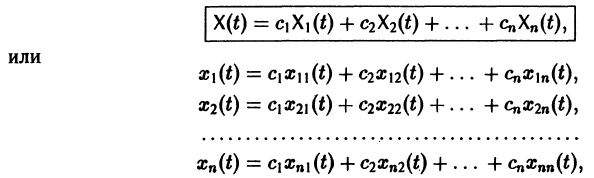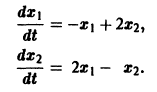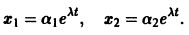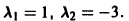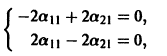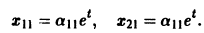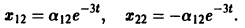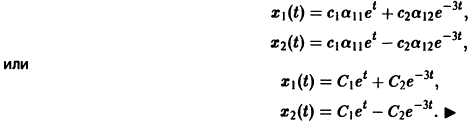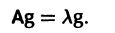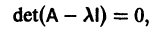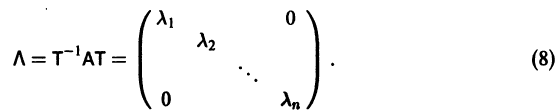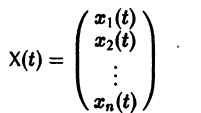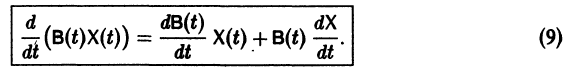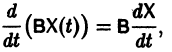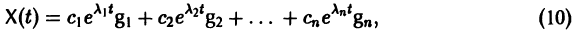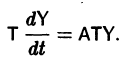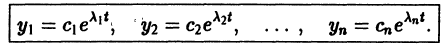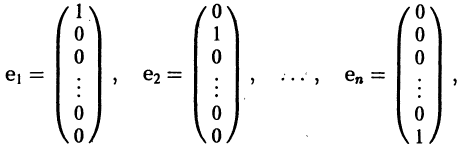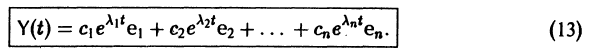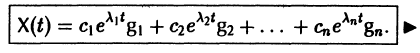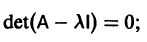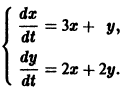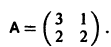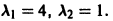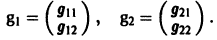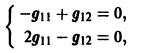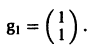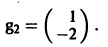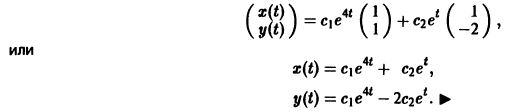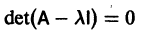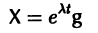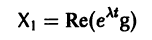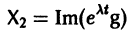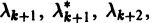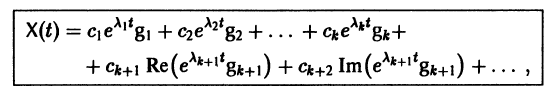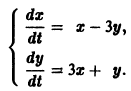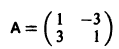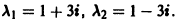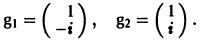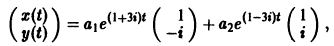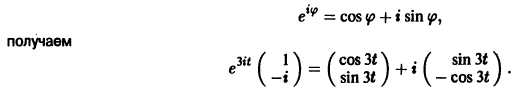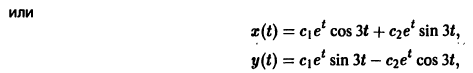Решение систем дифференциальных уравнений матричным способом
Вы будете перенаправлены на Автор24
Матричная запись системы обыкновенных дифференциальных уравнений (СОДУ) с постоянными коэффициентами
Линейную однородную СОДУ с постоянными коэффициентами $\left\<\begin
где $y_ <1>\left(x\right),\; y_ <2>\left(x\right),\; \ldots ,\; y_
Теперь на основе правила умножения матриц данную СОДУ можно записать в виде матричного уравнения $\frac
Общий метод решения СОДУ с постоянными коэффициентами
Решение СОДУ отыскивается в следующем виде: $y_ <1>=\alpha _ <1>\cdot e^
Теперь матричному уравнению данной СОДУ можно придать вид:
Полученное уравнение можно представить так:
Последнее равенство показывает, что вектор $\alpha $ с помощью матрицы $A$ преобразуется в параллельный ему вектор $k\cdot \alpha $. Это значит, что вектор $\alpha $ является собственным вектором матрицы $A$, соответствующий собственному значению $k$.
Готовые работы на аналогичную тему
Это уравнение называется характеристическим.
Одно из значений в этой матрице выбирают произвольно.
Окончательно, решение данной системы в матричной форме записывается следующим образом:
где $C_ $ — произвольные постоянные.
Записываем матрицу системы: $A=\left(\begin
Получаем характеристическое уравнение:
Корни характеристического уравнения: $k_ <1>=1$, $k_ <2>=9$.
Получаем решение СОДУ в матричной форме:
В обычной форме решение СОДУ имеет вид: $\left\<\begin
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 01 2022
Как не стоит вычислять матричную экспоненту
Пост написан под влиянием поста пользователя pchelintsev_an.
В данной статье я постараюсь рассказать, с какими вычислительными трудностями можно столкнуться, если пойти по «наивному» пути вычисления матричной экспоненты. Статья может быть полезна тем, кто хотел бы познакомиться с вычислительной математикой, но уже знаком с такими понятиями как система обыкновенных дифференциальных уравнений и задача Коши. Эксперименты проводились с использованием системы GNU Octave.
Что вообще такое матричная экспонента и для чего она применятеся
Матричная экспонента возникает при рассмотрении задачи Коши для линейной системы обыкновенных дифференциальных уравнений с постоянными коэффициентами:
Иногда такие системы возникают после частичной дискретизации уравнений в частных производных, например, в методах конечных элементов. Тогда матрица A является некоторой конечномерной аппроксимацией дифференциального оператора. Как следствие, число строк матрицы A может легко достигать тысяч, миллионов и даже нескольких миллиардов. Такие матрицы даже невозможно хранить в виде квадратного массива, поэтому их хранят в специальных разреженных форматах представления.
Решение системы ОДУ можно выписать явно:
Здесь появляется матричная экспонента, которая определяется как сумма ряда:
Фактически, матричная экспонента получается формальной подстановкой матрицы A в ряд Тейлора для e z (Математик отметит, что ряд сходится абсолютно для любой матрицы и любого t). Удобно то, что с помощью матричной экспоненты можно вычислить решение в любой момент времени t. Например, если эту систему решать каким-нибудь методом численного интегрирования, например, Адамса или Рунге-Кутты, то затраченное время будет пропорционально времени t. Однако, решение через матричную экспоненту возможно лишь для автономных систем с постоянными коэффициентами.
В курсе дифференциальных уравнений для практических вычислений матричной экспоненты предлагается метод приведения матрицы к жордановой форме: если матрицу A представить в виде S J S -1 , где J – жоржанова форма, S – матрица перехода к жорданову базису, то матричная экспонента А выражается через матричную экспоненту J:
Матричная экспонента от жордановой матрицы J выписывается в явном виде. Однако такой способ требует вычисления системы собственных векторов, а также присоединенных к ним векторов. Эта задача значительно сложнее исходной. К тому же, даже для действительной матрицы А, ее жорданова форма J может быть комплексной.
Суммирование ряда
Итак, у нас есть бесконечный ряд и желание вычислить его за обозримое время. Очевидный путь – закончить суммирование на каком-то слагаемом, отбросив остаток. При этом суммирование ряда заканчивается, если очередное k-е слагаемое по норме мало:
Нормы матрицы
Остановимся ненадолго на норме матрицы. Различных норм матрицы существует достаточно много. Можно ввести норму, исходя из требования
В этом случае говорят о норме матрицы индуцированной (или подчиненной) некоторой векторной норме. Для наиболее употребимых векторных норм соответствующие матричные нормы имеют вид:
Первые две нормы матрицы считаются элементарно, а для последней требуется вычислить сингулярное число, что весьма непросто. Кроме индуцированных норм существует еще ряд других норм. Практически удобной является норма Фробениуса, которая, с одной стороны, легко вычисляется, а с другой – тесно связана с сингулярными числами А. Фактически, это евклидова норма вектора, полученного «вытягиванием» матрицы в одну строку:
Сюрпризы при суммировании ряда
Чтобы осознать сложности, возникающие при суммировании рядов Тейлора, не обязательно обращаться к примеру с матричной экспонентой. Попробуем просто построить график функции e -x на отрезке [0, 50], суммируя аналогичным образом ряд Тейлора для экспоненты. Суммирование завершим, если очередное слагаемое не превосходит 10 -20 . Воспользуемся следующим кодом на Octave:
Результат получается довольно странным:
При x > 30 график функции начинает вести себя хаотично и не имеет с экспонентой ничего общего.
Причина данного эффекта в накоплении погрешностей округления. Например, при вычислении e -35 было просуммировано 132 слагаемых, из которых минимум абсолютной величины имело последнее слагаемое s132 ≈ 5.8674 · 10 -21 , а максимум абсолютной величины имело слагаемое с номером 35: s35 ≈ -1.067 · 10 14 . Поскольку Octave проводит вычисления с двойной точностью (примерно 16 значащих цифр), округление 35-го слагаемого уже внесло ошибку порядка 0.01, что существенно превосходит и значение ϵ = 10 -20 и само значение суммы ряда e -35 ≈ 6.305 · 10 -16
Неужели ряд Тейлора настолько безнадежен? Нет, ошибки округления не будут давать существенного вклада, если величина суммируемых слагаемых не будет достигать таких огромных значений. Например, такой алгоритм будет надежно работать при небольших значениях x (|x| ≲ 1). Для матричной экспоненты аналогичное условие имеет вид . Кроме вычислительной устойчивости такой выбор x обеспечивает быструю сходимость, то есть достаточно взять всего несколько слагаемых из ряда для получения приемлемой точности.
Метод удвоения аргумента
Заметим, что матричная экспонента удовлетворяет следующему соотношению:
Это означает, что матричную экспоненту можно посчитать для матрицы , а затем возвести результат в степень N. Взяв в качестве N = 2 p можно воспользоваться быстрым алгоритмом возведения в степень за p матричных умножений:
- Вычислить матричную экспоненту
- Умножить B на себя
, повторив эту операцию p раз
- В результате,
Число p можно (и нужно) выбрать из соображений вычислительной устойчивости шага 1 алгоритма, то есть
Соответствующий Octave код:
Метод аппроксимаций Паде
Отрезок ряда Тейлора – не единственный способ приближенно вычислить значение функции. Более качественные приближения функции могут быть получены не в виде многочленов, а в виде рациональных функций. Наилучшие приближения в виде отношения двух многочленов заданных степеней называются аппроксимациями Паде. Например, аппроксимация Паде отношением двух квадратичных многочленов для экспоненты записывается в виде:
Аналогичная аппроксимация для матричной экспоненты будет иметь вид:
Аппроксимации Паде могут использоваться для шага 1 в алгоритме удвоения. Основная сложность, связанная с аппроксимациями Паде, заключается в необходимости один раз обратить матрицу. Для больших матриц это может быть довольно трудозатратно.
Анализ точности
Как убедиться, что матричная экспонента вычислена правильно? Достаточно ли, что или требуется более «интеллектуальная» проверка?
Вспомним, что матричная экспонента возникла не на ровном месте, а в результате решения некоторой системы обыкновенных дифференциальных уравнений. Собственные числа матрицы A характеризуют скорости процессов, протекающих в системе, описываемой данной системой дифференциальных уравнений. Например, матрица:
описывает систему с одним быстро затухающим процессом (собственное значение -1000) и двумя колебательными процессами (собственные значения ±i). Хорошим критерием правильности вычисления матричной экспоненты может являться соотношение:
связывающее собственные значения матрицы A и ее матричной экспоненты.
Вычислительный эксперимент
Для начала исследуем алгоритмы на быстродействие на случайных матрицах разного размера. В качестве методов используем метод суммирования ряда Тейлора, метод удвоения аргумента и встроенную в Octave функцию expm. Изначально хотелось сравнить также соответствие собственных значений, но от этой идеи пришлось отказаться, поскольку все три алгоритма одинаково проваливали эту проверку при размерах матрицы N ≳ 50. Возможно виновником этого была функция определения собственных значений eig, работающая недостаточно точно или плохая обусловленность самой задачи определения собственных значений для этих матриц.
Исходя из графика, метод удвоения работает примерно вдвое дольше библиотечной функции (возможно стоит ослабить завышенное требование по точности), в то время как прямое суммирование имеет даже иную асимптотику ≈O(N 3.7 ), в то время, как остальные имеют асимптотику O(N 3 ).
Далее, проверим как алгоритм работает с большими по величине собственными значениями. Рассмотрим следующую систему обыкновенных дифференциальных уравнений:
С начальным условием:
.
Её особенность в том, что одно из ее собственных значений равно -1000 (быстро затухающее решение), а два других равны ±i√2 (колебательные решения). Если в мнимые собственные значения будут внесены искажения, это будет хорошо заметно. Возьмем шаг по времени τ = 0.038, найдем матричную экспоненту разными способами. Решение системы на сетке с шагом τ получается следующим простым алгоритмом:
- Решение в начальный момент известно из начального условия
- Зная решение un в момент tn, решение в момент tn+1 = tn + τ получается из него умножением на матричную экспоненту B:
Посмотрим на полученные численные траектории (отображена только первая компонента вектора):
Все траектории, кроме полученной с помощью прямого суммирования ряда Тейлора, визуально совпадают. Обратите внимание, график не выходит из начального условия x1(0) = 1. На самом деле, график экспоненциально подходит к точке y = 1, просто характерное расстояние «поворота» графика (∼ 1 / 1000) намного меньше шага по времени τ = 0.038.
Можно сказать, что пример синтетический, и на практике не встретится, однако это не так. Существует множество так называемых жестких задач Коши, которые характеризуются сильным разбросом собственных значений (по сути, скоростей физических процессов).
Дальнейшее чтение
О различных способах вычисления матричной экспоненты можно почитать в статье (англ.) [2]. По методам решения обыкновенных дифференциальных уравнений и жестких задач написан замечательный двухтомник [3,4]
Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 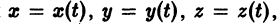
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 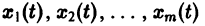
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 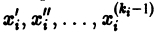
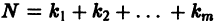
Например, одно уравнение
является мастным случаем канонической системы. Положив 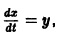
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 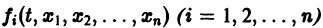
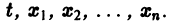

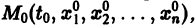

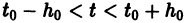
Определение:
Система n функций
зависящих от t и n произвольных постоянных 

1) при любых допустимых значениях 
2) в области 
Решения, получающиеся из общего при конкретных значениях постоянных 
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 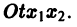
системы (7), принимающее при 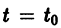
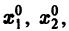
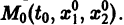
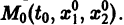
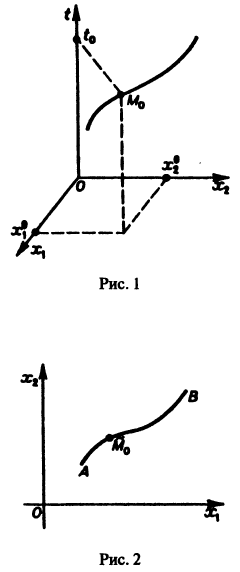
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 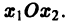
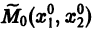
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 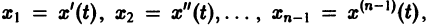
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 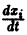
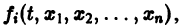
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 

Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 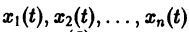
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 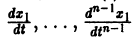
от t в систему уравнений
По предположению эту систему можно разрешить относительно 

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
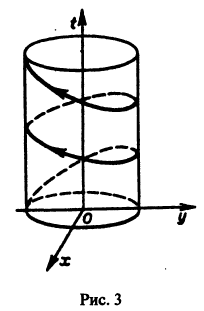
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 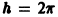
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 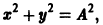
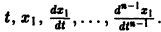
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
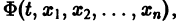
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 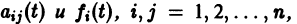
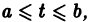
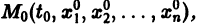
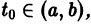
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
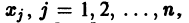
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 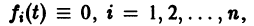
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 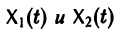
Следствие:
с произвольными постоянными коэффициентами сi решений 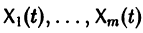
является решением той же системы.
Теорема:
Если 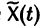
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 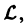
Это означает, что сумма 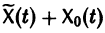
Определение:
называются линейно зависимыми на интервале a
при 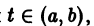

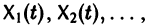
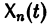
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 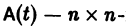
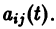
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 
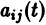
(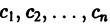
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 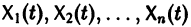
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 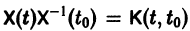
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 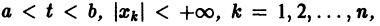
с непрерывными на отрезке 
соответствующей однородной системы и какого-нибудь частного решения 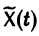
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 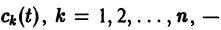
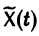
Подставляя 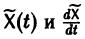
то для определения 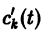
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 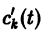
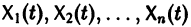
где 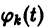
Подставляя эти значения 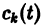
(здесь под символом 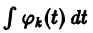
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 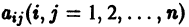
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 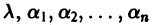
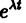
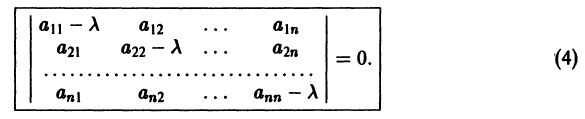
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 


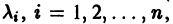
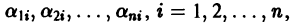
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 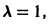
откуда а21 = а11. Следовательно,
Полагая в 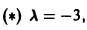
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

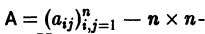
Напомним некоторые понятия из линейной алгебры. Вектор 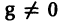
Число 
где I — единичная матрица.
Будем предполагать, что все собственные значения 
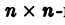
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 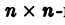








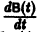
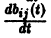
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 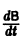
Теорема:
Если собственные значения 
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
Умножая обе части последнего соотношения слева на 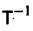
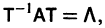
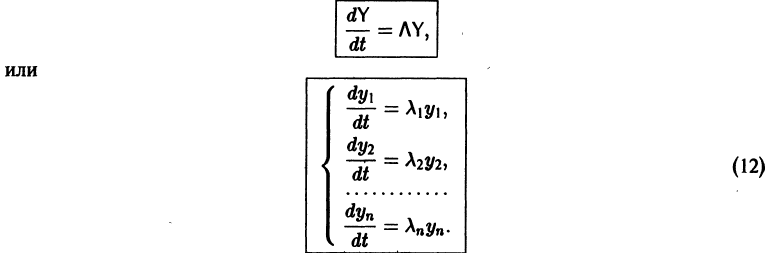
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 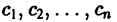
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 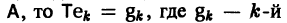
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 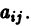
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 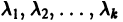
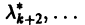
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
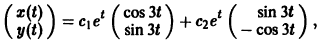
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений



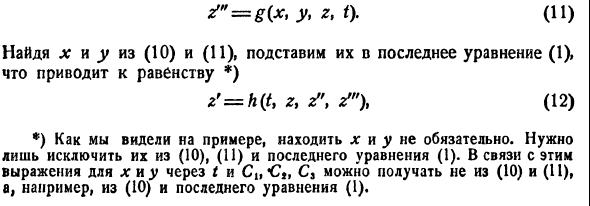

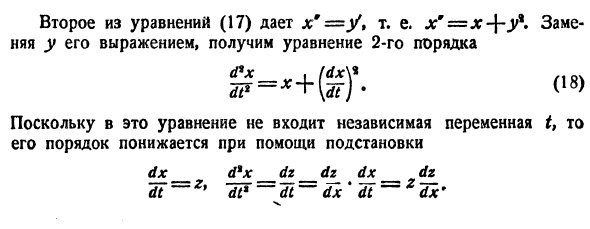

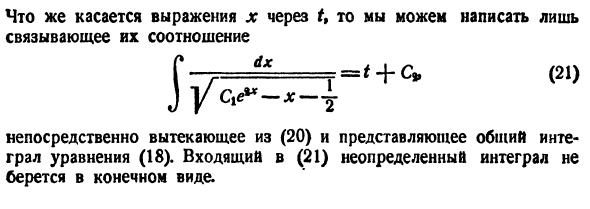

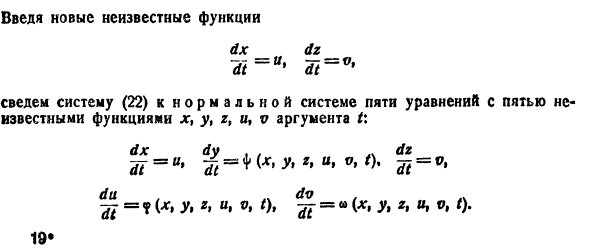
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://habr.com/ru/post/239303/
http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/