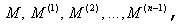Решение системы линейных уравнений метод халецкого

Метод главных элементов.

Сумы 2006

Содержание

Постановка задачи

2. Точные методы решения СЛАУ

3. Практическая реализация метода Халецкого

3.1 Программа на языке Pascal

3.2 Решение в Excel

Решить систему линейных алгебраических уравнений, используя точный метод численного решения (схему Халецкого).

Введение

Существует несколько способов решения таких систем, которые в основном делятся на два типа: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы, 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов.

Для того чтобы система линейных алгебраических уравнений имела решение, необходимо и достаточно, чтобы ранг основной матрицы был равен рангу расширенной матрицы. Если ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных, то система имеет единственное решение. Если ранг основной матрицы равен рангу расширенной матрицы, но меньший числа неизвестных, то система имеет бесконечно решений.

Пример системы линейных уравнений:

Или в матричном виде: ,

где матрица коэффициентов системы;

— вектор неизвестных; — вектор свободных членов.

Точные методы решения СЛАУ

Метод главных элементов.

Пусть дана система линейных алгебраических уравнений. Рассмотрим расширенную матрицу, состоящую из коэффициентов системы a[i,j] и свободных членов b[i]. Метод главных элементов — это обобщение метода исключения переменных (метода Гаусса). Обозначим матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов исходной системы за M.

Выбираем наибольший по модулю элемент, не принадлежащий столбцу свободных членов. Пусть это будет 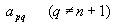. Этот элемент называется главным элементом, а строка, в которой он находится, называется главной строкой.

Далее производим следующие преобразования: к каждой неглавной строке прибавим главную строку, умноженную на соответствующий множитель для этой строки. В результате мы получим матрицу, у которой q-й столбец состоит из нулей. Отбросим этот столбец и главную p-ю строку, получим новую матрицу с меньшим на единицу числом строк и столбцов. Над матрицей повторяем те же операции, после чего получаем матрицу и т.д. Таким образом, мы построим последовательность матриц

последняя, из которых представляет двучленную матрицу — строку, её также будем считать главной строкой. Для определения неизвестных объединяем в систему все главные строки, начиная с последней. После надлежащего изменения нумерации неизвестных получается система с треугольной матрицей, из которой легко шаг за шагом найти неизвестные данной системы.

Заметим, что метод Гаусса является частным случаем, метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. Запрограммировать метод главных элементов непросто, поэтому чтобы уменьшить вычислительную погрешность, применяют метод Гаусса с выбором главного элемента. Необходимое условие применения метода главных элементов: определитель системы не равен нулю.

Разложение матриц на треугольные множители. Схема Холецкого

Лекция 3. Метод Холецкого

Метод Гаусса, подробно рассмотренный выше, был и остается основным инструментом для решения систем линейных уравнений. Основным, но не единственным. Нам следует получить представление еще о двух группах методов: 1) методы разложения матрицы на треугольные множители; 2) итерационные методы.

Рассмотрим метод Холецкого, который предназначен для решения систем с симметричными положительно определенными матрицами. Почему нас интересуют именно такие матрицы?

Во-первых, как известно, матрица жесткости (см (1.1)) является симметричной матрицей.

Во-вторых, вспомним, что при использовании метода конечных элементов потенциальная энергия конструкции определяется выражением

, (3.1)

где q – вектор перемещений конструкции, а K – ее матрица жесткости.

Аналогично, для кинетической энергии системы получено

, (3.2)

где M – матрица инерции.

В исходном, недеформированном, состоянии потенциальная энергия деформации конструкции равна нулю. В то же время любые перемещения точек конструкции приводят к ее деформации и, значит, к увеличению П по сравнению с недеформированным состоянием. Таким образом, исходя только из соображений физического смысла, мы пришли к выводу о положительной определенности матрицы жесткости. Подобные соображения можно привести и для матрицы инерции.

Теорема Холецкого. Если A – симметричная положительно определенная матрица, то существует действительная невырожденная нижняя треугольная матрица L такая, что , т.е.

Согласно этой теореме мы можем заменить в исходной системе линейных уравнений матрицу на ее разложение:

. (4)

Если мы обозначим , то можем легко решить задачу в два этапа:

1) — определяем y;

2) — определяем x.

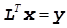
Обе эти системы с треугольными матрицами и, следовательно, легко решаются. То есть разложение Холецкого дает возможность заменить сложную задачу решения системы уравнений с полностью заполенной матрицей двумя простыми задачами – решение двух систем с треугольной матрицей.

Остается только научиться строить матрицу L.

Вспомним определение произведения матриц: . Следовательно, элемент есть произведение i-й строки матрицы L на j-й столбец матрицы :

. (3.5)

Учтем симметричность матрицы A. Это значит, что мы можем ограничиться рассмотрением только элементов нижнего треугольника матрицы A :

. (3.6)

Теперь для получения удобных для использования формул полезно записать это выражение отдельно для поддиагональных и для диагональных элементов матрицы A:

(3.7)

Кстати, эти формулы позволяют понять, почему в теореме Холецкого содержится ограничение, которое требует положительной определенности матрицы . Если попытаться применить формулы (3.7) к матрице, не являющейся положительно определенной, то это приведет либо к получению отрицательного числа под знаком квадратного корня при вычислении , либо к некорректной операции деления на ноль при вычислении .