Решение системы показательных логарифмических уравнений неравенств

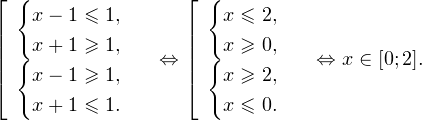
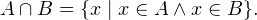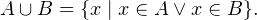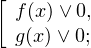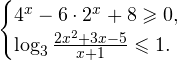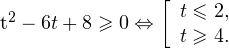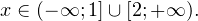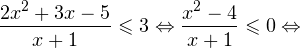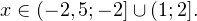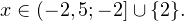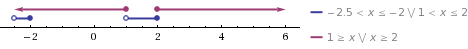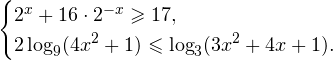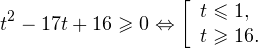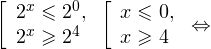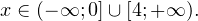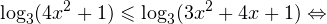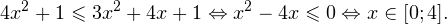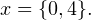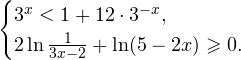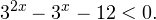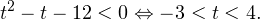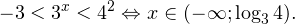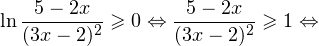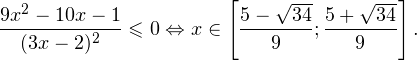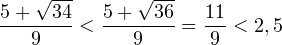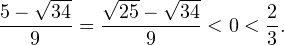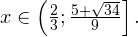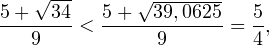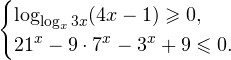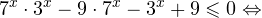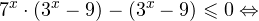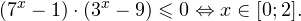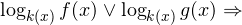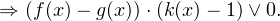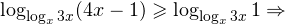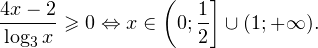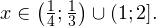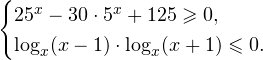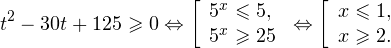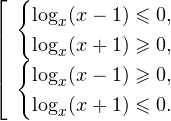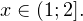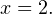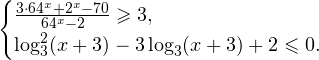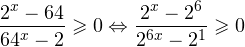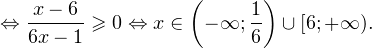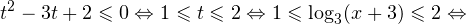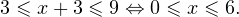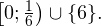Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

Опубликовано 16.09.2020Подготовка к ЕГЭ

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.

Уравнения могут быть следующих видов:

В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.

При решении уравнений нужно помнить основные термины:

— Корнем уравнения называют неизвестное число, которое нужно найти;

— Решение уравнения предполагает нахождение его корня;

— Уравнения, у которых совпадают решения называют равносильными;

— ОДЗ – область допустимых значений;

— Если возможно заменить переменные, то нужно это выполнить;

— После решения уравнения необходимо провести проверку на правильность нахождения корня.

Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.

1. Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.

Рациональным уравнением называют уравнение вида r(х)=0.

Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.

Дробно-рациональным называют уравнение, которое содержит дробное выражение.

Порядок действий при решении данного вида уравнения должен быть следующий:

— Все члены должны быть переведены в левую часть уравнения;

— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);

— Для полученного решения нужно провести проверку, то есть.

При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.

Рассмотрим ещё один пример решения рационального уравнения:

На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.

Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.

Способы решения таких уравнений:

— Возвести в степень обе части уравнения;

— Ввести новые переменные;

Пример решения уравнения по первому способу:

Пример решения по второму способу:

1. Показательные уравнения

Показательные уравнения – уравнение, содержащее неизвестный показатель.

В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.

Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).

— Уравнение с одним основанием;

— Уравнение с равными основаниями.

Существует следующие способы решения таких уравнений:

— Использовать метод логарифмов;

— Привести уравнение к квадратному виду;

— Вынести за скобку общий множитель;

— Ввести новую переменную.

Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.

Рассмотрим наиболее простой пример решения показательного уравнения:

Для решения данного уравнения следует 2 возвести во вторую степень.

Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.

Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.

Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.

Способы решения таких уравнений:

— Решение с помощью форму и приведение к простейшему;

— Ввод других переменных;

— Разложить уравнение по множителям.

Пример решения тригонометрического уравнения:

Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.

Также рассмотрим пример решения уравнения, разложив его по множителям.

Нужно применить формулу sin2x = 2sinxcosx.

2sinxcosx – sinx = 0.

sinx (2cosx – 1) = 0.

Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.

Далее, sinx=0, x=пk.

1. Логарифмические уравнения

Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.

Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.

Примерами логарифмических уравнений являются уравнения следующего вида:

Способы решения уравнений данного вида:

— Применять способ уравнивания к единице;

— Применять способ умножать на единицу;

— Применять доступные правила логарифмов;

— Введение другого основания;

— Возвести в степень.

Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.

Пример решения уравнения:

Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.

Решение уравнения является ОДЗ, то есть корень уравнения найден.

Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.

Оставить Комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Выбери тему

Самые популярные записи

• Наука. Основные особенности научного мышления. Естественные и социально гуманитарные науки (3 293)
• ЕГЭ по обществознанию: мышление и деятельность; потребности и интересы (2 238)
• Строение растения. Стебель, лист и цветок. (2 196)
• Свобода и необходимость в человеческой деятельности. Свобода и ответственность. (2 189)

StudyWay

Помощь

© 2021 StudyWay. Все права защищены.

Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».

Записаться можно через Instagram

Для этого напиши в Direct (в личку) кодовое слово «Пробный«

Что за курс и что тебя там будет ждать?

12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.

Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.

Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.

На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.

К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки

Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)

Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).

Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.

Доступ к уникальной «Академии косатиков».

Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.

Игровая система на нашей платформе StudyWay👇

За выполнение заданий получаешь баллы (XP).

При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов

Отличия тарифа «Стандарт от «Профи».

Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.

Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным

Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.

Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.

Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.

Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.

Решение систем логарифмических и показательных неравенств с репетитором

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.

Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.

1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».

2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.

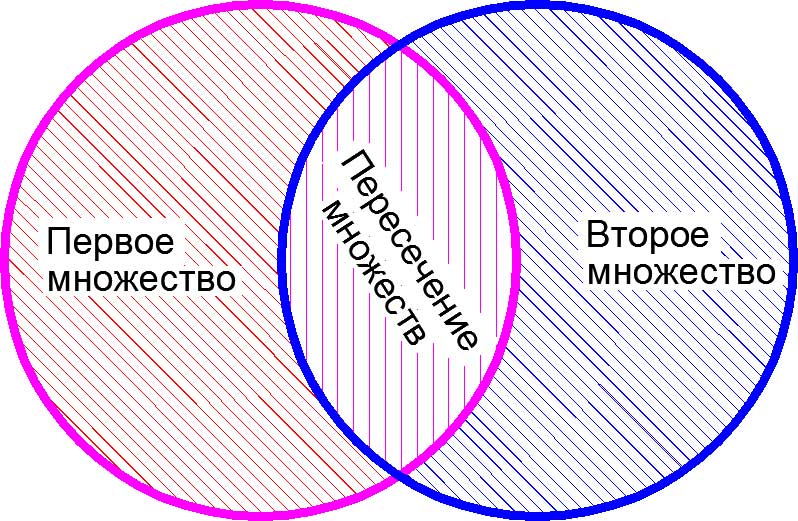
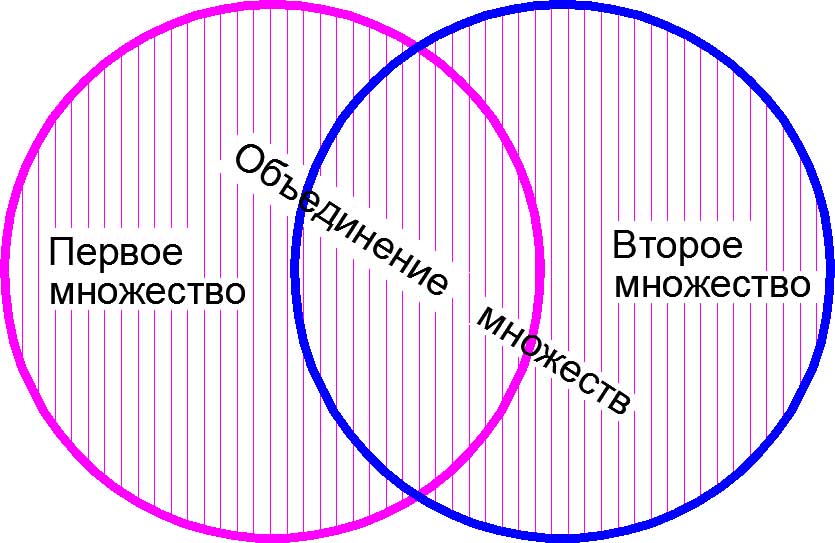
3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».

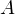
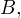
Другими словами, если даны два множества и то их пересечением будет являться множество следующего вида:

Изображение пересечения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из <ручки, карандаша, линейки, тетрадки, расчески>. У Алисы в сумочке находится «множество», состоящее из <записной книжки, карандаша, зеркальца, тетрадки, котлеты по-киевски>. Пересечением этих двух «множеств» будет «множество», состоящее из <карандаша, тетрадки>, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.

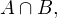
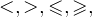
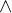
является промежуток то есть пересечение исходных промежутков. Здесь и далее под подразумевается любой из знаков ,\leqslant,\geqslant,» title=»Rendered by QuickLaTeX.com» height=»17″ width=»93″ style=»vertical-align: -4px;»/> а под — ему противоположный знак.

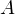
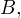
Другими словами, если даны два множества и то их объединением будет являться множество следующего вида:

Изображение объединения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из <ручки, карандаша, линейки, тетрадки, расчески, записной книжки, зеркальца, котлеты по-киевски>, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.

является промежуток 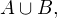то есть объединение исходных промежутков.

Перейдем непосредственно к примерам.

Решение задачи C3.

1. Решаем сперва первое неравенств. Используя замену 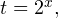переходим к неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством:

0\Leftrightarrow x\in(-2,5;-1)\cup(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

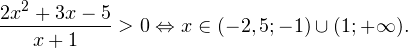
В области допустимых значений с учетом того, что основание логарифма 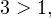1,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»52″ style=»vertical-align: -4px;»/> переходим к равносильному неравенству:

Исключая решения, не входящие в область допустимых значений, получаем промежуток

3. Ответом к системе неравенств будет пересечение полученных промежутков, то есть

Полученные промежутки на числовой прямой. Решение — их пересечение

Решение задачи C3.

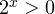
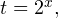
1. Решаем сперва первое неравенство. Умножаем обе части на 0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»55″ style=»vertical-align: 0px;»/> и делаем замену в результате чего приходим к неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

0, \\ 3x^2+4x+1>0\end\Leftrightarrow x\in(-\mathcal<1>;-1)\cup\left(-\frac<1><3>;+\mathcal<1>\right). \]» title=»Rendered by QuickLaTeX.com»/>

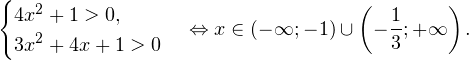
Воспользовавшись свойствами логарифмов, в области допустимых значений переходим к равносильному неравенству:

Данный промежуток целиком входит в область допустимых значений данного неравенства.

3. Общее решение системы будет являться пересечением полученных промежутков, то есть

Графическое изображение полученных промежуток. Решение системы — их пересечение

Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе его части на 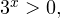0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»61″ style=»vertical-align: -4px;»/> после чего получаем неравенство:

Используя подстановку 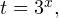переходим к следующему неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства:

0, \\ 5-2x>0 \end\Leftrightarrow \beginx>\frac<2><3>, \\ x

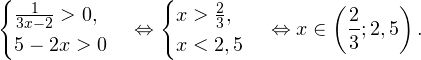
В области допустимых значений переходим к равносильному неравенству:

Обращаем внимание, что

Тогда с учетом области допустимых значений получаем:

3. Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как

\log_3\sqrt[4]<243>=\log_33^<\frac<5><4>> = \frac<5><4>, \]» title=»Rendered by QuickLaTeX.com»/>

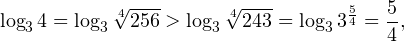
то 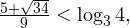и окончательный ответ к системе имеет вид:

Решение задачи С3.

1. Решим сперва второе неравенство:

2. Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства», в его основе лежит простая формула:

Вместо знака 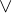может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:

Определим теперь область допустимых значений данного неравенства. Она задается следующей системой:

0, \\ \log_x 3x > 0, \\ \log_x 3x\ne 1, \\ x> 0, \\ x\ne 1\end\Leftrightarrow \beginx>\frac<1><4>, \\ \log_x 3x >\log_x 1, \\ x\ne 1, \\ x>0, \\ x\ne 1\end\Leftrightarrow \]» title=»Rendered by QuickLaTeX.com»/>

\frac<1><4>, \\ (3x-1)(x-1)>0 \\ x>0, \\ x\ne 1\end\Leftrightarrow x\in\left(\frac<1><4>;\frac<1><3>\right)\cup(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

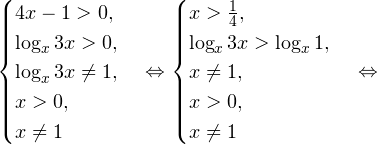
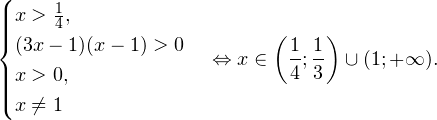
Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства.

3. Окончательным ответом исходной системы неравенств будет пересечение полученных промежутков, то есть

Решение задания C3.

1. Решаем сперва первое неравенство. Используем подстановку 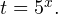Переходим к следующему квадратному неравенству:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

0, \\ x\ne 1, \\ x-1>0, \\ x+1 > 0\end\Leftrightarrow x\in(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

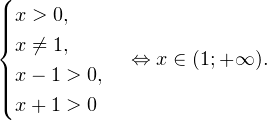
Данное неравенство равносильно следующей смешанной системе:

В области допустимых значений, то есть при 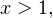1,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»53″ style=»vertical-align: -4px;»/> используя равносильные преобразования переходим к следующей смешанной системе:

С учетом области допустимых значений получаем:

3. Окончательным решением исходной системы является пересечение полученных промежутков, то есть

Изображение полученных промежутков на числовой прямой

Решение задачи C3.

1. Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду:

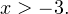
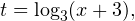
2. Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: -3.» title=»Rendered by QuickLaTeX.com» height=»14″ width=»68″ style=»vertical-align: 0px;»/> Используя замену переменной переходим к следующему квадратичному неравенству:

Этот ответ целиком принадлежит области допустимых значений неравенства.

3. Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств:

Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне.

Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека.

Логарифмические уравнения, неравенства и их системы

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

УЛЬЯНОВСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ ПРИ

УЛЬЯНОВСКОМ ГОСУДАРСТВЕННОМ ПЕДАГОГИЧЕСКОМ УНИВЕРСИТЕТЕ ИМЕНИ И.Н.УЛЬЯНОВА

КАФЕДРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ

Методы решения логарифмических

уравнений, неравенств и их систем.

УЛЬЯНОВСК 2016 г.

Цели и задачи обучения математике в школе. 3

Цели изучения алгебры и начал анализа

1. Пояснительная записка. 6

2. Программа курса. 8

3. Учебно-тематический план. 9

4. Литература. 10

5. Приложение. 12

5.1. Уравнения и неравенства. Равносильность

уравнений и неравенств. 12

5.2. Логарифмические уравнения и неравенства,

их равносильность. 13

Методы решения логарифмических

Решение систем логарифмических

Решение логарифмических неравенств. 21

Системы логарифмических неравенств. 24

Логарифмические уравнения и неравенства, содержащие переменную под знаком модуля. 25

5.8. Логарифмические уравнения и неравенства

5.9. Тексты контрольных работ. 28

Цели и задачи обучения математике в школе.

В основе характерного для нашего времени нового мировоззрения лежит представление о том, что природу нельзя «покорять», не думая о последствиях своей деятельности, что человеком нельзя управлять как машиной, и силой принуждать его к чему-либо для его же блага. Мир, в котором мы живем , является сложной саморазвивающейся динамической системой, включаю-щей в себя природу и человека. В соответствии с этим в основу школьного преподавания должны быть положены новые ценност-ные ориентиры.

Нельзя думать, что основная цель преподавания состоит только в том, чтобы сообщить ученику как можно больше конкрет-ных знаний, новых понятий, теорем, теорий. На этом пути мы приходим к разбуханию учебных программ и к тому, что значительная часть учащихся, по существу , плохо овладевает школьным материалом. Одна из важнейших целей преподавания состоит в том, чтобы воспитать молодого человека, сформировать его мировоззрение, научить его рациональному мышлению.

На уроках необходимо формировать систему ценностей, с которой молодой человек вступает в мир. Для человека, наряду с материальными ценностями, важны ценности интеллектуальные – знания, умение последовательно рассуждать, анализировать факты, обобщать их. Всему этому школьник учится на уроках математики. Решая задачи, он тренируется в точности и строгости рассуждений, учится искать различные пути выхода из создавшегося положения, привыкает преодолевать трудности. Но чтобы добиться таких результатов, нужно разъяснить ученику цели и задачи изучаемого предмета.

Математика играет важную роль в общей системе образо-вания. Важнейшей задачей обучения является обеспечение некоторого гарантированного уровня математической подго-товки всех школьников, независимо от специальности, которую они изберут в дальнейшем.

Математика, давно став языком науки и техники, в настоя-щее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требуют математической грамот-ности человека буквально на каждом рабочем месте. Это предполагает и конкретные математические знания, и определен-ный стиль мышления. Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:

— овладение конкретными математическими знаниями, необхо-димыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;

— интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;

— формирование представлений об идеях и методах матема-тики, о математике как форме описания и методе познания действительности;

— формирование представлений о математике, как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.

Цель изучения курса алгебры и начал анализа в X — XI классах — систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значений общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики. Характерной особенностью курса является системати-зация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры основной школы, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения.

Так, в курсе алгебры и начал анализа в XI классе приводятся в систему и обобщаются имеющиеся у школьников сведения о степенях, дается понятие степени с иррациональным показателем, изучаются степенная, показательная и логарифмическая функции и их свойства, кроме этого, изучаются методы решений неслож-ных иррациональных, показательных и логарифмических уравне-ний, неравенств и их систем.

В своей педагогической практике я столкнулась с тем, что при изучении логарифмов у учащихся сразу появляются затруд-нения не только в решении уравнений и неравенств, но даже само определение логарифма вызывает некоторые трудности у старшеклассников. Не сразу приходит понимание темы «Преобразования логарифмических выражений», особенно много сложностей возникает при решении логарифмических уравнений, неравенств, а тем более их систем. Большинство недочетов и ошибок встречается при проверке корней уравнения или при нахождении ОДЗ (область допустимых значений) уравнений и неравенств, ученики зачастую забывают, что проверка решения или нахождение ОДЗ является неотъемлемой частью решения уравнения или неравенства . Поэтому становится ясным, что заострять внимание школьников на этом аспекте нужно раньше, хотя бы в 8-м классе при изучении дробно-рациональных уравнений, чтобы в старших классах у учеников уже был отработан навык нахождения ОДЗ и проверки корней уравнения.

Конечно же, не все методы решения уравнений вызывают затруднения у учащихся, такие методы, как разложение на множители, введение новой переменной и сведение уравнения к квадратному, практически , несложны для старшеклассников, но метод приведения логарифмов к одному основанию вызывает сложности в восприятии и дальнейшем умении их решать.

Метод, основанный на свойстве монотонности функций, также вызывает затруднения, но это связано еще и с тем, что подобных задач очень мало в учебнике Колмогорова.

Поэтому в своей работе я сделала попытку описать наиболее часто встречающиеся методы решения логарифмических уравнений, неравенств и их систем, показала применение этих методов на примерах, которые наиболее ярко поясняют каждый выбранный метод решения. Мне кажется целесообразным разработка спецкурса по данной теме, который поможет более подробно и основательно изучить одну из самых сложных тем учебной программы по алгебре и началам анализа.

1. Пояснительная записка.

Основная цель данного спецкурса — углубление и расширение знаний учащихся по теме «Логарифмические уравнения и неравенства», повышение уровня их математической культуры, подготовка к выбору учащимися путей дальнейшего образования. Преподавание строится как углубленное изучение вопросов темы, предусмотренных программой базового уровня, так и вопросов, расширяющих кругозор, формирующих мировоззрение, раскрывающих прикладной аспект математики. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих применения высокой логической и операционной культуры, развивающих научно-теоретическое и алгоритмическое мышление учащихся. Уровень предлагаемых и решаемых задач повышенный, существенно превышающий обязательный минимум. Особое место в спецкурсе занимают задачи, требующие применения знаний в незнакомой (нестандартной) ситуации.

Особая установка спецкурса – целенаправленная подготовка учащихся к конкурсным экзаменам в ВУЗы соответствующего профиля. Поэтому преподавание спецкурса направлено на систематизацию знаний и углубление умений учащихся на повышенном уровне и на уровне, предусмотренном программой вступительных экзаменов в ВУЗы .

Основная методическая установка спецкурса – организация самостоятельной деятельности учащихся при ведущей и направляющей роли учителя. Каждый из приведенных вопросов спецкурса предусматривает возможное распределение часов. В случае необходимости, возможно изменение количества часов на изучение некоторых вопросов. Порядок изучения спецкурса определяется в соответствии с тематическим планированием базового курса, целесообразно прохождение данного спецкурса сразу после прохождения соответствующей темы базового курса алгебры и начал анализа 11 класса. Вполне допустимо, чтобы какой-то вопрос темы изучался не подряд, а перемежаясь с другими темами. При необходимости, возможно изменение содержания спецкурса, перераспределение учебного времени, придерживаясь при этом основного принципа: содержание спецкурса в первую очередь должно углублять и дополнять основной базовый курс .

Программа спецкурса состоит из следующих разделов:

— Уравнения и неравенства. Равносильность уравнений

— Логарифмические уравнения и неравенства,

— Методы решения логарифмических уравнений.

— Решение систем логарифмических уравнений.

— Решение логарифмических неравенств.

— Системы логарифмических неравенств.

— Логарифмические уравнения и неравенства, содержа-

щие переменную под знаком модуля.

— Уравнения и неравенства с параметром.

По сравнению с государственной базовой программой в спецкурс включены такие вопросы, как равносильность логарифмических уравнений и неравенств, подробно рассматривается вопрос потери корня уравнения и приобретения постороннего корня. Также включены вопросы решения уравнений с модулем и с параметром, которые в школьном учебнике « Алгебра и начала анализа» под редакцией Колмогорова А.Н. просто отсутствуют.

Данные вопросы включены в спецкурс по той причине, что уравнения и неравенства с модулем и с параметром часто встречаются на вступительных экзаменах в ВУЗы , и абитуриенты должны уметь их решать, чтобы составить достойную конкурен-цию на вступительных испытаниях.

2. Программа курса.

1. Логарифмические уравнения и неравенства, их равносильность.

Определение уравнения, неравенства, корня уравнения. Равносильность уравнений и неравенств. Определения логарифмического уравнения и неравенства. Равносильность логарифмических уравнений и неравенств. Посторонний корень, потеря корня. Формулы логарифмирования, потенцирования.

Методы решения логарифмических уравнений и их систем.

Метод потенцирования. Метод введения новой переменной. Метод логарифмирования. Функционально-графический метод. Метод введения вспомогательной переменной. Метод алгебраи-ческого сложения.

Методы решения логарифмических неравенств и их систем.

Основные теоремы. Переход от неравенства к равносильной системе неравенств. Метод введения вспомогательной переменной. Переход от старого основания логарифма к новому основанию. Метод интервалов.

Логарифмические уравнения и неравенства с модулем.

Основные приемы решения уравнений и неравенств с модулем.

Уравнения и неравенства с параметром.

Основные приемы решения уравнений и неравенств с параметром.

Обобщение и систематизация знаний по теме «Логарифмические уравнения, неравенства и их системы».