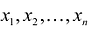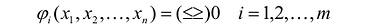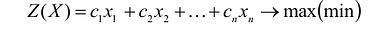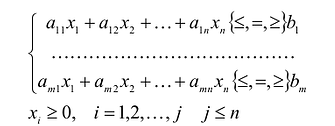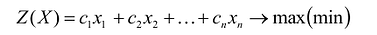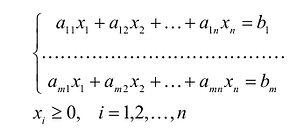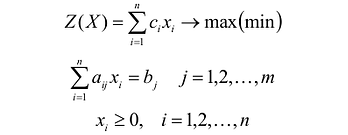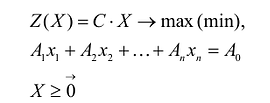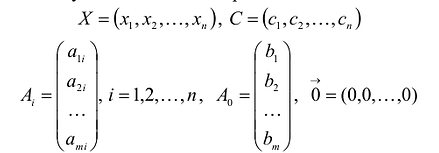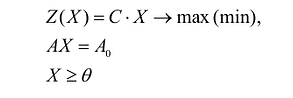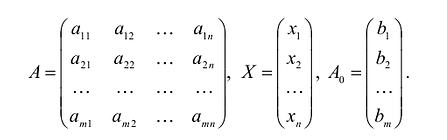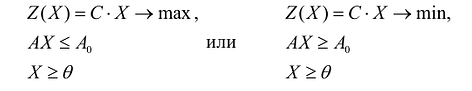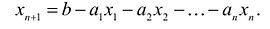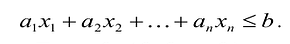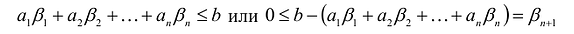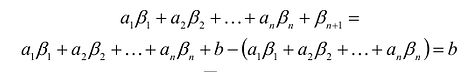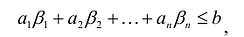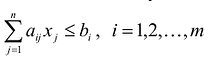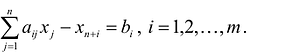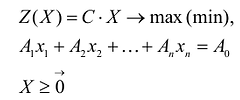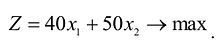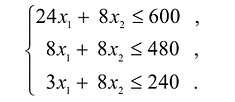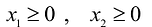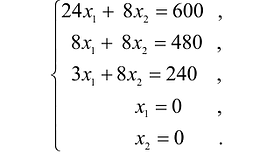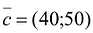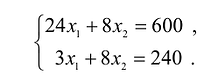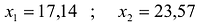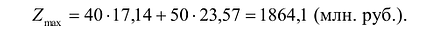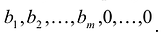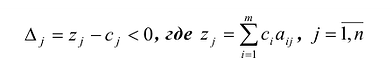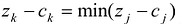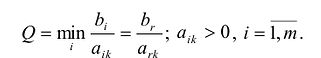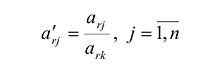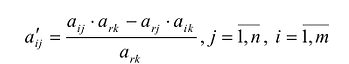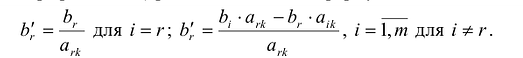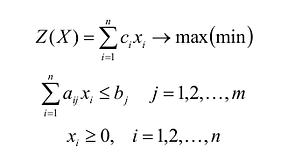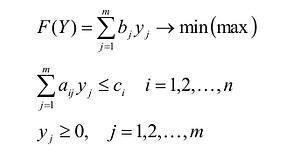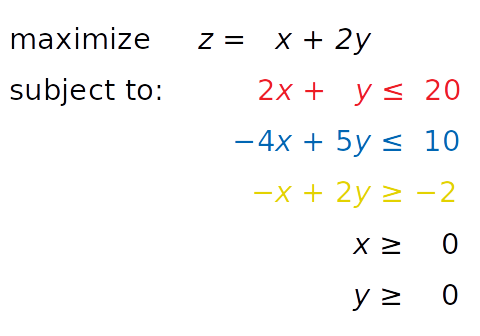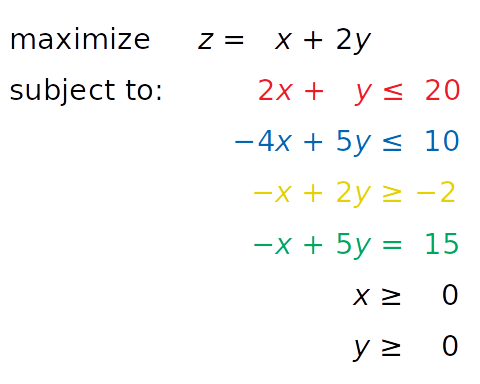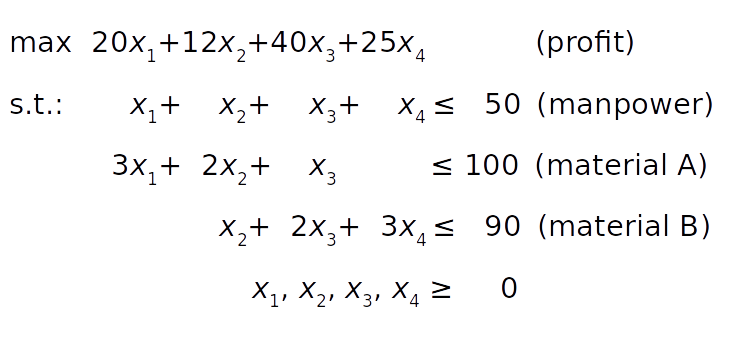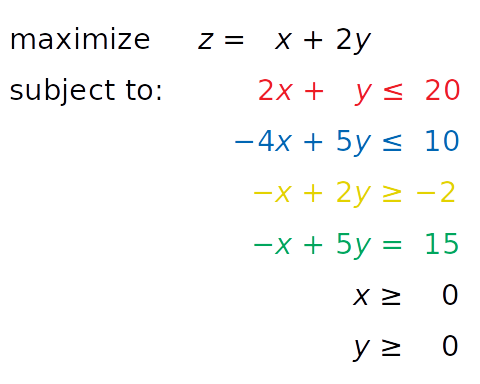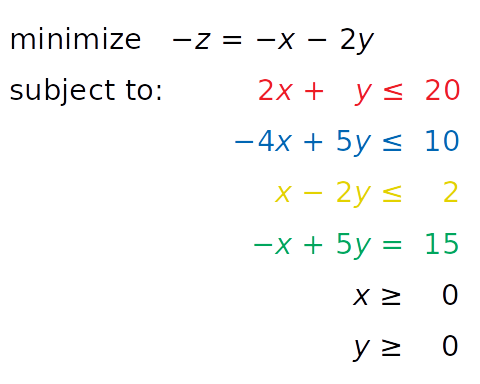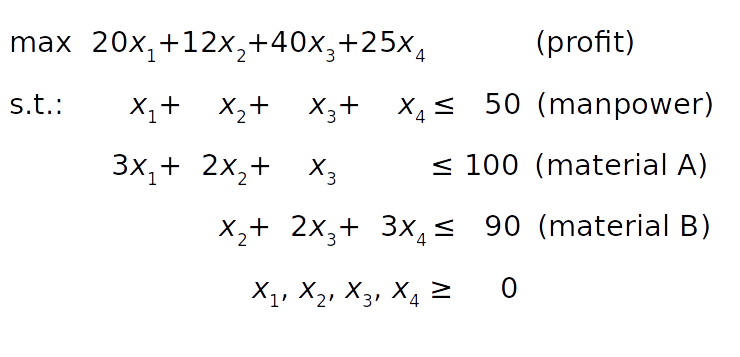Решение системы уравнений линейного программирования

Решение задач линейного программирования

Решение происходит в три этапа:

Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
Решение симплексным методом;

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min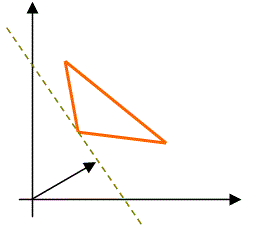

F(x) → max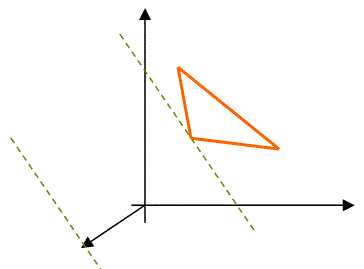

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m₊₁,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Линейное программирование — основные понятия с примерами решения

Содержание:

Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.

Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.

Построение математической модели экономической задачи включает следующие этапы:

выбор переменных задачи;
составление системы ограничений;
выбор целевой функции.

Переменными задачи называются величины

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 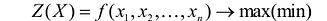и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:

Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:

Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (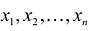). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любойX = (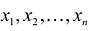). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

Используя знак суммирования эту задачу можно записать следующим образом:

Каноническая задача линейного программирования в векторной форме имеет вид:

В данном случае введены векторы:

Здесь С — X — скалярное произведение векторов С и X.

Каноническая задача линейного программирования в матричной форме записи имеет вид:

Здесь А — матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 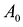— матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

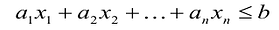
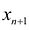
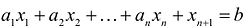
прибавляется величина такая, что переводит неравенство в равенство , где:

Неотрицательная переменная называется дополнительной переменной.

Основания для возможности такого преобразования дает следующая теорема.

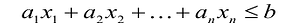
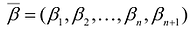
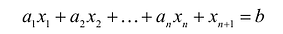
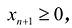
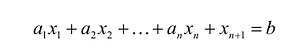
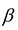
Теорема. Каждому решению неравенства соответствует единственное решение уравнения: и неравенства и, наоборот, каждому решению уравнения: и неравенства соответствует единственное решение неравенства:

Доказательство. Пусть — решение неравенства. Тогда:

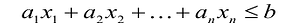
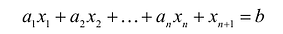
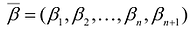
Если в уравнение вместо переменных подставить значения , получится:

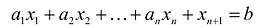
Таким образом, решение удовлетворяет уравнению: и неравенству .

Доказана первая часть теоремы.

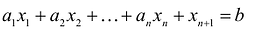
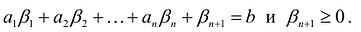
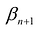
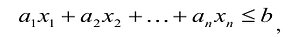
Пусть удовлетворяет уравнению и неравенству , т.е. . Отбрасывая в левой части равенства неотрицательную величину , получим:

т.е. удовлетворяет неравенству: что и требовалось доказать.

Если в левую часть неравенств системы ограничений вида

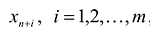
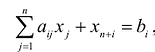
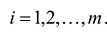
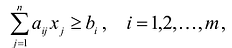
добавить переменную , то получится система ограничений — уравнений В случае, если система неравенств-ограничений имеет вид , то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную

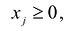
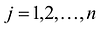
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

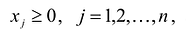
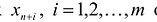
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах , а правые части — наличие производственных ресурсов, то числовые значения дополнительных неизвестных и означают объем неиспользованных ресурсов i-го вида.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Множества допустимых решений

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.

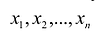
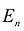
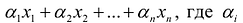
Выпуклой линейной комбинацией произвольных точек Евклидова пространства называется сумма — произвольные неотрицательные числа, сумма которых равна 1.

Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.

Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.

Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.

Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.

Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.

Так, угловые точки треугольника — его вершины, круга — точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.

Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.

Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.

Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.

Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.

Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.

Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.

Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.

Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками

Каноническая задача линейного программирования в векторной форме имеет вид:

Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.

Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 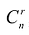, где n — число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.

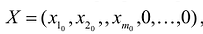
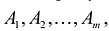
Опорным решением задачи линейного программирования называется такое допустимое решение , для которого векторы условий, соответствующие положительным координатам линейно независимы.

Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).

Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теорема. Любое опорное решение является угловой точкой области допустимых решений.

Теорема. Любая угловая точка области допустимых решений является опорным решением.

Пример:

Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.

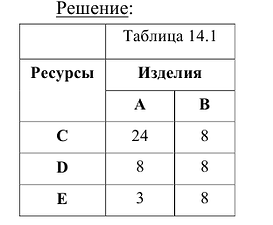
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1

Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В — 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.

Построим математическую модель задачи, для чего обозначим 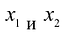— объемы производства изделий А и В соответственно.

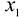
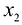
Тогда прибыль предприятия от реализации изделий А и изделий В составит:

Ограничения по ресурсам будут иметь вид:

Естественно, объемы производства должны быть неотрицательными

Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:

Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

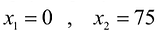
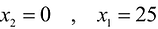
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: а при .

Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой

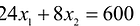
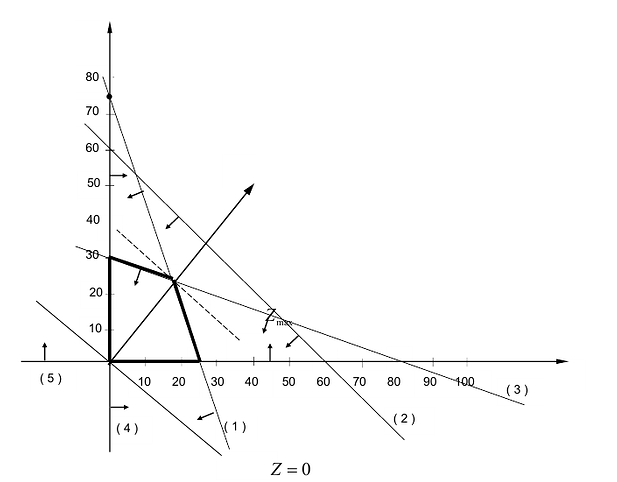
. На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 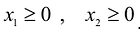, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.

Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции

имеет координаты

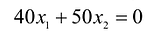
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.

Решив эту систему, получаем, что

Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:

Алгоритм решения задачи линейного программирования графическим методом таков:

Строится область допустимых решений;
Строится вектор нормали к линии уровня с точкой приложении в начале координат;
Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.

В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.

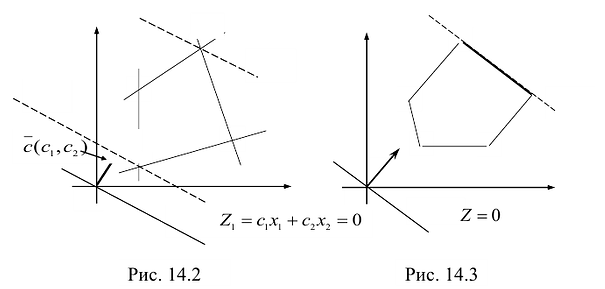
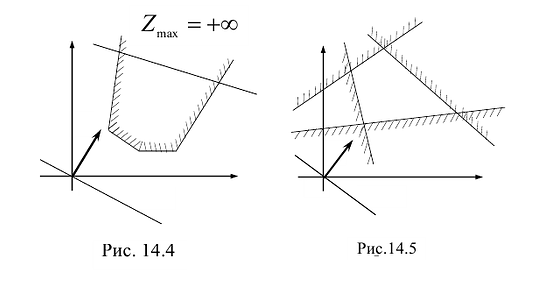
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.

Основные понятия симплексного метода решения задачи линейного программирования.

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.

Симплекс-метод основан на следующих свойствах задачи линейного программирования:

Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
Множество всех планов задачи линейного программирования выпукло.
Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.

Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).

Симплекс-метод с естественным базисом

Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:

Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

Теорема 2. Если для всех векторов выполняется условие 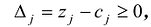то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 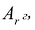, который дает минимальное положительное отношение:

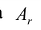
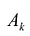
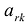
Строка называется направляющей, столбец и элемент — направляющими (последний называют также разрешающим элементом).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

а элементы любой другой i-й строки пересчитываются по формулам:

Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.

Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.

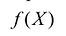
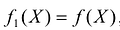
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы следует искать максимум функции затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.

Симплексный метод с искусственным базисом (М-метод)

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М — достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Теория двойственности

Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.

Любую задачу линейного программирования можно записать в виде:

Первоначальная задача называется исходной или прямой.

Модель двойственной задачи имеет вид:

Переменные двойственной задачи 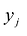называют объективно обусловленными оценками или двойственными оценками.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🐍 Линейное программирование. Практика решения задач оптимизации на Python

Leo Matyushkin

Данная публикация представляет собой сокращенный перевод руководства Мирко Стожилковича Hands-On Linear Programming: Optimization With Python. Для удобства читателей текст перевода также адаптирован в виде Jupyter-блокнота.

Линейное программирование – это набор методов, используемых в математическом программировании, также называемых математической оптимизацией. Эти методы используются для решения систем линейных уравнений и неравенств, перед которыми стоит цель максимизации или минимизации некоторой линейной функции. Линейное программирование используется в научных вычислениях, экономике, технических науках, производстве, транспорте, военном деле, логистике, энергетике и т. д.

Экосистема Python включает несколько мощных инструментов линейного программирования. Из этого руководства вы узнаете:

что такое линейное программирование и в чем его польза;
какие инструменты Python подходят для линейного программирования;
как построить модель и решить задачу линейного программирования на Python.

Что собой представляет линейное программирование

Системы линейных уравнений и неравенств часто имеют множество возможных решений.

Линейное программирование – это набор математических и вычислительных инструментов, позволяющих найти конкретное решение системы, которое соответствует максимуму или минимуму какой-либо другой линейной функции. Линейное программирование – это фундаментальный метод оптимизации, десятилетиями применяемый в областях, требующих большого объема математических вычислений. Эти методы точны, сравнительно быстры и подходят длямножества практических приложений.

Смешанно-целочисленное линейное программирование – это вид линейного программирования, которое фокусируется на обработке задач, где хотя бы одна переменная принимает дискретные целые, а не непрерывно меняющиеся значения.

Целочисленные переменные важны для правильного представления количеств, естественным образом выражаемых целыми числами, таких как число выпущенных самолетов или количество обслуженных клиентов.

Особенно важным видом целочисленных переменных являются бинарные переменные, имеющие лишь значения 0 или 1 , и полезные при принятии решений вида «да»/«нет». Например, следует ли строить завод, включить или выключить машину. Также их можно использовать для имитации логических ограничений.

Смешанно-целочисленное линейное программирование позволяет преодолеть многие ограничения линейного программирования. Можно аппроксимировать нелинейные функции кусочно-линейными, использовать полунепрерывные переменные, логические ограничения модели. Это требовательный к ресурсам инструмент, но достижения в области компьютерного оборудования и программного обеспечения сделали его более доступным.

Линейное программирование на Python

Базовый метод решения задач линейного программирования называется симплекс-методом, другой популярный подход – метод внутренней точки. Задачи смешанного целочисленного линейного программирования решаются с помощью более сложных и ресурсоемких методов, таких как метод ветвей и границ.

Заметим, что почти все широко используемые библиотеки линейного программирования и смешанно-целочисленного линейного программирования написаны на языках Fortran, C или C++, так как линейное программирование требует интенсивной вычислительной работы с матрицами, часто очень большими. Соответствующие инструменты Python – это просто удобные интерфейсы для работы с низкоуровневыми библиотеками – солверами.

В этом руководстве для определения и решения задач линейного программирования мы будем использовать Python-библиотеки SciPy и PuLP.

1. Примеры задач линейного программирования

1.1. Небольшой показательный пример

Рассмотрим следующую задачу максимизации:

Нам нужно найти такие x и y , чтобы выполнялись «красное», «синее» и «желтое» неравенства, а также ограничения x ≥ 0 и y ≥ 0 . При этом решение должно соответствовать максимально возможному значению z .

Независимые переменные, которые нужно найти ( x и y ) называют переменными решения (decision variables). Функция, которую необходимо максимизировать или минимизировать ( z ), – это целевая функция (objective function), функция стоимости (cost function) или просто цель (goal). Неравенства (или уравнения), которым необходимо удовлетворять, называются ограничениями (inequality constraints или equality constraints для обычных уравнений).

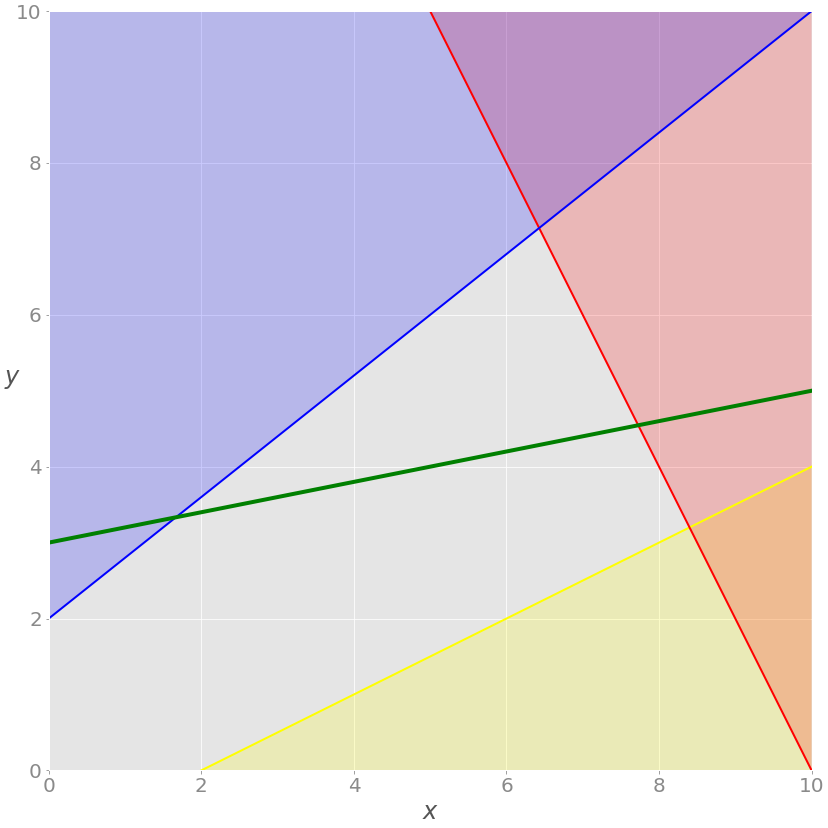
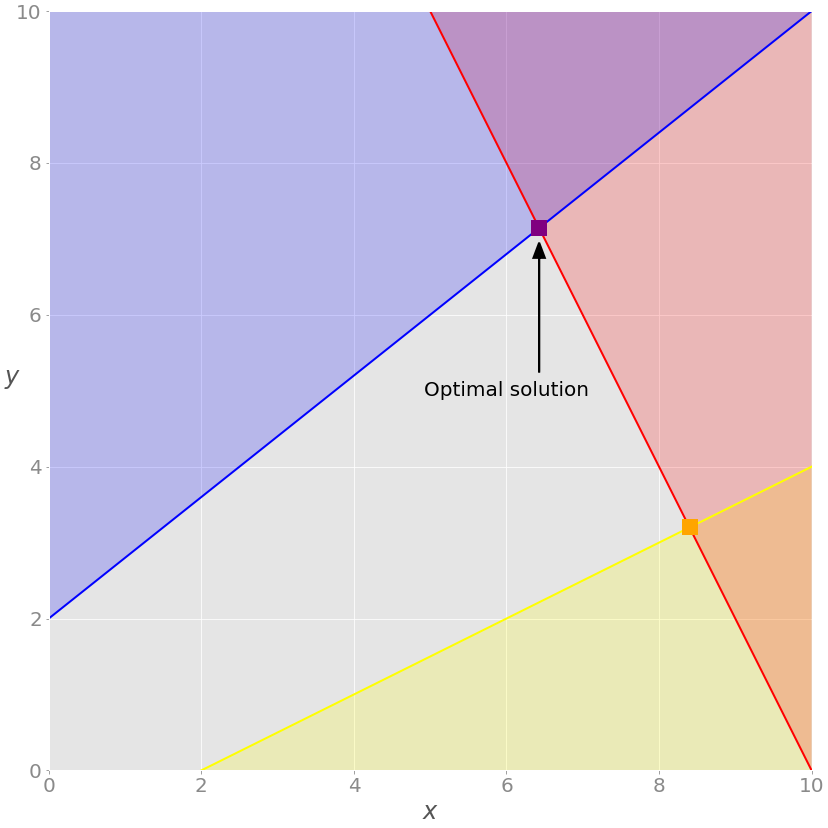
Проблему можно визуализировать следующим образом.

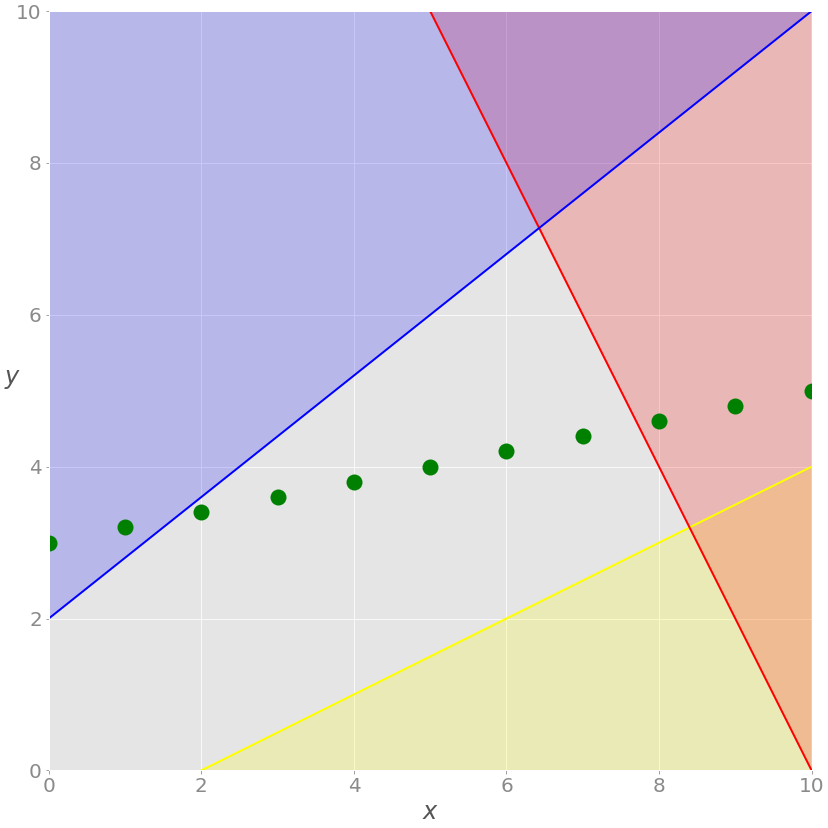
2x + y = 20 , а красная область над ней показывает, где красное неравенство не выполняется. Аналогично синяя линия – это −4x + 5y = 10 , желтая линия – это −x + 2y = −2 , окрашенные области – та часть плоскости, где неравенство не выполняется.» data-src=»https://media.proglib.io/posts/2020/11/26/5a6c3e3ee24ae5a228d7a0ee4ea9fb8a.png» > Красная линия представляет функцию 2x + y = 20 , а красная область над ней показывает, где красное неравенство не выполняется. Аналогично синяя линия – это −4x + 5y = 10 , желтая линия – это −x + 2y = −2 , окрашенные области – та часть плоскости, где неравенство не выполняется.

Каждая точка серой области удовлетворяет всем ограничениям и является потенциальным решением задачи. Эта область называется областью допустимых решений (feasible region), а ее точки – допустимыми решениями (feasible solutions).

Мы хотим максимизировать z . Решение, соответствующее максимальному значению z , называют оптимальным решением.

Обратите внимание, что функция z линейна. Оптимальное решение должно находиться в одной из вершин области допустимых решений. Иногда весь край допустимой области или даже вся область может соответствовать одному и тому же значению z .

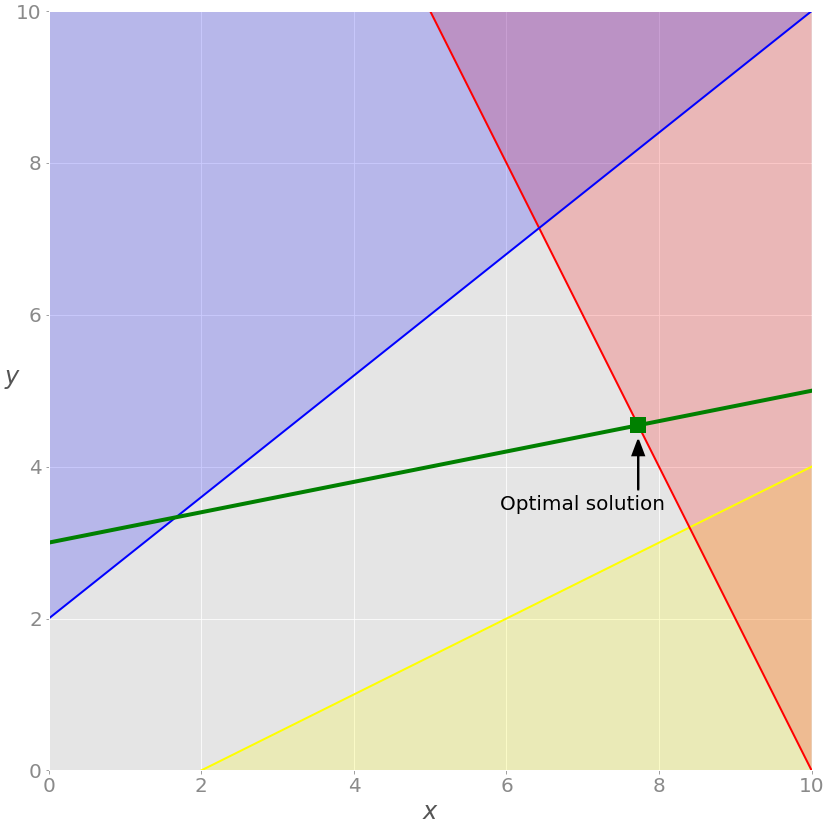
Представим, что в задачу введено дополнительное ограничение в виде равенства, окрашенного зеленым:

Его можно визуализировать, добавив соответствующую зеленую прямую:

Теперь область допустимых решений не соответствует всей серой зоне. Это лишь часть зеленой линии, проходящей через серую область от точки пересечения с синей линией до точки пересечения с красной.

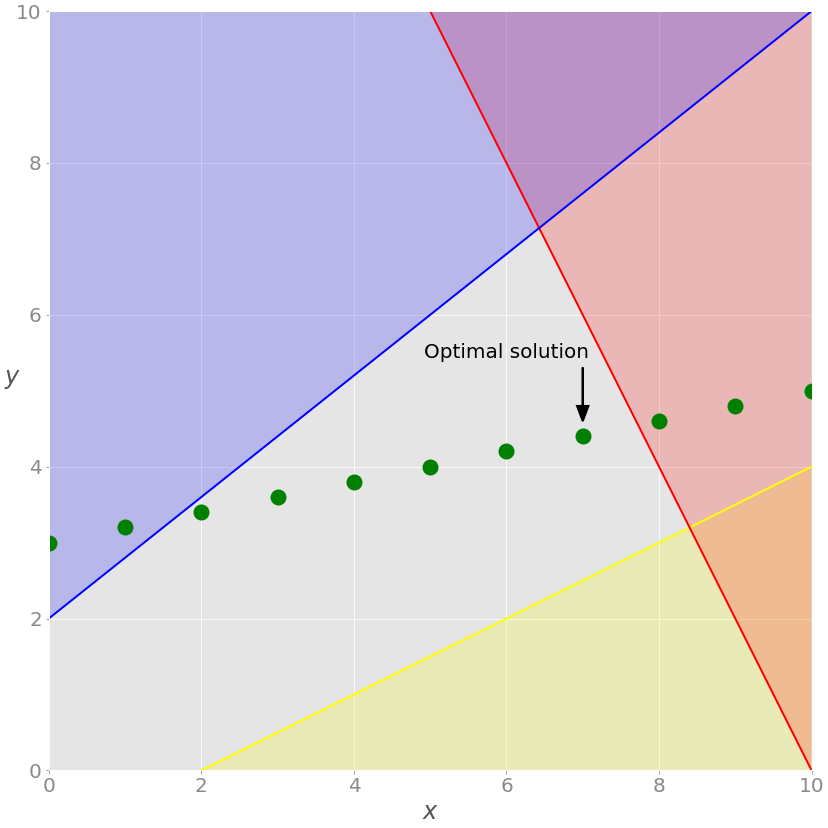
Если добавить требование, что все значения x должны быть целыми числами, то мы получим задачу смешанно-целочисленного линейного программирования, и набор возможных решений снова изменится:

Больше нет зеленой линии – только дискретные точки, где значение x является целым числом. Возможные решения – это зеленые точки на сером фоне.

Эти три примера иллюстрируют задачи линейного программирования – они имеют ограниченные допустимые области решений и конечные решения.

Когда ни одно решение не может удовлетворить все ограничения сразу, задача в рамках линейного программирования неразрешима.

1.2. Задача о распределении ресурсов

В предыдущих разделах мы рассмотрели абстрактную задачу линейного программирования, не связанную с каким-либо реальным приложением. В этом разделе речь пойдет о более практической задачи оптимизации, связанной с распределением ресурсов на производстве.

Предположим, что фабрика производит четыре различных продукта, ежедневное количество первого продукта составляет x_1 , второго продукта – x_2 и т. д. Цель – определить максимальную прибыль ежедневного объема производства для каждого продукта с учетом следующих условий:

Прибыль (profit) на единицу продукта составляет 20, 12, 40 и 25 долларов для каждого из четырех продуктов соответственно.
Из-за нехватки рабочей силы (manpower) общее количество единиц, производимых в день, не может превышать 50.
На каждую единицу 1-го продукта расходуется 3 единицы сырья A. Каждая единица 2-го продукта требует 2 единиц сырья A и 1 единицы сырья B. Каждой единице 3-го продукта требуется 1 единица A и 2 единицы B. Наконец, каждая единица 4-го продукта требует трех единиц. B.
Из-за ограничений по транспортировке и хранению фабрика может потреблять до 100 единиц сырья A и 90 единиц B в день.

Математическую модель можно определить так:

Целевая функция (прибыль) определяется в условии 1. Ограничение рабочей силы следует из условия 2. Ограничения на сырье A и B могут быть получены из условий 3 и 4 путем суммирования потребностей в сырье для каждого продукта. Наконец, количество продуктов не может быть отрицательным.

В отличие от предыдущего примера, эту задачу не так удобно визуализировать, потому как она имеет четыре переменных. Однако принципы остаются теми же.

2. Линейное программирование на Python. Практическая реализация

В этом руководстве мы будем использовать для решения описанной выше задачи линейного программирования два пакета Python :

SciPy – универсальный пакет для научных вычислений с Python. Его внутренний пакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.
PuLP – API линейного программирования Python для определения задачи и вызова солверов. По умолчанию в качестве солвера используется COIN-OR Branch and Cut Solver (CBC). Еще один отличный солвер с открытым исходным кодом – GNU Linear Programming Kit (GLPK).

2.1. Установка SciPy и PuLP

Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP.

Возможно, вам потребуется запустить pulptest или sudo pulptest , чтобы включить солверы PuLP, особенно если вы используете Linux или Mac:

2.2. Использование SciPy

В этом разделе мы рассмотрим, как использовать библиотеку SciPy по оптимизации и поиску корней для линейного программирования. Начнём с импорта scipy.optimize.linprog() :

2.3. Решение первого примера c помощью SciPy

Начнём с решения первого (дополненного) примера:

linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений-неравенств со знаком больше или равно ( ≥ ). Чтобы обойти эти проблемы, нам необходимо изменить описание задачи перед запуском оптимизации:

Вместо максимизации z = x + 2y минимизируем отрицательное значение ( −z = −x − 2y ).
Вместо знака ≥ мы можем умножить «желтое» неравенство на -1 и получить противоположный знак (ограничения по осям рассмотрим далее).

На следующем шаге определяем входные значения:

Мы поместили значения из системы в соответствующие списки:

obj содержит коэффициенты целевой функции,
lhs_ineq и rhs_ineq содержат коэффициенты из ограничений-неравенств,
lhs_eq и rhs_eq содержат коэффициенты из ограничивающего уравнения.

Следующим шагом является определение границ каждой переменной. В данном случае они находятся между нулем и положительной бесконечностью:

Однако эти границы совпадают с установленными по умолчанию в linprog() .

Наконец, пришло время оптимизировать и решить интересующую нас проблему:

Параметр c относится к коэффициентам из целевой функции. A_ub и b_ub соответственно связаны с коэффициентами из левой и правой частей ограничений-неравенств. Точно так же A_eq и b_eq относятся к ограничениям уравнений. Параметр bounds служит для указания нижней и верхней границ переменных решения.

Параметр method определяет используемый алгоритм линейного программирования. Доступны три варианта:

по умолчанию используется метод внутренней точки: method = «inner-point»,
измененный двухфазный симплекс-метод method=»revised simplex»,
симплекс-метод method=»simplex»

linprog() возвращает структуру данных со следующими атрибутами:

.con – остатки ограничения-равенства;
.fun – оптимальное значение целевой функции (если найдено);
.message – словесный статус решения;
.nit – количество итераций, необходимых для завершения расчета;
.slack – значения так называемых дополнительных переменных – разниц между значениями левой и правой сторонами ограничений;
.status – целое число от 0 до 4, отражающих результат решения: например, 0, когда было найдено оптимальное решение;
.success – логическое значение, показывающее, найдено ли оптимальное решение;
.x – массив NumPy, содержащий оптимальные значения переменных решения.

Доступ к атрибутам можно получить по отдельности:

Графически результат можно отобразить следующим образом.

Вначале наша задача органичивалась только неравенствами. Если удалить параметры зеленого уравнения A_eq и b_eq из вызова linprog() , получим следующий результат:

2.4. Решение задачи о производстве с помощью SciPy

Рассмотрим теперь решение второй задачи – о продуктах, рабочей силе и используемом сырье.

Как и в предыдущем примере, нам нужно извлечь необходимые векторы и матрицу из задачи, передать их в качестве аргументов в linprog() :

Максимальная прибыль составляет 1900 и соответствует x_1 = 5 и x_3 = 45 . В данных условиях производить второй и четвертый продукты невыгодно. Результат позволяет сделать несколько интересных выводов:

Третий продукт приносит наибольшую прибыль.
Первая дополнительная переменная ( slack ) равна 0. Это означает, что равны значения левой и правой сторон ограничения для рабочей силы. Завод производит 50 единиц в день, и это его полная мощность.
Вторая дополнительная переменная равна 40: фабрика потребляет 60 единиц сырья A (15 единиц для первого продукта и 45 для третьего) из возможных 100 единиц.
Третья дополнительная переменная равен 0: фабрика потребляет все 90 единиц сырья B. При этом все это количество потребляется для производства третьего продукта. Вот почему фабрика вообще не может производить второй или четвертый товар и не может произвести более 45 единиц третьего товара. Cырья B просто не хватает.

Возможности линейного программирования SciPy полезны в основном для небольших задач. Для более крупных и сложных проблем разумно использовать другие библиотеки:

SciPy не поддерживает работу с целочисленными переменными решения.
SciPy не подразумевает запуск внешних солверов.
SciPy не предоставляет классы или функции для построения моделей. Определять массивы и матрицы вручную для крупных задач слишком утомительно.
Также вручную приходится переопределять задачи, как мы это сделали выше.

2.5. Решение первой задачи на линейное программирование с помощью PuLP

Итак, PuLP имеет более удобный API линейного программирования, чем SciPy. Начнем с импорта.

Первый шаг – инициализировать экземпляр LpProblem для описания модели:

Параметр sense определяет, решаем ли мы задачу минимизации (параметр LpMinimize или 1 , установлен по умолчанию) или максимизации ( LpMaximize или -1 ).

Создав модель, мы можем определить переменные решения как экземпляры класса LpVariable :

Значения границ по умолчанию – отрицательная и положительная бесконечности, поэтому в нашем случае необходимо указать нижнюю границу ( lowBound = 0 ).

Необязательный параметр cat определяет категорию переменной решения. При работе с непрерывными переменными можно использовать значение по умолчанию «Continuous» .

Переменные x и y теперь можно использовать для создания других PuLP-объектов, представляющих линейные выражения и ограничения:

Построив линейную комбинацию нескольких переменных решения, мы получаем экземпляр pulp.LpAffineExpression , представляющий линейное выражение. Выражения можно комбинировать с операторами == , и >= и получать экземпляры pulp.LpConstraint – линейные ограничения вашей модели.

Опишем теперь ограничения. В отличие от SciPy, с PuLP не нужно создавать списки и матрицы. Просто записываем выражения Python и добавляем в модель с помощью оператора += :

LpProblem позволяет добавлять ограничения в модель, определяя их как кортежи. Первый элемент кортежа – экземпляр LpConstraint , второй – его удобочитаемое имя.

Аналогично описывается целевая функция:

Теперь можно посмотреть полное определение модели:

Строковое представление модели содержит все соответствующие данные: цель, переменные, ограничения и их имена.

Теперь мы готовы решить задачу. Достаточно лишь вызвать метод .solve() для объекта модели.

Метод .solve() вызывает базовый солвер, изменяет объект модели и возвращает целочисленный статус решения, равный 1, если найден оптимум. Остальные коды состояний описаны в документации.

Результаты оптимизации доступны в виде атрибутов модели:

model.objective содержит значение целевой функции, model.constraints – значения дополнительных переменных, а объекты x и y имеют оптимальные значения переменных решения.

Результаты получились примерно такие же, как у SciPy.

Чтобы получить смешанно-целочисленное решение, достаточно обозначить это при помощи параметра cat :

Теперь x – целое число, как указано в модели. Этот факт меняет решение. Покажем это на графике:

Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне. Это решение с наибольшими значениями как x , так и y , дающее максимальное значение целевой функции.

2.6. Решение задачи о производстве с помощью PuLP

Подход к определению и решению второй задачи такой же, как и в предыдущем примере:

Как видите, решение согласуется с тем, что мы молучили с помощью SciPy. Наиболее выгодное решение – производить в день 5 единиц первого продукта и 45 единиц третьего.

Давайте сделаем задачу более интересной. Допустим, из-за проблем с оборудованием, фабрика не может производить первую и третью продукцию параллельно. Какое решение наиболее выгодно в этом случае?

Теперь у нас есть еще одно логическое ограничение: если x_1 положительно, то x_3 должно равняться нулю, и наоборот. Здесь пригодятся бинарные переменные решения. Введем две переменные y_1 и y_3 , которые будут обозначать, генерируются ли вообще первый или третий продукты:

При таких условиях оказывается, что оптимальный подход – исключить первый продукт вовсе и производить только третий.

Заключение

Теперь вы в общих чертах представляете, с какими задачами имеет дело линейное программирование и как использовать Python для решения подобных задач.

Теперь – после прохождения этого руководства – вы умеете:

определить модель, которая описывает задачу в SciPy и PuLP;
создать программу Python для оптимизационной задачи;
запустить программу оптимизации, чтобы найти решение задачи;
получить результат оптимизации.

Если вы хотите узнать больше о линейном программировании, вот несколько отправных точек, с которых можно начать:

Следите за нашими тегами Python и Математика!

источники:

http://www.evkova.org/linejnoe-programmirovanie

http://proglib.io/p/lineynoe-programmirovanie-praktika-resheniya-zadach-optimizacii-na-python-2020-11-26