Решение системы уравнений максвелла волновое уравнение

Уравнения Максвелла и волновое уравнение

Электромагнитные волны

В процессе распространения механической волны в упругой среде в колебательное движение вовлекаются частицы среды. Причиной этого процесса является наличие взаимодействия между молекулами.

Помимо упругих волн в природе существует волновой процесс иной природы. Речь идет об электромагнитных волнах, представляющих собой процесс распространения колебаний электромагнитного поля. По существу мы живем в мире ЭМВ. Их диапазон невероятно широк – это радиоволны, инфракрасное излучение, ультрафиолетовое, рентгеновское излучения, γ – лучи. Особое место в этом многообразии занимает видимая часть диапазона – свет. Именно с помощью этих волн мы получаем подавляющее количество информации об окружающем мире.

Что такое электромагнитная волна? Какова ее природа, механизм распространения, свойства? Существуют ли общие закономерности, характерные как для упругих, так и для электромагнитных волн?

Уравнения Максвелла и волновое уравнение

Электромагнитные волны интересны тем, что первоначально они были «открыты» Максвеллом на бумаге. Основываясь на предложенной им системе уравнений, Максвелл показал, что электрическое и магнитное поля могут существовать в отсутствие зарядов и токов, распространяясь в виде волны со скоростью 3∙10 8 м/с. Спустя почти 40 лет предсказанный Максвеллом материальный объект – ЭМВ – был обнаружен Герцем экспериментально.

Уравнения Максвелла являются постулатами электродинамики, сформулированными на основе анализа опытных фактов. Уравнения устанавливают связь между зарядами, токами и полями – электрическим и магнитным. Обратимся к двум уравнениям.

1. Циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру l пропорциональна скорости изменения магнитного потока через поверхность, натянутую на контур (это закон электромагнитной индукции Фарадея):

(1)

Физический смысл этого уравнения – меняющееся магнитное поле порождает электрическое поле .

2. Циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру l пропорциональна скорости изменения потока вектора электрической индукции через поверхность, натянутую на контур:

(2)

Физический смысл этого уравнения – магнитное поле порождаетcя токами и меняющимся электрическим полем .

Даже без каких-либо математических преобразований этих уравнений понятно: если в какой-то точке меняется электрическое поле, то в соответствии с (2) возникает магнитное поле. Это магнитное поле, изменяясь, порождает в соответствие с (1) электрическое поле. Поля взаимно индуцируют друг друга, они уже не связаны с зарядами и токами!

Более того, процесс взаимного индуцирования полей будет распространяться в пространстве с конечной скоростью, то есть возникает электромагнитная волна. Для того, чтобы доказать факт существования в системе волнового процесса, в котором колеблется величина S, необходимо получить волновое уравнение

Рассмотрим однородный диэлектрик с диэлектрической проницаемостью ε и магнитной проницаемостью μ. Пусть в этой среде существуют магнитное поле . Для простоты будем полагать, что вектор напряженности магнитного поля располагается вдоль оси ОY и зависит только от координаты z и времени t: .

Записываем уравнения (1) и (2) с учетом связи между характеристиками полей в однородной изотропной среде: и :

Найдем поток вектора через прямоугольную площадку KLMN и циркуляцию вектора по прямоугольному контуру KLPQ ( KL = dz, LP= KQ = b, LM = KN = a)

Очевидно, что поток вектора через площадку KLMN и циркуляция по контуру KLPQ отличны от нуля. Тогда циркуляция вектора по контуру KLMN и поток вектора через поверхность KLPQ тоже отличны от нуля. Такое возможно только при условии, что при изменении магнитного поля возникло электрическое поле , направленное вдоль оси ОX.

Вывод 1: При изменении магнитного поля возникает электрическое поле, напряженность которого перпендикулярна индукции магнитного поля .

С учетом сказанного система уравнений перепишется

После преобразований получаем:

Продифференцируем первое уравнение (1.1) по координате z, второе уравнение (2.1) – по времени t:

Электрическое поле, порождаемое меняющимся магнитным полем, подчиняется волновому уравнению! Это означает, что возникшее электрическое поле подчиняется законам распространения волн.

Нетрудно видеть, что если продифференцировать первое уравнение (1.1) по времени t, второе уравнение (2.1) — по координате z , получим уравнение

Магнитное поле тоже подчиняется волновому уравнению, причем волна бежит в том же направлении, что и волна .

Дата добавления: 2018-09-25 ; просмотров: 3433 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

2.6. Электромагнитные волны

Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды () и токи (j = 0):

Величины и — электрическая и магнитная постоянные, соответственно, которые связаны со скоростью света в вакууме соотношением

Постоянные и характеризуют электрические и магнитные свойства среды, которую мы будем считать однородной и изотропной.

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.

Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.

Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.

При строго гармоническом изменении во времени векторов и электромагнитная волна называется монохроматической.

Получим из уравнений Максвелла волновые уравнения для векторов и .

Волновое уравнение для электромагнитных волн

Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.

Возьмем ротор от обеих частей уравнения

При этом воспользуемся доказываемой в курсе математики формулой:

где — введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:

Получаем в итоге:

Выразим rotB через электрическое поле с помощью уравнения Максвелла:

и используем это выражение в правой части (2.93). В результате приходим к уравнению:

и вводя показатель преломления среды

запишем уравнение для вектора напряженности электрического поля в виде:

Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:

Взяв ротор от обеих частей уравнения Максвелла

и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:

Полученные волновые уравнения для и означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна

В отсутствие среды (при ) скорость электромагнитных волн совпадает со скоростью света в вакууме.

Основные свойства электромагнитных волн

Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:

Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:

Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:

Дифференцирование плоских волн по времени дает:

Тогда из уравнений Максвелла следует:

Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:

Далее, ни у , ни у нет компонент параллельных оси х:

Иными словами и в изотропной среде,

электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.

Тогда можно выбрать координатные оси так, чтобы вектор был направлен вдоль оси у (рис. 2.27):

Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне

В этом случае уравнения (2.103) приобретают вид:

Отсюда следует, что вектор направлен вдоль оси z:

Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:

Отсюда вытекает обычная связь волнового вектора, частоты и скорости:

а также связь амплитуд колебаний полей:

Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.

Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.

Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).

На рис. 2.28 представлена шкала электромагнитных волн.

Рис. 2.28. Шкала электромагнитных волн

Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.

Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.

http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.

http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».

http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.

http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.

Эффект Доплера для электромагнитных волн

Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:

Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:

Подставим эти выражения в выражение для фазы , чтобы получить фазу волны в движущейся системе отсчета:

Это выражение можно записать как

где и — циклическая частота и волновой вектор относительно движущейся системы отсчета. Сравнивая с (2.110), находим преобразования Лоренца для частоты и волнового вектора:

Для электромагнитной волны в вакууме

Пусть направление распространения волны составляет в первой системе отсчета угол с осью х:

Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:

Это и есть формула Доплера для электромагнитных волн.

Если , то наблюдатель удаляется от источника излучения и воспринимаемая им частота волны уменьшается:

Если , то наблюдатель приближается к источнику и частота излучения для него увеличивается:

При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E₀ вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H₀ и вектора магнитной индукции B₀ в волне.

Ответ находим сразу из уравнений (3.127), где полагаем :

Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:

Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время площадка получила от волны энергию . Тогда переданный площадке импульс равен

На площадку действует со стороны волны сила

Давление Р, оказываемое волной, равно

Если средняя плотность энергии в волне равна , то на площадь А за время попадет энергия из объема и

Отсюда находим давление электромагнитной волны (света):

Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.

Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:

Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.

Решение уравнений Максвелла; потенциалы и волновое уравнение

Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.

Начнем с V·В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В — есть ротор чего-то. Поэтому, если вы записали

то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А′, если A′=A+ vψ), где ψ — любое скалярное поле, потому что ротор vψ — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)

Теперь разберем закон Фарадея VxE= –∂B/∂t, потому что он не содержит никаких токов или зарядов. Если мы запишем В как V X А и продифференцируем по t, то сможем переписать закон Фарадея в форме

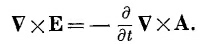Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде

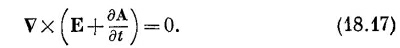Мы видим, что E+∂A/∂t — это вектор, ротор которого ранен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было VxE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от –φ (минус для технических удобств). То же самое сделаем и для E+∂A/∂t; мы полагаем

Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂A/∂t исчезает, Е будет нашим старым –vφ. Итак, закон Фарадея можно представить в форме

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.

Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим А на A′=A+vψ? В общем, Е должно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и φ вместе по правилам

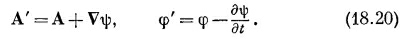Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.

Раньше мы выбирали V ·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники ρ и j. Раз мы можем определить А и φ из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в v·E=ρ/ε₀; получаем

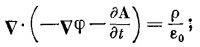это можно записать еще в виде

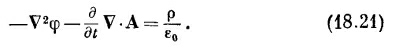Таково первое уравнение, связывающее φ и А с источниками.

Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

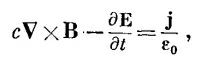а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

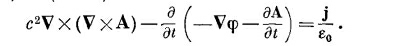Первый член можно переписать, используя алгебраическое тождество v x (vxA) = V (V·A) – v 2 A; мы получаем

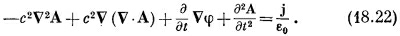Не очень-то оно простое!

К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для φ разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая ,

Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

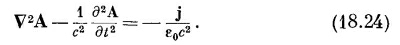И наше уравнение (18.21) для φ принимает такую же форму:

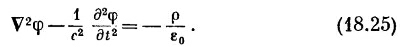Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂t) 2 , когда мы раскроем ее, то обнаружим

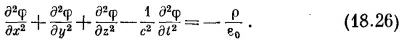Это уравнение имеет приятную симметрию по х, у, z, t; здесь (–1/с 2 ) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.

Уравнения Максвелла привели нас к нового типа уравнению для потенциалов φ и А, но с одной и той же математической формой для всех четырех функций φ, А_х, А_у и A_z. Раз мы научились решать эти уравнения, то можем получить В и Е из vXE и —vφ —∂A/∂t. Мы приходим к другой форме электромагнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.
Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме

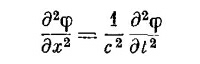и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что φ и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность φ и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.

С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и φ в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные уравнения в терминах E и В. Но они — по ту сторону горы, на которую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе — нас ожидают новые, прекрасные пейзажи.