Решение системы уравнений методом крамера matlab
% Решим систему методом Крамера
A = [1 2 3 4; -1 2 -3 4; 0 1 -1 1; 1 1 1 1];
b = [30;10;3;10];
% Проверим невырожденность системы
rank(A)
% По правилу Крамера
A1 = A;
A2 = A;
A3 = A;
A4 = A;
A1(:,1) = b;
A2(:,2) = b;
A3(:,3) = b;
A4(:,4) = b;
x1 = det(A1) / det(A);
x2 = det(A2) / det(A);
x3 = det(A3) / det(A);
x4 = det(A4) / det(A);
x=[x1;x2;x3;x4];
Решение СЛАУ и матрицы в Matlab
Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.
Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.
В традициях нашего сайта разберём на примере:
Решить систему линейных уравнений:
4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4
Метод обратной матрицы в Matlab
Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.
В итоге у нас получится 2 матрицы:
Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:
После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:
Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.
Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.
Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.
Метод Гаусса
Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:
Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.
Метод разложения матрицы
Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.
Возможны следующие разложения:
- разложение Холецкого
- LU разложение
- QR разложение
Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.
Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.
LU разложение
Решим выше предложенную задачу через LU разложение:
QR разложение
И через QR разложение соответственно:
Отметим, что апостроф ( ‘ ) после Q означает транспонирование.
Стандартные функции Matlab
Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:
Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.
Повторение
Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:
Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1
- Методом обратной матрицы:
- Методом Гаусса:
- LU разложение:
- QR разложение:
На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.
Методы решения систем линейных алгебраических уравнений
Расчет установившихся режимов электрических систем
1.схема замещения электрической сети не содержит замкнутых контуров
Индивидуальное задание
Для схемы, представленной на рис.1 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки заданы в таблице 1.
Рис. 1
 |  |  |  |
| А | А | А | |
| 5+j6 |  |  |
Данный раздел должен содержать:
· краткие теоретические сведения,
· обобщенное уравнение состояния,
· вычисление обратной матрицы для матрицы 
· вычисление обратной матрицы для матрицы 
· вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы,
1.краткие теоретические сведения
2.обобщенное уравнение состояния

Уравнение (1) объединяет два матричных уравнения.
Уравнение по первому закону Кирхгофа
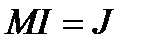
Уравнение по второму закону Кирхгофа

3.вычисление обратной матрицы для матрицы 
1) Записываем матрицу 
2) Заменяем каждый элемент матрицы 
3) Этот определитель сопровождаем знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.
4)Делим полученную матрицу на 
вычислением определитель классическим методом
4. вычисление обратной матрицы для матрицы 
5. вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы
1) аналитическим методом
2)с помощью MATLAB- программы
2.схема замещения электрической сети содержит замкнутые контуры
Индивидуальное задание
Для схемы представленной на рис.2 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. 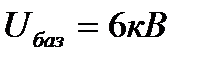
Рис. 2
 |  |  | 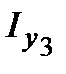 |  |  |  |  |
| А | А | А | Ом | Ом | Ом | Ом | |
| 50 | 100 | 100 | 1 | 2 | 3 | 2 |
Данный раздел должен содержать:
· краткие теоретические сведения,
· первую и вторую матрицы инциденций,
· обобщенное уравнение состояния,
· решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса),
· решение матричного уравнения состояния методом Крамера в системе MATLAB,
· сравнение полученных промежуточных результатов, найденных разными способами,
· вычисление узловых напряжений аналитически,
· нахождение узловых напряжений с помощью MATLAB- программы,
· сравнение полученных результатов, найденных разными способами.
1.краткие теоретические сведения
2. первая и вторая матрица инциденций
Первая матрица инциденций без балансирующего узла будет иметь вид:

В нашей схеме замещения всего один независимый контур, в соответствии с этим вторая матрица инциденций примет вид:

3.обобщенное уравнение состояния

4.решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса)
1) метод обратной матрицы
Находим решение с помощьюMATLAB

Тогда запишем систему уравнений




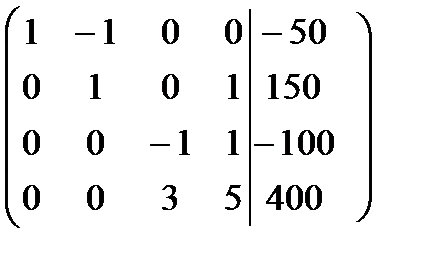


На главной диагонали, преобразованной матрицы коэффициентов, стоят 1. Теперь проведем преобразования в соответствии с обратным ходом метода Гаусса.
Из последнего уравнения системы определяем 

В результате получаем вектор-столбец искомых неизвестных
5.решение матричного уравнения состояния методом Крамера в системе MATLAB
http://codetown.ru/matlab/slau-matricy/
http://megapredmet.ru/2-4697.html