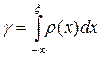Решение системы уравнений методом монте карло

VMath

Инструменты сайта

Основное

Информация

Действия

Вспомогательная страница к разделу СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Для понимания материалов этого пункта полезно ознакомиться с идеологией метода Монте-Карло

Решение системы линейных уравнений методом Монте-Карло

Рассмотрим систему из $ n_<> $ линейных уравнений относительно $ n_<> $ неизвестных $$ \left\< \begin a_<11>x_1 &+a_<12>x_2&+ \ldots&+a_<1n>x_n &=b_1,\\ a_<21>x_1 &+a_<22>x_2&+ \ldots&+a_<2n>x_n &=b_2,\\ \dots & & & & \dots \\ a_x_1 &+a_x_2&+ \ldots&+a_x_n &=b_n, \end \right. $$ которую иногда будем представлять и в матричном виде $$ AX= \mathcal B \ . $$ Решение этой системы равносильно нахождению минимума квадратичной функции $$ F(X)=\sum_^n \alpha_j \left(a_x_1+\dots+a_x_n-b_j \right)^2= (AX-\mathcal B)^ <\top>\left( \begin \alpha_1 & 0 & \dots & 0 \\ 0 & \alpha_2 & \dots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \dots & \alpha_n \end \right) (AX-\mathcal B) \ , $$ где $ \< \alpha_j\>_^n $ — положительные числа, а $ <>^ <\top>$ означает транспонирование.

Если исходная система линейных уравнений имеет единственное решение $ X=X_<\ast>=(x_<1\ast>,\dots, x_) $, то в пространстве $ \mathbb R^ $ уравнение $$ F(X) = 1 $$ задает эллипсоид с центром в точке $ X_ <\ast>$. Каждая из $ (n_<>-1) $-мерных гиперплоскостей $ x_k=x_ $ ( линейных многообразий), проходящих через центр эллипсоида, делит его объем пополам.

Построим $ n_<> $-мерный параллелепипед $$ A_1 ☞ ЗДЕСЬ: $$ V_ <\mathrm E>\approx 3133.207748 \ . $$ $$ \begin N & 1000 & 5000 & 10000 & 20000 & 50000 \\ \hline M & 62 & 297 & 581 & 1181 & 2885 \\ \hline V_ <\Pi>M/N & 3339.6300 & 3199.581 & 3129.5565 & 3180.7282 & 3108.0105 \\ \hline \overline <\xi_1>& 3.2592 & 3.2745 & 3.1230 & 3.1020 & 3.1798 \\ \hline \overline <\xi_2>& 0.9406 & 1.5346 & 1.4669 & 1.4867 & 1.5141 \\ \hline \overline <\xi_3>& 0.3453 & 0.5163 & 0.3996 & 0.5001 & 0.4299 \\ \hline \overline <\xi_4>& -1.7029 & -2.2198 & -2.1676 & -2.1545 & -2.2413\\ \end $$ Решение системы $$ x_1=\frac<257> <84>\approx 3.05952,\ x_2=\frac<53> <36>\approx 1.47222,\ x_3=\frac<55> <126>\approx 0.43651 , x_4=-\frac<547> <252>\approx -2.17063 \ . $$

Источник

Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний Монте-Карло и его реализация в цифровых машинах. М.: Физматгиз, 1961. 266 с.

Алгоритм Монте-Карло для решения систем линейных алгебраических уравнений методом Зейделя∗ Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Товстик Татьяна Михайловна, Волосенко Ксения Сергеевна

Для решения системы линейных алгебраических уравнений методом Монте-Карло используется алгоритм последовательных приближений. Очередная итерация моделируется в виде случайного вектора, математическое ожидание которого совпадает с приближением процесса итерации в форме Зейделя. Выводится система линейных уравнений, которым удовлетворяют взаимные корреляции компонент предельного вектора и корреляции двух последовательных приближений. Доказывается существование и конечность предельных дисперсий случайного вектора решений системы. Библиогр. 7 назв. Табл. 1.

MONTE CARLO ALGORITHM FOR SOLUTION OF A SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS BY THE SEIDEL’S METHOD

For solution of a system of linear algebraic equations by the Monte Carlo method a method of the successive approximations is used. The next in turn iteration is modeled as a random vector, the expectation of which coincides with the corresponding Seidel’s iteration. The existence and the boundedness of dispersions of the limiting vector is proved. The system of linear equations, to which satisfy the cross-correlations of the limiting vector, and the limiting correlations of two successive approximations is delivered. All these correlations are unknowns of the common linear system and may be found only simultaneously. The boundedness of dispersions of the limiting vector leads to the stochastic stability of algorithm. The number of iterations giving the desirable exactness is estimated. As an examples, the systems of the orders of n = 3 and n = 100 are studied. Refs 7. Tables 1.

Текст научной работы на тему «Алгоритм Монте-Карло для решения систем линейных алгебраических уравнений методом Зейделя∗»

Вестник СПбГУ. Сер. 1. Т. 3(61). 2016. Вып. 3

ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ*

Т. М. Товстик, К. С. Волосенко

Санкт-Петербургский государственный университет,

Российская Федерация, 199034, Санкт-Петербург, Университетская наб., 7—9

Ключевые слова: алгоритм Монте-Карло, метод Зейделя, система линейных алгебраических уравнений.

1. Введение. Метод Монте-Карло для решения системы линейных алгебраических уравнений рекомендуется использовать в том случае, если ее порядок достаточно велик [1]. В монографиях [1, 2] с помощью метода Монте-Карло вычисляется одна компонента вектора решения или скалярное произведение вектора решения и произвольного вектора. В работах 3 оценивается сразу весь вектор решений. В работе [3] используется стохастический метод итераций, причем математическое ожидание случайного вектора очередной итерации совпадает с суммой соответствующего отрезка ряда Неймана. В статьях [4, 5] представлены алгоритмы Монте-Карло, позволяющие получать итерационное решение системы линейных уравнений при условиях более слабых, чем условия обычного метода Монте-Карло. В данной работе, в отличие от алгоритма в [3], особенность построения случайного вектора заключается в том, что математическое ожидание очередной итерации совпадает с итерацией Зейделя [6]. В дополнение к работе [7] доказывается существование и конечность предельных дисперсий случайного вектора решений системы.

Пусть задана система линейных алгебраических уравнений вида

где А = — квадратная матрица, а X = (Хь . Хп)т и / = (/ь . fn)T —

В работе рассматривается алгоритм Монте-Карло, в основе которого лежит метод Зейделя. Будем предполагать, что для нормы матрицы A выполняется условие

IIAll = max ]Т\Aik| 1.

2. Алгоритм Монте-Карло для метода Зейделя. Рассмотрим метод, который имитирует алгоритм Зейделя. Будем моделировать случайные векторы то > 0 такие, что выполняется £(0) = /, а при то > 1 справедливо Е £(т) = X(т), причем компоненты X(т) удовлетворяют равенствам (3). В основе моделирования лежит имитация цепи Маркова, которая задается вектором начального распределения п и стохастической матрицей Р вероятностей перехода:

\\Pij||, Р. > ° 1 0 для тех пар (г,]), для которых справедливо Аг. = 0. На матрицу Р не накладывается никаких ограничений. В частности, она может состоять из отдельных блоков.

Моделирование вектора С(т) осуществляется следующим способом. Выбирается начальное приближение С(0) = /, далее при то > 1 компоненты случайного вектора обновляются последовательно, начиная с г = 1, причем при моделировании г-й компоненты учитывается результат обновления всех предыдущих компонент ((т\ ] 1 моделируются последовательно, начиная от г = 1 до п по формулам

(т) , 1 ^АЪ /РЪ пРи ^ г,

где случайные состояния ^ разыгрываются в соответствии с распределением (5). Формулы (6) допускают представление

Лг) Ai,ji Am) i Ai,j Am— 1) , x 1 г»

Q =2^X(k,ji)-j2-Cji ‘+2^X(k,ji)-j2-Cji > + fi, г = 1,2. п, (7)

где X(k,p) — символ Кронекера.

Вычисление математического ожидания от обеих частей равенства (7) приводит к равенствам

ЕСГ = £ Aij EZ(m) + ^ ECjm—1) + fi, г = 1, 2. n, m > 1. (8) j=1 j=i

Отсюда при m =1 получаем

EZ(1) = £ A1j fj + f1, EZ(1) = £ Aij Ej + E Aij fj + fi, г = 2. n. (9)

Из формул (9) следуют равенства EZ(1) = X(1), EZ(1) = X(1), в которых X(1) те же, что и в (3) метода Зейделя, если начальный вектор удовлетворяет X(0) = f. Нетрудно проверить, что при всех m > 1 выполнены равенства EZ(m) = X\m\ Теорема 1. Пусть для системы линейных алгебраических уравнений вида

k=1 Piji k=i Piji

Тогда справедливы равенства

ECr = ХГ = £ AijX(m) + ^ Aijx(m—1) + fi, 1 0 при то ^ ж для всех г. Так как имеет место равенство Е(г(т) = Х(т), выполняется \Хг — Е^™^ —> 0 при то ^ ж, тем самым теорема доказана.

Для оценки решения уравнения (1) следует достаточно большое число N

раз моделировать случайный вектор С(М), тогда будем иметь ес(м) « Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Теорема 2. Пусть выполнены условия теоремы 1 и норма матрицы В = [В. ] = [А. /ргз] удовлетворяет неравенству

\\В\\ = та? £Вш 1. Пользуясь равенствами (6), находим второй момент разности

/ Ат) с \ тл I ^(т)\ Лг(т)

(С /г) и с учетом Е I Сг ) = Х> получаем

2 г — 1 Л2 2 п л2 2

Е (с(т)) =Е—Е(Сзт)) +Е—Е(^1)) то > 1. (18)

Равенство (18) дает

КГ] — КТ—1) = £ Вгз (Ц) — К.— 1)) + £ Вгз — 1) — Я.^ +

+ 2fi (X(m) — X(m-1)) . (19)

Покажем, что для всех г будет выполняться \Я(т) — Я™ ^^ 0 при то ^ ж.

В [6] доказано, что в методе Зейделя для разностей итераций X(т), X(т—1) справедливы неравенства

||Х(т) _х(т-1)|| М 0 такие, что выполняется ат Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Пользуясь равенствами (23) и симметрией ковариаций Д™1^, получаем неравенства, аналогичные (20),

Пример 1. Рассмотрим систему линейных алгебраических уравнений вида (1), где матрица А и вектор f определяются выражениями

0.3 —0.5 0.1 A = I —0.2 0.3 0.4 0.4 -0.3 0.2

Норма матрицы А равна ||А|| = ш&х^ | = 0.9. Элементы матрицы Р вычис-

лялись по формулам

1 М*, а при больших N N = 106 и больше), наоборот, брать М Надоели баннеры? Вы всегда можете отключить рекламу.

Решение линейных алгебраических систем методом Монте-Карло

Существует множество методов решения линейных алгебраических систем методом статистических испытаний[2]. Рассмотрим метод применимый к решению системы линейных алгебраических уравнений общего вида

, (9)

Решение системы (9) равносильно минимизации квадратичной формы:

, (10)

Учитывая (10), определим n-мерный эллипсоид

. (11)

Пусть — вектор решения системы уравнений (9), тогда очевидно, что вектор является центром симметрии эллипсоида (11). Это означает, что каждая из гиперплоскостей , проходящая через центр эллипсоида, делит его объем пополам. По этой причине решение системы (9) сводится к нахождению таких значений , что объемы частей эллипсоида, лежащих в полупространствах и совпадают и равняются половине объема эллипсоида (11).

Из данных соображений вытекает следующий способ решения. Возьмем n-мерный параллелепипед

в который заведомо помещается n-мерный эллипсоид.

Рассмотрим статистическую серию из N векторов

, (12)

где k = 1,2,…,N и случайная компонента равномерно распределена на отрезке [A_i,B_i], i = 1,…,n.

Отберем среди набора векторов (12) те, которые попадают в эллипсоид (11), т.е. удовлетворяют условию . Пусть таких векторов оказалось M. Рассмотрим среднее арифметическое векторов, попавших в эллипсоид, тогда можно записать следующее представление:

, (13)

из которого следует способ нахождения вектора решений исходной системы уравнений (9).

Можно оценить дисперсию случайной величины (13). Она равна

где V¢ — n-мерный объем, удовлетворяющий неравенству .

На листинге_№6 приведен код программы, которая решает систему уравнений (9) методом Монте-Карло согласно алгоритму (13).

%Задача решения линейной алгебраической системы

%уравнений ax=b методом Монте-Карло

%Определяем размерность системы уравнений (9)

%Определяем вектор решений x0 системы уравнений (9)

%В качестве матрицы a выбираем случайную матрицу,

%а правую часть b находим из уравнения b=ax0

%Определяем параллелепипед, в который помещается

%Оцениваем константу С, входящую в определение

%Организуем цикл расчетов с разными длинами

%статистических серий N

%решения x к точному решению x0

%Рисуем зависимость относительной ошибки от длины

%статистической серии N

%Определяем квадратичную форму (10)

На рис.6 приведен итог работы кода программы листинга_№6. На фигуре изображена кривая, изображающая динамику относительной ошибки error = ||x — x₀||/||x₀||, где x — численное решение системы уравнений (9), а x₀ — точное решение системы уравнений (9).

Рис.6. Решение линейной системы уравнений (9) методом
Монте-Карло

Вычисление интегралов

Значение случайной функции f(x) заключено между f(x) и f(x + dx), если случайная величина x заключена между x и x + dx. Вероятность такого события равна r(x)dx. В этом случае математическое ожидание и дисперсия случайной функции можно оценить согласно формулам:

, (14)

. (15)

Первый способ вычисления интегралов с помощью метода Монте-Карло базируется на формуле (14), т.е. одномерный интеграл можно рассматривать как математическое ожидание случайной функции f(x), аргумент которой является случайной величиной с плотностью распределения r(x).

Математическое ожидание можно приближенно вычислить, исходя из центральной предельной теоремы теории вероятностей. Если h является случайной величиной, то среднее арифметическое N испытаний

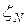
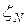
также является случайной величиной с тем же математическим ожиданием, т.е. , при это распределение случайной величины стремится к нормальному распределению с дисперсией при N ® ¥. Таким образом, при большом числе испытаний дисперсия будет малой величиной, а значение средней арифметической с вероятностью близкой к единице будет близко к математическому ожиданию. Учитывая эти соображения, можно положить

, (16)

где x — случайная величина с плотностью распределения r(x).

Оценим дисперсию (15), заменяя в ней математические ожидания на соответствующие суммы типа (16), тогда

. (17)

Делитель N — 1 вместо N в (17) связан с тем соображением, что для оценки выборочной дисперсии используется так называемая несмещенная оценка. Впрочем, это существенно лишь при малой длине выборки N.

При статистических испытаниях численные оценки тех или иных величин носят вероятностный характер, т.е. они в принципе могут как угодно сильно отличаться от точного значения. Однако, согласно свойствам нормального распределения, с вероятностью 99,7% ошибка не превосходит три стандартных отклонения, т.е. величины . При увеличении числа статистических испытаний N ошибка ответа будет уменьшаться, примерно, как . Отметим, что зависимость относится не к самой ошибке, а к тем доверительным интервалам, в которые ошибка попадает с заданной вероятностью.

В качестве примера найдем методом статистических испытаний интеграл

, (18)

значение которого равно нулю. Применим к интегралу формулы (15), (16), тогда получим следующие расчетные формулы

, (19)

, (20)

где x — случайная величина с плотностью , — выборочная дисперсия. Случайную величину x для решения задачи (18) — (20) разыграем согласно формуле (7), где g — равномерно распределенная на отрезке [0,1] случайная величина, генерируемая с помощью генератора псевдослучайных чисел (5) с параметрами A = 5 13 и g₀ = 2 — 36 .

На листинге_№7 приведен код программы взятия интеграла (18) методом Монте-Карло по формулам (19), (20).

%Пример взятия интеграла (18) методом статистических

%испытаний согласно формулам (19), (20)

%Задаем число удвоений числа статистических испытаний

%Задаем значения констант A и gamma0 для генерации

%согласно алгоритму (5) псевдослучайных чисел,

%распределенных равномерно на отрезке [0,1]

%Организуем цикл расчетов с различным числом

%статистических испытаний N

%Генерируем последовательность псевдослучайных

%чисел gamma, согласно алгоритму (5), а также

%случайные числа xi с плотностью 0.5*exp(-abs(x))

gamma=gamma0; I(n)=0; s=0;

%Вычисляем искомый интеграл I и соответствующую

%дисперсию delta согласно формулам (19), (20)

%Вычисляем доверительный интервал con_int с

%Определяем массив с числом испытаний в каждом

%Рисуем сходимость численного значения интеграла (18)

%в зависимости от числа испытаний N в отдельном

%Рисуем зависимость длины доверительного интервала с

%99,7% надежностью от числа испытаний N в отдельном

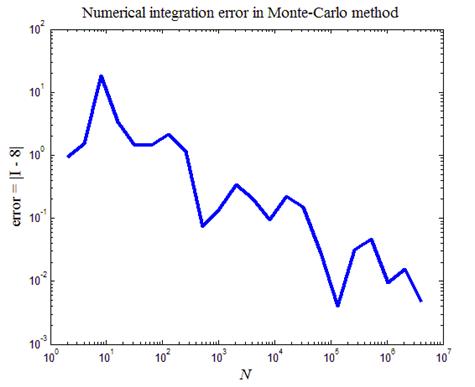
На рис.7 приведен итог работы кода программы листинга_№7. На левом рисунке приведена зависимость абсолютного значения искомого интеграла от числа испытаний в статистическом эксперименте (все координаты выбраны логарифмическими). Видна сходимость в среднем численной оценки к искомому значению интеграла, равному нулю. На правом рисунке приведена зависимость границы доверительного интервала с надежностью 99,7% от числа испытаний в статистическом эксперименте. Согласно определению доверительного интервала, введенному в выборочном методе статистики, искомое значение интеграла I с вероятностью » 99,7% находится в интервале

Рис.7. Численное взятие интеграла (18) методом Монте-Карло

Второй метод взятия интеграла методом статистических испытаний применяется к интегралам вида , при этом считается, что 0 £ f(x) £ 1, x Î [0,1]. Произвольный интеграл можно привести к такому виду некоторой линейной заменой переменных.

Пусть имеется набор из N пар <(g₁,g₂),(g₃,g₄),…,(g₂_N_—₁,g₂_N)>, равномерно распределенных на единичном отрезке случайных чисел. Рассмотрим пары чисел как координаты точек единичного квадрата координатной плоскости x и y (левый график на рис.8).

Поскольку точки на плоскости распределены случайно и равномерно в единичном квадрате, постольку вероятность попадания точки под кривую y = f(x) равна площади, заключенной под кривой, т.е. искомому интегралу I = . Условие попадания точки под кривую определяется неравенством . Доля точек из всего набора N точек, которая удовлетворяет данному неравенству, дает приближенное значение искомого интеграла.

Рис.8. Взятие интеграла 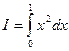методом статистических испытаний

На листинге_№8 приведен код программы численного взятия интеграла методом статистических испытаний.

%Пример взятия интеграла от функции y=x^2 вторым

%способом в методе статистических испытаний

%Создаем массив точек на плоскости (x,y) со

%случайными, равномерно распределенными на

%единичном отрезке числами

%Определяем подынтегральную функции yi=xi^2

%Рисуем массив случайных точек и

%Определяем число удвоений числа точек на

%плоскости, координаты которых равномерно

%распределены на единичном отрезке

%Организуем цикл расчетов искомого интеграла

%для различного количества случайных точек на

if y(i) 2 , а также N = 1000 случайных точек в единичном квадрате. Подсчитывалась доля точек, которые оказывались ниже кривой y = x 2 . На правом рисунке изображена зависимость ошибки численного интегрирования error = |I — 1/3| от параметра N — числа точек в статистической серии. Видно, что в среднем, по мере роста параметра N, ошибка численного интегрирования стремится к нулю.

Оптимизация дисперсии. Точность взятия интеграла методом Монте-Карло можно повысить, подбирая специальным образом случайную величину. Пусть g(x) = f(x)r(x), тогда исходный интеграл запишется в виде: , где функция r(x) нормирована таким образом, что ее можно считать плотностью распределения некоторой случайной величины. Задача состоит в том, чтобы, путем подбора плотности распределения r(x), добиться минимума дисперсии (15).

В дисперсии отдельного испытания (15) второе слагаемое , оно не зависит от плотности r(x), поэтому условие минимума сводится к условию:

Добавляя условие нормировки плотности r(x), получим следующую задачу оптимизации:

Находя вариационные производные и приравнивая их нулю, получим

Для равенства вариационных производных нулю необходимо и достаточно, чтобы , т.е. . В этом случае дисперсия не просто минимальна, а равна нулю, когда g(x) знакопостоянна.

На практике взять не удается, т.к. для моделирования случайной величины с такой плотностью необходимо решить уравнение

которое равносильно по сложности исходной задаче взятия интеграла I. По этой причине плотность r(x) подбирают так, чтобы уравнение

относительно x решалось просто, а сама плотность r(x) была как можно ближе к g(x).

Смысл увеличения точности состоит в том, что, если r(x)

|g(x)|, то f(x) почти постоянна и все испытания дают близкие результаты.

В качестве примера рассмотрим взятие интеграла

» 0.13940279264033. (21)

Будем считать, что 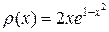, при этом . Случайную величину с такой плотностью разыгрываем согласно формуле

Откуда следует, что

, (22)

. (23)

На листинге_№9 приведен код программы взятия интеграла (21) с помощью алгоритма статистических испытаний с уменьшенной дисперсией, т.е. с помощью вычислительных формул (22), (23).

%Взятие интеграла (21) методом Монте-Карло

%с уменьшенной дисперсией по формулам (22), (23)

%Определяем число удвоений количества чисел

%в статистической серии

%Организуем цикл расчетов с различными

%длинами статистических серий

%Определяем искомый интеграл (21) согласно

%вычислительной формуле (23)

%Определяем дисперсию численной оценки

%Определяем ошибку численной оценки

%Определяем границу доверительного интервала

%с надежностью 99,7%

%Рисуем зависимость ошибки численной оценки

%интеграла от количества испытаний N в

%Рисуем зависимость границы 99,7% надежности от

%количества испытаний N в статистической серии

На рис.9 приведен итог работы кода программы листинга_№9. На левом рисунке приведена зависимость ошибки численного интегрирования от длины статистической серии. По сравнению с предыдущим примером точность заметно повысилась. На правом рисунке приведена зависимость границы доверительного интервала с 99,7% надежностью от длины статистической серии. Этот график заметно отличается от аналогичного графика, представленного на рис.7. При одной и той же длине статистической серии N границы доверительного интервала значительно уже в данном случае, чем в том примере, который приведен на рис.7 и где процедура оптимизации дисперсии не проводилась.

Рис.9. Взятие интеграла (20) методом статистических испытаний с
уменьшенной дисперсией

Многомерные интегралы. Второй способ легко обобщается на многомерные интегралы по единичному кубу G, если значения подынтегральной функции лежат в единичном интервале.

Рассмотрим для определенности трехмерное пространство с координатами x, y, z и интеграл вида

. (24)

Интеграл (24) легко берется путем его факторизации и взятием трех одномерных интегралов.

Пусть определена совокупность N четверок (g₁,g₂,g₃,g₄), (g₅,g₆,g₇,g₈), …, (g₄_N_—₃,g₄_N_—₂,g₄_N_—₁,g₄_N), равномерно распределенных на единичном интервале случайных чисел. Каждая из четверток определяет случайную точку в единичном четырехмерном кубе . Доля случайных точек, удовлетворяющих неравенству , где определяет приближенное значение искомого интеграла.

На листинге_№10 приведен код программы взятия интеграла (24) вторым способом в методе статистических испытаний.

%Численное интегрирование вторым способом в

%методе статистических испытаний на примере

%взятия многомерного интеграла (24)

%Определяем число удвоений количества точек N

%в статистической серии

%Вычисляем искомый многомерный интеграл

x=rand; y=rand; z=rand; u=rand;

if u 22 » 4,2×10 6 точность лучше 10 — 4 .

Рассмотренный выше второй способ вычисления кратных интегралов менее точен, чем первый способ. Рассмотрим более подробно процедуру использования первого способа при подсчете кратных интегралов методом статистических испытаний. Обозначим через r(x,y,z) ³ 0 многомерную плотность распределения некоторой случайной величины, тогда по аналогии с одномерным случаем, имеем

. (25)

Взятие интеграла согласно способу (25) сводится к разыгрыванию многомерной случайной величины. Для разыгрывания первой переменной x построим одномерную плотность распределения по этой переменной при произвольных остальных

Функция R(x) неотрицательна и нормирована на единицу, т.е. является плотностью некоторой случайной величины, поэтому можно записать следующую формулу разыгрывания:

где g₃_i _—₂ — случайная величина, равномерно распределенная на единичном отрезке.

Найдем плотность распределения по второй координате y при фиксированной первой и произвольной третьей. Как нетрудно проверить, искомая плотность имеет вид:

В этом случае разыгрывание второй координаты сводится к решению уравнения

Плотность распределения по третьей координате z при фиксированных первых двух имеет вид:

Откуда следует последняя формула разыгрывания

В качестве примера вычисления интеграла вторым способом рассмотрим интеграл вида:

. (26)

В качестве многомерной плотности распределения возьмем функцию 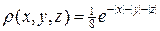. Функции r соответствуют одномерные плотности распределения вида:

(27)

С учетом (27) расчетная формула для вычисления интеграла (26) запишется в виде:

. (28)

На листинге_№11 приведен код программы численного взятия интеграла (26) с помощью первого способа в методе статистических испытаний. С учетом вида случайных величин (27), расчетная формула для искомого интеграла приведена в (28).

%Программа расчета многомерного интеграла

%(26) с помощью первого способа в методе

%статистических испытаний по расчетной

%Определяем количество удвоений числа точек

%N в серии статистических испытаний

%Определяем случайные величины xi, eta и dz,

%используемые в расчетной формуле (28)

gmxi=rand; gmeta=rand; gmdz=rand;

%Определяем искомый интеграл

%Оцениваем ошибку численного расчета

%Рисуем зависимость ошибки численного

%интегрирования от количества случайных

%точек N в статистической серии

Рис.11. Зависимость ошибки численного интегрирования при взятии
интеграла (26) от числа точек N в статистической серии

На рис.11 приведен итог работы кода программы листинга_№11. Построена кривая, описывающая зависимость ошибки численного интегрирования методом статистических испытаний от длины N статистической серии. Видно, что в среднем точность растет по мере роста числа точек в статистической серии.

Обсудим вопрос о соотношении сеточных и статистических методов численного интегрирования. Пусть функция m переменных интегрируется с помощью некоторого сеточного метода p-го порядка точности. Будем считать, что сетка по каждой из переменных имеет n узлов. В этом случае полное число узлов есть N = n m , а погрешность расчета e

n — p . Исключая n из последних двух соотношений, находим число узлов необходимое для достижения заданной точности . При использовании одного из методов статистических испытаний погрешность , т.е. число случайных точек в статистической серии .

Из сравнения двух формул и следует, что при m 2p более предпочтительными являются статистические методы. Последнее неравенство указывает на то, что для численного взятия многомерных интегралов предпочтительными являются методы статистических испытаний.

Пусть, например, подынтегральная функция имеет непрерывные вторые производные, тогда можно рассчитывать на второй порядок точности, т.е. p = 2. В этом случае трехмерные интегралы, согласно вышеупомянутым неравенствам, выгодно интегрировать сеточными методами, а пятимерные — статистическими.

Решение краевых задач

Решение краевых задач методом Монте-Карло рассмотрим на примере задачи Дирихле для уравнения Лапласа[3].

Пусть G — односвязная область, на границе которой ¶G задана функция f = f(Q), Q Î ¶G. Требуется найти такую функцию u(P), которая внутри области G удовлетворяет уравнению Лапласа:

. (29)

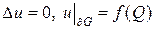
Построим в области G квадратную сетку с шагом h. Узлы данной сетки делятся на два типа: регулярные и нерегулярные (Лекция №9). Каждый регулярный узел имеет четыре соседних узла P₁, P₂, P₃, P₄ из области G согласно шаблону, приведенному на рис.7,б из лекции №9. Нерегулярный или граничный узел не имеет ровно четырех соседей из области G.

Составим разностную схему для уравнения Лапласа (29) на квадратной сетке и перепишем полученное уравнение следующим образом:

. (30)

Для решения конечно-разностной задачи (30) составим следующую теоретико-вероятностную схему. Будем считать, что величина пропорциональна плотности неких частиц в узле P. Каждая частица может с вероятностью ¼ за одни шаг по времени перейти в один из четырех соседних узлов: P₁, P₂, P₃, P₄. Таким образом, частицы, первоначально находящиеся в некотором узле, за один шаг по времени уходят из него, а другие частицы из соседних узлов могут прийти в исходный узел. Считаем, что частица, приходящая на границу области, поглощается.

Вероятность u(P,Q) того, что частица, выйдя из регулярного узла P, окончит блуждание в граничном узле Q, удовлетворяет условию (30), т.е.

(31)

и краевому условию

(32)

Если промоделировать блуждание частицы по решетке N раз, заставляя каждый раз ее выходить из точки P и подсчитывать количество L ее приходов в точку Q, то отношение является приближенным решением задачи (31) с краевыми условиями (32).

Перейдем к решению задачи Дирихле в общем случае. Пусть, когда частица оказывается в точке Q, с нее берется штраф f(Q). Величина штрафа принимает значения f(Q₁),…,f(Q_s), где Q₁,…,Q_s — совокупность всех граничных узлов. Согласно (31), (32), вероятность заплатить штраф f(Q_j) равна u(P,Q_j). Среднее значение штрафа w(P), которое заплатит произвольная частица, выходящая из регулярной точки P, определяется по формуле:

. (33)

Покажем, что выражение (33) удовлетворяет уравнению

Действительно, подставим в (31) вместо Q — Q_j и умножим обе части на f(Q_j), тогда, после суммирования по j, получим уравнение (33). Для граничных узлов функция w(P) удовлетворяет краевым условиям. Так, после подстановки P = Q в (33) согласно (32) пропадут все слагаемые, кроме одного, т.е.

т.е. w(P) удовлетворяет конечно-разностному уравнению (30) и принимает на границе заданные значения.

В качестве примера рассмотрим решение уравнения Лапласа u_xx + u_yy = 0 вида:

В качестве области интегрирования выберем единичный квадрат, т.е. G(x,y) = [0,1] 2 . Учитывая (34), определим граничные условия для задачи Дирихле

(35)

Определим квадратную сетку в единичном квадрате: x_n = h(n -1), y_m = h(m — 1), h = 1/(N — 1), n,m = 1,…,N. Регулярными и нерегулярными (граничными) будут соответственно узлы

, (36)

(36¢)

Найдем решение уравнения Лапласа (34) задачи Дирихле (35) методом Монте-Карло. Разыграем случайный процесс следующим образом. Выберем произвольный регулярный узел P из набора (36). Выпустим из этого узла частицу, и дождемся когда она, путем случайного блуждания, попадет в одну из граничных точек (36¢). Повторим эту процедуру R раз, запоминая число приходов L(P,Q) частицы в граничные точки (36¢). В итоге можно получить следующую расчетную схему:

. (37)

На листинге_№12 приведен код программы решения уравнения Лапласа (34) для задачи Дирихле в единичном квадрате (35) по расчетной схеме (37).

%Программа решения уравнения Лапласа, имеющего

%аналитическое решение (34) для задачи Дирихле

%в единичном квадрате (35) по расчетной схеме

%(37) методом Монте-Карло

%Определяем количество N узлов в сетках по

%координатам x и y

%Определяем сетки по координатам х и у

%Вносим краевые условия (35) для задачи Дирихле

%Определяем массив статистических испытаний с

%Организуем цикл статистических испытаний с разной

%длиной статистических испытаний

%Цикл статистических испытаний для каждой

%регулярной точки разностной сетки

%Определяем четыре массива для

%четырех типов граничных точек

%единичного квадрата: нижнее

%основание, правая сторона,

%верхнее основание, левая

%Статистические испытания длиной R(s)

%Цикл, моделирующий случайные

%блужданий на решетке

while (Pn>1)&(Pn 1)&(Pm 0.25)&(rnd 0.5)&(rnd 0.75

источники:

http://cyberleninka.ru/article/n/algoritm-monte-karlo-dlya-resheniya-sistem-lineynyh-algebraicheskih-uravneniy-metodom-zeydelya

http://poisk-ru.ru/s12823t3.html