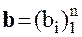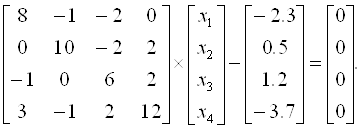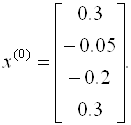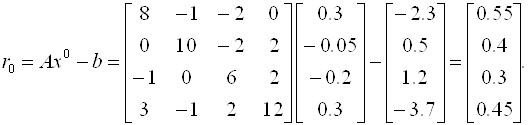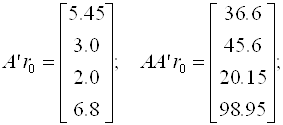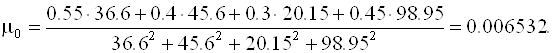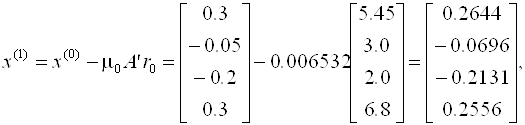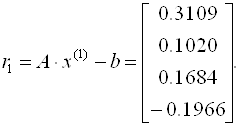Решение систем линейных алгебраических уравнений
Страницы работы
Содержание работы
Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Решить систему линейных алгебраических уравнений (САУ)
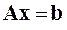
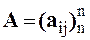
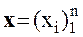
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на 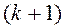
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
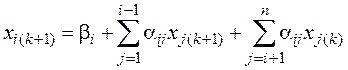
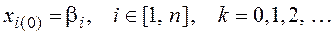
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
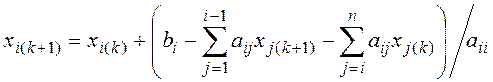
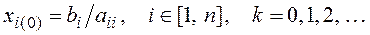
Если матрица 
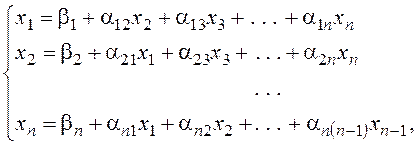
где 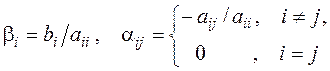


Из неособенной матрицы 

Метод наискорейшего спуска. Данный метод относится к группе нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в которых осуществлялось по отдельным координатам, предполагают траекторию движения к истинному решению сразу по всем координатам по линии наискорейшего спуска в направлении, противоположном вектору градиента функционала, связанного с ошибкой между истинным решением и решением на 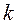
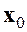
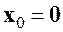
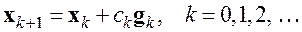
где 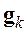
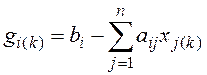
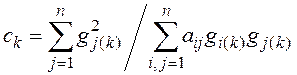
Чтобы упростить процедуру определения вектора невязки, особенно при больших порядках 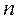
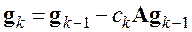
Однако из-за наличия вычислительных погрешностей векторы 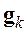
Если матрица 
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) — (N ´ N)-мерная матрица САУ;
B(N) — N-мерный вектор правой части САУ;
N — мерность САУ;
G(N) — N-мерный вектор невязки (g = b — Ax);
X(N) — N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) — N-мерный вектор уточненных значений решения САУ.
Окончание итерационной процедуры производиться при выполнении условия 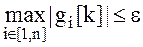
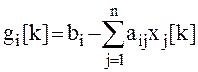
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).
Представим систему линейных уравнений в следующем виде:
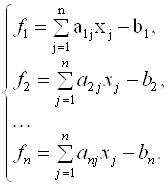
Запишем выражение (3.38) в операторной форме:
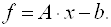
Здесь приняты следующие обозначения:
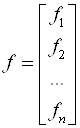
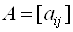

В методе скорейшего спуска решение ищут в виде
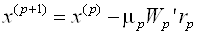
Где 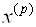
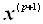
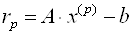
А 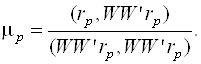
В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:
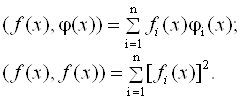
В формуле (3.43) 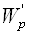

Нетрудно убедиться, что для системы (3.39) матрица Якоби равна

Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять 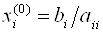
· Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации.
· Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.
· В методе градиента итерационный процесс естественно закончить при достижении 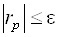
· В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.
· Итерационный процесс можно прервать на любом K–ом шаге и продолжить позднее, введя в качестве нулевого шага значения X(K).
· В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.
Пример 3.7. Методом скорейшего спуска решим систему уравнений
Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:
Следовательно, вектор невязок на нулевом шаге равен
Далее последовательно вычисляем
Отсюда
Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).
Вопросы для самопроверки
· Назовите известные вам методы решения СЛАУ.
· Чем точные методы отличаются от приближенных?
· Что такое прямой и обратный ход в методе Гаусса?
· Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя?
· Что такое невязка?
· Сравните достоинства и недостатки точных и приближенных методов.
· Что такое матрица Якоби?
· Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента?
· Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения
А) начального приближения (нулевой итерации);
Б) первой итерации?
· При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?
Итерационные методы решения систем линейных алгебраических уравнений
Стандартные итерационные методы
В разделах Метод исключения Гаусса и Методы решения систем с симметричными матрицами процедуры решения систем алгебраических уравнений были связаны с разложением матрицы коэффициентов \( A \). Методы такого типа называются прямыми методами. Противоположностью прямым методам являются итерационные методы. Эти методы порождают последовательность приближенных решений \( \ < x^<(k)>\> \). При оценивании качества итерационных методов в центре внимания вопрос от том, как быстро сходятся итерации \( x^ <(k)>\).
Итерации Якоби и Гаусса — Зейделя
Простейшей итерационной схемой, возможно, являются итерации Якоби. Они определяются для матриц с ненулевыми диагональными элементами. Идею метода можно представить, используя запись \( 3 \times 3 \)-системы \( Ax = b \) в следующем виде: $$ \begin
Эти формулы и определяют итерации Якоби в случае \( n = 3 \). Для произвольных \( n \) мы имеем $$ \begin
Заметим, что в итерациях Якоби при вычислении \( x_i^ <(k+1)>\) не используется информация, полученная в самый последний момент. Например, при вычислении \( x_2^ <(k+1)>\) используется \( x_1^ <(k)>\), хотя уже известна компонента \( x_1^ <(k+1)>\). Если мы пересмотрим итерации Якоби с тем, чтобы всегда использовать самые последние оценки для \( x_i \), то получим: $$ \begin
Для итераций Якоби и Гаусса — Зейделя переход от \( x^ <(k)>\) к \( x^ <(k+1)>\) в сжатой форме описывается в терминах матриц \( L, D \) и \( U \), определяемых следующим образом: $$ \begin
Процедуры Якоби и Гаусса — Зейделя — это типичные представители большого семейства итерационных методов, имеющих вид $$ \begin
Сходятся ли итерации (9) к \( x = A^<-1>b \), зависит от собственных значений матрицы \( M^<-1>N \). Определим спектральный радиус произвольной \( n \times n \)-матрицы \( G \) как $$ \rho(G) = \max \< |\lambda| :\ \lambda \in \lambda(G) \>, $$ тогда если матрица \( M \) невырожденная и \( \rho(M^<-1>N) —>
http://matica.org.ua/metodichki-i-knigi-po-matematike/chislennye-metody-iu-ia-katcman/3-8-metod-skoreishego-spuska-gradienta-dlia-sluchaia—sistemy-lineinykh-algebraicheskikh-uravnenii
http://slemeshevsky.github.io/num-mmf/sles/html/._sles-FlatUI002.html