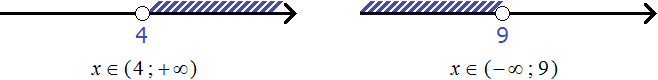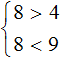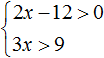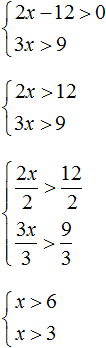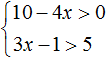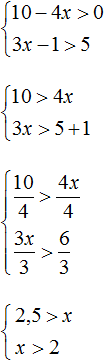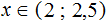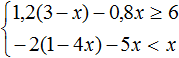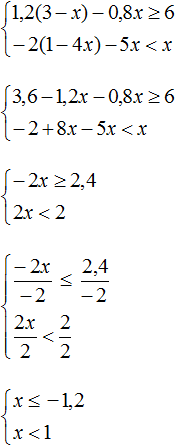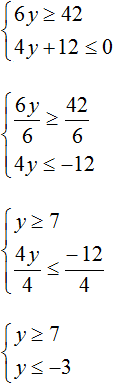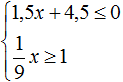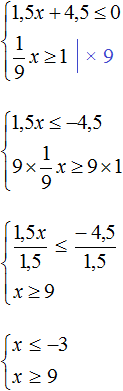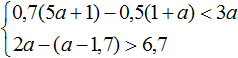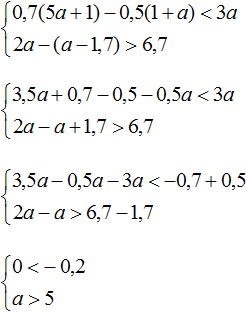Решение системы уравнений неравенств с одной переменной

Системы линейных неравенств с одной переменной

Примеры решения систем линейных неравенств с одной переменной

Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.

Рассмотрим простейший пример. Система 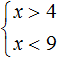состоит из двух неравенств, которые уже решены.

Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.

Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:

Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями как им захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.

Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.

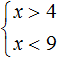
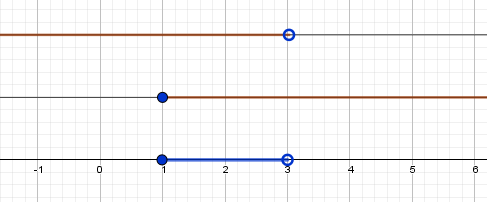
Значит решениями системы являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x строгие. Ответ можно записать в виде числового промежутка:

Также, нужно изобразить множество решений системы на координатной прямой.

Для системы линейных неравенств решение на координатной прямой изображают так:

Сначала указывают границы обоих неравенств:

На верхней области отмечают множество решений первого неравенства x > 4

На нижней области отмечают множество решений второго неравенства x (4; 9) , например, число 8

Видим, что решение 8 удовлетворяет обоим неравенствам.

Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:

Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.

Пример 2. Решить систему неравенств

Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.

Решениями же обоих неравенств являются все числа, которые больше 17.

Изобразим множество решений системы 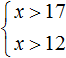на координатной прямой и запишем ответ в виде числового промежутка.

Для начала отметим на координатной прямой границы обоих неравенств:

На верхней области отметим множество решений первого неравенства x > 17

На нижней области отметим множество решений второго неравенства x > 12

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 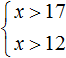. Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок

Получили систему 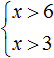. На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.

Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы

Пример 4. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений системы 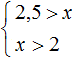на координатной прямой и запишем ответ в виде числового промежутка:

Пример 5. Решить неравенство

Решим каждое неравенство по отдельности:

Изобразим множество решений системы 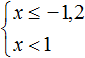на координатной прямой и запишем ответ в виде числового промежутка:

Когда решений нет

Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.

Пример 1. Решить неравенство

Решим каждое неравенство по отдельности:

Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.

Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:

На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система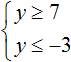

Ответ: решений нет.

Пример 2. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:

Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система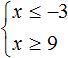

Ответ: решений нет.

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности:

Получили неравенства 0 и a > 5 . Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a , то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система

Решение систем неравенств с одной переменной

Понятие системы неравенств с одной переменной и его решения

Несколько неравенств с одной переменной образуют систему , если нужно найти такое множество значений переменной, которое будет решением каждого из неравенств.

Решением системы неравенств с одной переменной является такое множество значений этой переменной, которое превращает каждое из неравенств в верное числовое неравенство.

Следствие: общим решением системы неравенств с одной переменной является пересечение частных решений каждого из неравенств системы .

Например: $<\left\< \begin x+7 \ge 2 \\ x-4 \lt 1 \end \right.> \iff <\left\< \begin x \ge -5 \\ x \lt 5 \end \right.> \iff -5 \le x \lt 5 или x \in \Bbb[-5;5)$ — полуинтервал

Алгоритм решения системы неравенств с одной переменной

Подробно о числовой прямой и видах числовых промежутков на ней рассказано в §16 данного справочника. Здесь мы изобразим числовые промежутки как решения неравенств на более простых примерах.

Шаг 1. Найти множество частных решений для каждого из неравенств системы. Если хотя бы одно из частных решений является пустым множеством, вся система неравенств не имеет решений; перейти к шагу 4.

Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать .

Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их пересечение – это и будет общим решением системы .

Шаг 4. Работа завершена.

Например: $<\left\< \begin x-2 \lt 1 \\ x+5 \ge 6 \end \right.> \iff <\left\< \begin x \lt 3 \\ x \ge 1 \end \right.> \iff 1 \le x \lt 3 или x \in \Bbb[1;3)$ — полуинтервал

Если в системе неравенств есть несколько неравенств со знаком «больше», то из них останется одно неравенство по принципу «больше большего».

Если в системе неравенств есть несколько неравенств со знаком «меньше», то из них останется одно неравенство по принципу «меньше меньшего» .

1) В системе $ <\left\< \begin x \gt 5 \\ x \gt 2 \\ x \gt 3 \end \right.> $ наибольшее число (условие) справа 5.

По принципу «больше большего» останется: $ <\left\< \begin x \gt 5 \\ x \gt 2 \\ x \gt 3 \end \right.> \iff x \gt 5 $

2) В системе $ <\left\< \begin x \lt 5 \\ x \lt 2 \\ x \lt 3 \end \right.> $ наименьшее число (условие) справа 2.

По принципу «меньше меньшего» останется: $ <\left\< \begin x \lt 5 \\ x \lt 2 \\ x \lt 3 \end \right.> \iff x \lt 2 $

Примеры

Пример 1. Решите системы уравнений:

$а) <\left\< \begin 2(x-8) \ge x-16 \\ 3(x+1) \le 11 \end \right.> \iff <\left\< \begin 2x-x \ge -16+16 \\ 2x \le 11-3 \end \right.> \iff <\left\< \begin x \ge 0 \\ 2x \le 8 \end \right.> \iff <\left\< \begin x \ge 0 \\ x \le 4 \end \right.> \iff 0 \le x \le 4$

$x \in [0;4]$ — интервал

$б) <\left\< \begin 5(x-6) \gt x-10 \\ 4(x-1) \lt x+5 \end \right.> \iff <\left\< \begin 5x-x \gt 30-10 \\ 4x-x \lt 5+4 \end \right.> \iff <\left\< \begin 4x \gt 20 \\ 3x \lt 9 \end \right.> \iff <\left\< \begin x \gt 5 \\ x \lt 3 \end \right.> \iff x \in \varnothing$

$x \in \varnothing$ — решений нет

$в) <\left\< \begin -5 \lt 3x+1 \le 4 \\ 3 \lt 2x+5 \lt 9 \end \right.> \iff <\left\< \begin -5-1 \lt 3x \le 4-1 \\ 3-5 \lt 2x \lt 9-5 \end \right.> \iff <\left\< \begin -6 \lt 3x \le 3 \\ -2 \lt 2x \lt 4 \end \right.> \iff <\left\< \begin -2 \lt x \le 1 \\ -1 \lt x \lt 2 \end \right.> \iff$

$$\iff -1 \lt x \le 1$$

$x \in (-1;1] $ — полуинтервал

Пример 2. При каких значениях переменной x имеет смысл выражение:

$ <\left\< \begin x+2 \ge 0 \\ 4-x \ge 0 \end \right.> \iff <\left\< \begin x \ge -2 \\ x \le 4 \end \right.> \iff -2 \le x \le 4 $

$x \in [-1,5;4) \cup (4;+ \infty) $

$ <\left\< \begin x-5 \gt 0 \\ 1-x \gt 0 \end \right.> \iff <\left\< \begin x \gt 5 \\ x \lt 1 \end \right.> \iff x \in \varnothing$

$x \in \varnothing $ — решений нет

Пример 3*. У космического пирата Шутзема несколько затруднительное финансовое положение и только 510 астротугриков в кармане. Однако ему нужно пополнить запасы топлива и продовольствия. Одна капсула с топливом стоит 50 астротугриков, а одна капсула с едой – 30 астротугриков. Какой вариант покупок есть у Шутзема на всю сумму без сдачи, если топлива нужно не менее 4 капсул, а еды – не менее 5?

Пусть x — количество капсул с топливом, y – количество капсул с едой.

По условию задачи:

$$ <\left\< \begin 50x+30y \le 500 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end \right.> \iff <\left\< \begin 5x+3y \le 50 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end \right.> $$

Изобразим полученные полуплоскости графически и найдём их пересечение.

Прямая сверху – это бюджетное ограничение.

На этой прямой в области допустимых значений (закрашенный треугольник, стороны включительно) есть только одно целое решение: $ <\left\< \begin x = 6 \\ y = 7 \end \right.> $

Ответ: 6 капсул топлива и 7 капсул еды.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение систем неравенств: линейные, квадратные и дробные.

Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).

Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5y +1/7y^2
Результат: \( 3\frac<1> <3>— 5\frac<6> <5>y + \frac<1><7>y^2 \)

При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Выберите нужный знак неравенства и введите многочлены в поля ниже.