Решение системы уравнений относительно переменной

Решение системы уравнений относительно переменной

В этом разделе обсуждается, как в символьном виде решать уравнения и системы уравнений. Команда Решить относительно переменной из меню Символика позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

В этом разделе описывается также, как в символьном виде решить систему уравнений, используя блоки решения уравнений. Для этого требуется Mathcad PLUS.

Решать уравнение символьно гораздо труднее, чем численно. Может оказаться, что в символьном виде решение не существует. Это может быть вызвано рядом причин, обсуждаемых в разделе “Ограничения символьных преобразований”.

Решение уравнения относительно переменной

Чтобы решить уравнение относительно переменной:

• Напечайте уравнение. Убедитесь, что для выведения знака равенства использована комбинация клавиш [Ctrl]=.
• Выделите переменную, относительно которой нужно решить уравнение, щёлкнув на ней мышью.
• Выберите Решить относительно переменной из меню Символика

Mathcad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ. Обратите внимание, что, если переменная возводилась в квадрат в первоначальном уравнении, при решении можно получить два ответа. Mathcad отображает их в виде вектора. Рисунок 20 показывает соответствующий пример.

Рисунок 20: Преобразование выражения для решения уравнения.

Можно также решать неравенство, использующее символы , и . Решения для неравенств будут отображаться в терминах булевых выражений Mathcad. Если имеется более одного решения, Mathcad помещает их в вектор. В Mathcad булево выражение типа x

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Использование метода Given — Find:

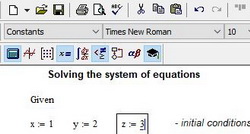
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

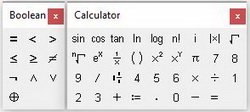
Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

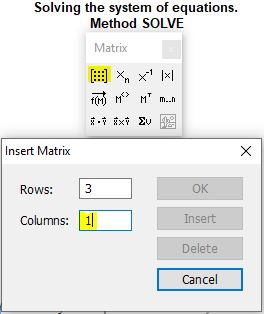
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается: