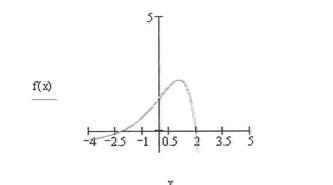
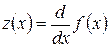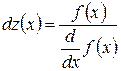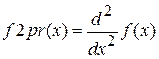Решение скалярных уравнений методом итераций

Метод итераций

Правила ввода функции

Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).

Достаточные условия сходимости метода итерации

Процесс нахождения нулей функции методом итераций состоит из следующих этапов:

Получить шаблон с омощью этого сервиса.
Уточнить интервалы в ячейках B2 , B3 .
Копировать строки итераций до требуемой точности (столбец D ).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .

Численные методы решения скалярных уравнений

Цель работы:сформировать у студентов представление о применении уравнений в различных областях деятельности, привить знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения и выбора того или иного программного средства для проверки правильности найденного результата.

Метод хорд

Решить уравнение е х ∙ (2 – х) – 0,5 = 0 методом хорд с точностью ɛ = 0,001.

1. Отделяем корни.Этот этап решения осуществляется с помощью аналитического или графического метода. После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана любая точка [a,b] (начало отрезка, его середина и т.д.).

Воспользуемся графическим методом. Построим график функций и найдем точки пересечения его с осью Ох (рис.2.1.).

f(x) = (2 – x) (e x ) – 0,5

Рис.2.1. Отделение корней графически

Получили два интервала: [-3; -2], [1,5; 2,5]. Интервал, в котором мы будем уточнять корень – [1,5; 2,5].

2. Уточняем корни. Находим первую производную функции

3. Определяем знакиf(x) на отрезке [1,5; 2,5]:

f(1,5) = 1,741>0, f(2,5) = -6,591 8,801∙ 10 -4 ), значит х₈ = 1,927 является решением нашего уравнения.

п = 0. 10

х₀=а

Рис. 2.2. Проверка критерия достижения

5. Создаем функцию, реализующую вычисления корня уравнения

е х ∙ (2 – х) – 0,5 = 0 на отрезке [1,5; 2,5] с точностью ɛ = 0,001 методом хорд (рис. 2.3). Решением будет являться число 1,927, получившееся на третьем шаге решении

Рис.2.3. Функция, возвращающая значения корня уравнения методом хорд.

Аргументы функции: а, b – концы отрезка; 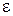– погрешность вычислений,

f 1pr(x) – функция первой производной

6. Проверяем решение уравнения встроенными функциями Матhcad

хl = root(f(x),x) xl = 1,927

(2 – x)∙(e X ) – 0,5 = 0

x2 = Find(x) x2 = 1,927

Метод касательных

Пример 2.2.

Вычислить методом касательных корень уравнения е х ∙(2 – х) –0,5=0 на отрезке[1,5; 2,5] с точностью ɛ = 0,001.

Решение.

1. Отделяем корни уравнения (см. разд. 2.1).

2. Определяем неподвижную точку.

Для этого определим знаки функции и второй производной на отделенном интервале [1,5; 2,5]. Для этого составим функцию, проверяющую условие неподвижности точки

f(x) = (2 – x)(e x ) – 0,5

Тогда подвижной точкой будет точка а = 1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных (рис. 2.4).

х₀ = а

Рис. 2.4.Построение итерационной последовательности

по методу касательных

Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение

х₄ = 1,927 при п = 4, т.к. 2,367∙10 -5 ˂ 0,001.

4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).

5. Проверяем полученные результаты.

Отметим, что в пакете Mathcad имеется еще несколько функций, позволяющих решать уравнения, например, функция solve, вызываемая с панели Symbolic (рис. 2.5.)

Рис. 2.5. Панель Symbolic

Пример использования команды solve представлен на рис. 2.6.

Рис.2.6. Решение уравнения с помощью команды solve

Метод простой итерации

Пример 2.3.

Решить уравнение 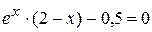методом простой итерации с точностью ɛ = 0,001.

Решение.

Схема решения уравнения методом простой итерации следующая.

1. Отделяем корни.

2. Приводим исходное уравнение к виду х = f(х).

Заменим уравнение 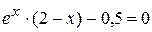уравнением вида .

Здесь величина m должна быть подобрана так, чтобы для функции f(x) выполнились условия 2 и 3 теоремы о достаточном условии сходимости итерационного процесса.

Производная Fˈ(х) на отрезке [1,5; 2,5] отрицательна, следовательно, функция F(х) на этом отрезке монотонно убывает. Ее значения представлены на рис. 2.7.

1,7408
1,4812
1,1422
0,7099
0,1686
-0,5
-1,3166
-2,305
-3,4923
-4,9093
-6,5912

Рис. 2.7.Значение функции

на отрезке [1,5; 2,5]

Тогда значения функции f(x) будут равны:

Учитывая монотонность функции f(x), из последних равенств легко заметить, что условие 2 указанной теоремы будем заведомо выполнено, если m – правильная отрицательная дробь (рис. 2.8).

Рис.2.8.Определение значения m

Поскольку производная Fˈ(x) на концах интервала [1,5; 2,5] положительна (Fˈ(1,5) = 2,241, Fˈ(2,5) = 18,274) и монотонно возрастает, ее модуль имеет максимум на правом конце отрезка. Тогда если за m принять число , то для любого х из отрезка [1,5; 2,5] значение выражения будет правильной отрицательной дробью. Это обеспечивает выполнение условия 2 теоремы (рис.2.9.).

Для выполнения условия 3 указанной выше теоремы 2.2 найдем производную преобразованной функции

и ее значения на концах отрезка [1,5; 2,5].

Условие 3 теоремы выполнено: значения производных меньше единицы. За величину q возьмем число 0,877 (рис. 2.9.).

Рис. 2.9.Определение значения q

3. Вычисляем значения итерационной последовательности .

В качестве начального значения возьмем, например, начало отрезка, точку х₀ = 1,5.

Критерием достижения заданной точки ɛ = 0,001 при решении нашего уравнения методом простой итерации является величина, равная 1,398∙10 -5 (рис. 2.10).

Рис. 2.10.Определение критерия достижения

заданной точности q

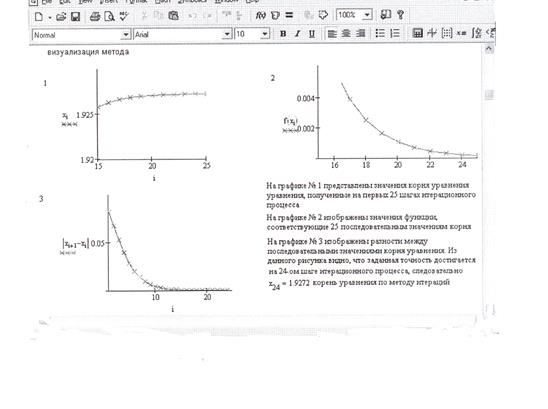
4. Строим итерационную последовательность (рис. 2.11).

x_i = z(x_i_-1)

Рис. 2.11.Построение итерационной последовательности

по методу простой итерации

Для 24-го приближения получили, что ˂ 1,398∙ 10 -5 ˂А. Отсюда следует, что х₂₃ = 1,92718 является приближенным решением нашего уравнения.

5. Создаем функцию, реализующую метод простой итерации, для решения уравнения x = f(x) по методу простой итерации (составляется аналогично рассмотренным выше методам).

6. Визуализируем решение уравнения методом простой итерации (рис. 2.12).

Рис. 2.12. Визуализация решения уравнения F(x) = (2 – x)∙e x – 0,5

Вопросы по теме

1. Что значит решить уравнение?

2. Каковы этапы решения уравнения с одной неизвестной численными методами?

3. Какие существуют методы решения с одной неизвестной?

4. В чем заключается этап отделения корней при использовании численных методов решения уравнения?

5. Суть метода хорд. Графическая интерпретация метода.

6. Суть метода касательных. Графическая интерпретация метода.

7. Суть метода простой итерации.

8. Какое уравнение можно решать методом простой итерации?

9. Каковы достаточные условия сходимости итерационного процесса при решении уравнения x = f(x) на отрезке [a, b], содержащего корень, методом простой итерации?

10. Какое условие является критерием достижения заданной точности при решении уравнения x = f(x) методом хорд, касательных, итерацией?

11. Записать формулу нахождения значений последовательности при решении уравнения методом: хорд, касательных.

12. Как строится итерационная последовательность точек при решении уравнения методом простой итерации?

Решение скалярных уравнений методом итераций

Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁== 0.268;

X₂== 3.732;

Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.