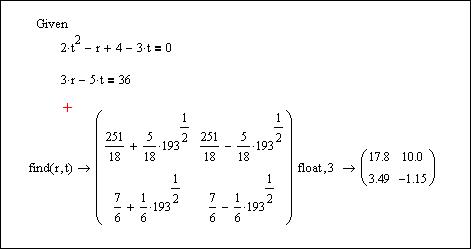Решение систем трансцендентных уравнений
К настоящему времени разработано много методов решения систем уравнений. Для решения систем уравнений в системе MathCad предусмотрен, так называемый, блок решения. Он удобен тем, что при его использовании уравнения записываются в обычной форме, а также тем, что позволяет решать как системы линейных, так и системы нелинейных уравнений, причем, как в численном, так и символьном виде.
Последовательность действий при численном решении сводится к следующему:
Задаются начальные значения для искомых переменных.
Формируется блок решения, а именно: между ключевыми словами Given и find(список искомых переменных) записывается система уравнений. Напомним, что знак «=» при написании уравнений выделен цветом. Это – булевский знак! Его следует брать с панели Boolean.
После конструкции find записывается знак «=».
При символьном решении задание начальных значений не требуется, а вместо знака «=» для решения следует использовать знак «®».
Пример 15. Требуется найти точки экстремума функции 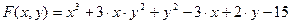
Решение. Известно, что необходимым условием для существования экстремума – равенство нулю частных производных первого порядка. Поэтому на начальном этапе необходимо получить частные производные по переменной x и по переменной y и приравнять их нулю. Для вычисления производной можно воспользоваться соответствующей командой панели Calculus(Вычислить). После чего процесс решения задачи можно свести к процессу решения системы уравнений. На рис. 6.17 представлены фрагменты документа MathCAD, содержащие поиск экстремумов функции.
 a) a) | 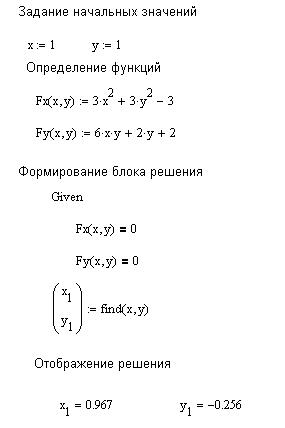 b) b) |
Рис. 6.17. Решение системы нелинейных уравнений в
задаче поиска экстремума
На рис. 6.17 представлены два варианта записи решения. На фрагменте, представленном на рис. 6.17, а, системы записаны в развернутом виде, а на рис. 6.17, b частные производные оформлены в виде функций и результаты решения заносятся в векторные значения.
Пример 16. Требуется найти точки пересечения параболы, заданной уравнением 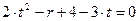
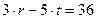
Решение. Предоставим два варианта решения задачи:
решение с использованием блока решения;
решение в графическом виде.
Вариант а
Поскольку точки пересечения линий являются общими для этих линий, то для определения точек пересечения следует решить систему из двух уравнений, описывающих эти линии. Если воспользоваться символьным блоком решения, то точки пересечения могут быть получены в виде, как это показано на рис. 6.18.
Рис. 6.18. Решение системы нелинейных уравнений в
задаче поиска экстремума
Поскольку используется символьный блок решения, для представления результатов в числовом виде используется команда float. Анализ полученных результатов показывает, что заданные линии пересекаются в двух точках с координатами (r, t) – (17.8, 3.49) и (10.0, –1.15).
Вариант b
Для получения графического решения представим уравнения линий в виде функций от одной из переменных. В качестве независимой переменной выберем переменную t, т.к. переменная r в данном случае входит в оба уравнения в первой степени. В результате придем сначала к двум уравнениям вида: 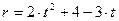
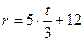
Изменение независимой переменной на начальном этапе будет взято «по умолчанию». Для уточнения координат точек пересечения выполняются следующие действия:
переустанавливаются на графике диапазоны для изменения x и y;
включается режим трассировки, путем щелчка правой кнопкой мыши на графике, выбор команды Trace… (Трассировка . );
активизирует окно с координатами трассировки – щелчок левой кнопкой мыши на графике;
появившиеся координатные оси можно перемещать по графику от одной точки пересечения до другой.
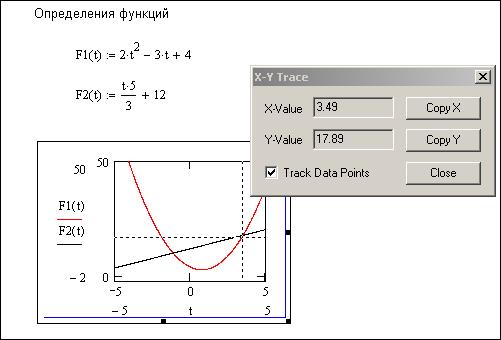
На рис. 6.19 приведен фрагмент документа с графическим решением задачи – получение точек пересечения двух линий в декартовой системе координат.
Рис. 6.19. Решение системы нелинейных уравнений в
задаче поиска экстремума
Анализ решений показывает, что результаты решений, произведенных разными способами, совпадают между собой.
При анализе систем нелинейных алгебраических уравнений важным обстоятельством явялется графическое построение систем функций.
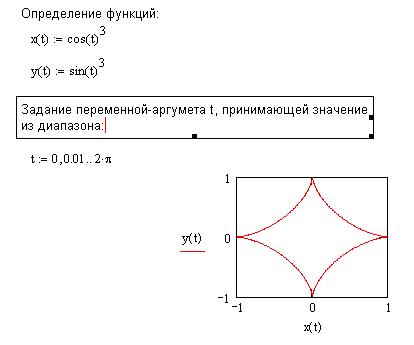
Пример 17. Требуется построить график функции, заданной в параметрическом виде: 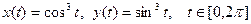
Решение. Для построения графика функции, заданной в параметрическом виде, сначала нужно выбрать шаблон двумерного графика
X-Y Plot, в середине горизонтальных и вертикальных осей ввести функции Переменная может быть задана, как индексированная переменная. На рис. 6.20 представлены результаты построения требуемой функции.
Рис. 6.20. График сложной функции, заданной парметрически
Глава 7
ОПЕРАЦИИ С ВЕКТОРАМИ И МАТРИЦАМИ, МАТРИЧНЫЕ ФУНКЦИИ
В МАТЕМАТИЧЕСКОМ ПАКЕТЕ MATHCAD
Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).
Матричные вычисления в MathCAD можно условно разделить на три основных типа.
К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) и Symbolics (Символьные).
Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.
И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.
В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.
Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: 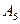
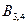
Для заданияиндексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.
Дата добавления: 2015-01-10 ; просмотров: 1008 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. МЕТОДЫ РЕШЕНИЯ
Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
1) Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.
2) Значения f(x) на концах отрезка имеют разные знаки (f(a)×f(b) (x) сохраняют определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a,b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.
Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.
Всякое значение 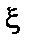
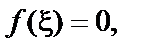 |
называется корнем уравнения (1) или нулем функции f(x).
Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:
1) отделение корней — отыскание приближенного значения корня или содержащего его отрезка;
2) уточнение приближенных корней — доведение их до заданной степени точности.
Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.
Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.
В инженерной практике распространен графический способ определения приближенных корней.
Графический метод отделения корней
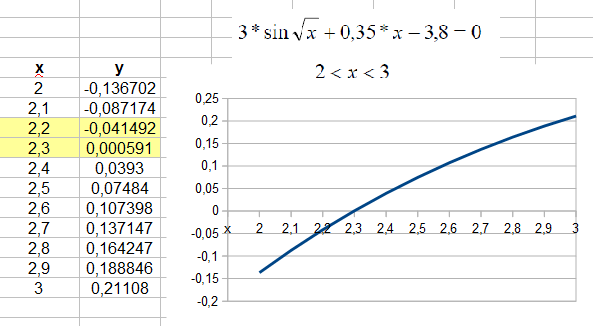
Для отделения корня графическим способом строится график функции f(x)=0 по таблице значений аргументов и функций, где аргумент изменяется с фиксированным шагом. Визуально определяют точку пересечения графика с осью OX. На этом интервале функция меняет знак отрицательный на положительный (рис.1).
Рис.1. Отделение корня графическим способом
Этот интервал изолируют как интервал с единственным возможным корнем. Уравнение может иметь несколько интервалов изоляций и, соответственно, несколько корней.
Рассмотрим методы уточнения приближенных корней в электронной таблице Calc. Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
1. подбора параметра;
2. метод простых итераций;
3. метод половинного деления (метод дихотомии);
4. метод Ньютона (метод касательных);
5. модифицированный метод Ньютона (метод секущих);
6. метод хорд и др.
Подбор параметра
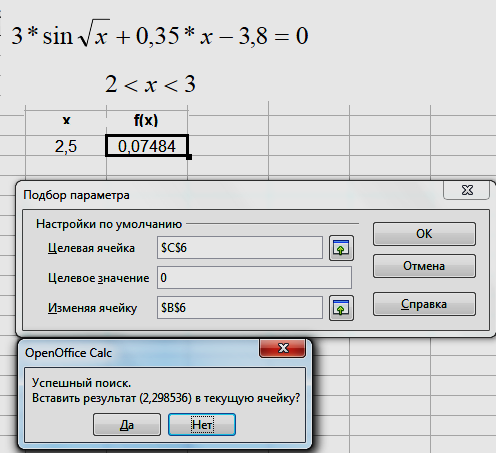
При подборе параметра OOo Calc изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат. Для реализации этого метода нужно в любую ячейку таблицы ввести значение х, принадлежащее интервалу [а,b] (т.е., в пределах отделенного корня). В следующую ячейку ввести значение функции f(x). Затем выбрать команду Сервис\Подбор параметра (рис.2.). В появившемся окне подбора параметра ввести:
• Ячейка с формулой – адрес ячейки с уравнением.
• Целевое значение – результат функции.
• Изменяемая ячейка – адрес ячейки, в которой находится переменная, т.е. х подбираемый из диапазона.
Программа Calc подбирает наиболее подходящий корень и вставляет его в изменяемую ячейку, т.е. вместо х.
Пример решения уравнения методом подбора параметра показан на рис.2.
Рис.2. Метод побора параметра
Дата добавления: 2016-06-15 ; просмотров: 13724 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://poznayka.org/s14347t1.html