Метод итераций
Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Решение трансцендентных уравнений методом простых итераций
Исходное уравнение (3.1) преобразуем к эквивалентному уравнению:
x =  (x). (x). | (3.8) |
Пусть известно начальное приближение (полученное, например, на этапе отделения корней): x = x 0. Подставим его в правую часть (3.8) и получим новое приближение: x1 = 
xk = 
В качестве условия окончания вычислительного процесса можно взять выполнение неравенства: ½xk — xk-1½ * — истинное, искомое значение корня; x0 — начальное приближение к корню; x1, x2, x3 — очередные итерации.
 Рис.3.8. Рис.3.8. |  Рис.3.9. Рис.3.9. |
При использовании этого метода возникает вопрос о его сходимости. Дело в том, что при некоторых условиях расстояние между истинным корнем и приближениями к нему может возрастать с каждой новой итерацией, как это показано на рис.3.10, 3.11.
 Рис.3.10. Рис.3.10. | 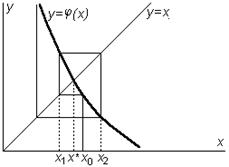 Рис.3.11. Рис.3.11. |
Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства:
½  (x)½ . F(x) = 0 (x)½ . F(x) = 0 | Þ | C . F(x) + x = x | (3.15) |
Здесь C — некоторый параметр, выбираемый из условия сходимости процесса.
При использовании преобразования (3.15) условием окончания вычислительного процесса является выполнение неравенства


В программе необходимо указывать функцию F(x) и вводить вычисленный заранее параметрС и значение допустимой погрешности 
РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. МЕТОДЫ РЕШЕНИЯ
Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
1) Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.
2) Значения f(x) на концах отрезка имеют разные знаки (f(a)×f(b) (x) сохраняют определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a,b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.
Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.
Всякое значение 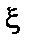
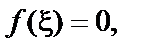 |
называется корнем уравнения (1) или нулем функции f(x).
Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:
1) отделение корней — отыскание приближенного значения корня или содержащего его отрезка;
2) уточнение приближенных корней — доведение их до заданной степени точности.
Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.
Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.
В инженерной практике распространен графический способ определения приближенных корней.
Графический метод отделения корней
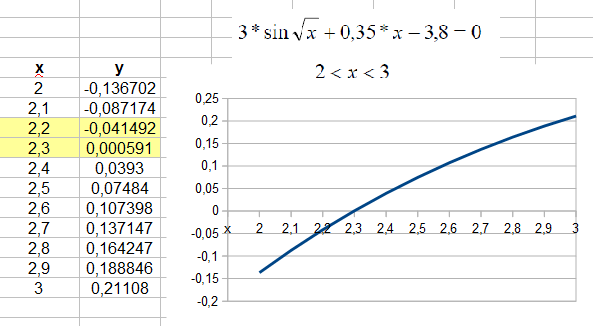
Для отделения корня графическим способом строится график функции f(x)=0 по таблице значений аргументов и функций, где аргумент изменяется с фиксированным шагом. Визуально определяют точку пересечения графика с осью OX. На этом интервале функция меняет знак отрицательный на положительный (рис.1).
Рис.1. Отделение корня графическим способом
Этот интервал изолируют как интервал с единственным возможным корнем. Уравнение может иметь несколько интервалов изоляций и, соответственно, несколько корней.
Рассмотрим методы уточнения приближенных корней в электронной таблице Calc. Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
1. подбора параметра;
2. метод простых итераций;
3. метод половинного деления (метод дихотомии);
4. метод Ньютона (метод касательных);
5. модифицированный метод Ньютона (метод секущих);
6. метод хорд и др.
Подбор параметра
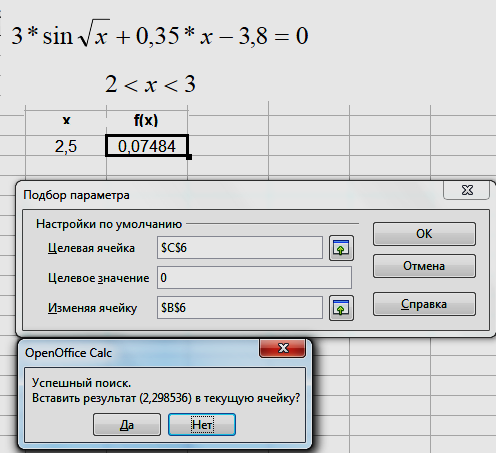
При подборе параметра OOo Calc изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат. Для реализации этого метода нужно в любую ячейку таблицы ввести значение х, принадлежащее интервалу [а,b] (т.е., в пределах отделенного корня). В следующую ячейку ввести значение функции f(x). Затем выбрать команду Сервис\Подбор параметра (рис.2.). В появившемся окне подбора параметра ввести:
• Ячейка с формулой – адрес ячейки с уравнением.
• Целевое значение – результат функции.
• Изменяемая ячейка – адрес ячейки, в которой находится переменная, т.е. х подбираемый из диапазона.
Программа Calc подбирает наиболее подходящий корень и вставляет его в изменяемую ячейку, т.е. вместо х.
Пример решения уравнения методом подбора параметра показан на рис.2.
Рис.2. Метод побора параметра
Дата добавления: 2016-06-15 ; просмотров: 13692 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://lektsii.org/1-4780.html
http://poznayka.org/s14347t1.html
 ≡ x^2/(1+x)
≡ x^2/(1+x)