Решение тригонометрических уравнений и неравенств(подготовка к ЕГЭ)
презентация к уроку по алгебре (11 класс) по теме
Рассмотрены способы решения тригонометрических уравнений и неравенств
Скачать:
| Вложение | Размер |
|---|---|
| Решение тригонометрических уравнений и неравенств | 1.43 МБ |
| reshenie_trigonometricheskih_uravneniy_-2.ppt | 1.68 МБ |
Предварительный просмотр:
Подписи к слайдам:
Предварительный просмотр:
Подписи к слайдам:
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
№ Уравнения № метода Методы 1 Sin x/3 — cos 6x = 2 4(б) 1.Разложение на множители. 2.Введение новой переменной: а) сведение к квадратному; б) универсальная подстановка; в) введение вспомогательного аргумента. 3. Сведение к однородному уравнению. 4. Использование свойств функций, входящих в уравнение: а) обращение к условию равенства тригонометрических функций; б) использование свойства ограниченности функции. 2 3 4 5 sinx – 2 cosx = 1 3, 2(б,в) 5 sin3x cos2x = 1 4(б) 6 cos2x = (cos x – sin x ) 1,2(б,в),3 7 1 – sin2x = cos x – sin x 1,2(б,в)3 8 cos3x = sin x 4(а) 9 4 – cos 2 x = 4 sin x 2(а) 10 sin3x – sin5x = 0 4(б) 11 tg 3x tg(5x + /3) = 1 4(а) 12 2 tg x/2 — cos x = 2 1,2(а,б,в),3,4(а)
1. Какие методы решения тригонометрических уравнений вы знаете? 2. Определите и ответьте, какими методами нужно решать данные тригонометрические уравнения? а ) sin 2x – cos x = 0 б ) 2sin²x — 5sinx = -3 в ) cos²x – sin²x = sinx – cosx г ) sin2 x – 3sinx cosx + 2cos²x = 0 3. Решите простейшие тригонометрические уравнения:
Некоторые типы тригонометрических уравнений . Уравнения, сводящиеся к квадратным, относительно cos х = t , sin х = t . A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0 Решаются методом введения новой переменной. 2.Однородные уравнения первой и второй степени. I степени . A sinx + B cosx = 0 : cosx A tg x + B = 0 II степени . A sin 2 x + B sinx cosx + A cos 2 x = 0 : cos 2 x A tg 2 x + B tgx + C = 0 Решаются методом разложения на множители и методом введения новой переменной . 3. Уравнение вида: А sinx + B cosx = C . А, В, С 0 Применимы все методы.
4. Понижение степени. А cos 2 x + В = C . A cos2x + B = C. Решаются методом разложения на множители. A sin2x + B = C. A sin2x + B = C. Сводятся к однородным уравнениям С = С( ).
Формулы . a cosx + b sinx заменим на C sin ( x + ), где sin = cos = — вспомогательный аргумент. Универсальная подстановка. х + 2 n ; Проверка обязательна! Понижение степени. = (1 + cos2x ) : 2 = (1 – cos 2x) : 2 Метод вспомогательного аргумента.
Сведение к однородному. sinx cosx + 6 cos 2 x = 5. Пример. 5 sin 2 x + Разложение на множители. Пример. — 2 cosx = 4 sinx — sin 2 x A sin2x + B sin 2 x = C, Asin2x + Bcos 2 x = C. Уравнения вида
1.Потеря корней: делим на g (х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g (х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения. Проблемы ,возникающие при решении тригонометрических уравнений
Уравнение . Уравнение . Поделив уравнение на , получим , , При решении этой задачи обе части уравнения были поделены на . Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения корнями данного уравнения. Если , то из уравнения следует, что . Однако и не могут одновременно равняться нулю, так как они связаны равенством . Следовательно, при делении уравнения , где , , на (или ) получаем уравнение, равносильное данному.
, x = y + . Решить уравнение cos²x + sinx cosx = 0 1) Делить на cosx нельзя, так как в условии не указано , что cosx не равен нулю. Но можно утверждать, что sinx не равен нулю, так как в противном случае cosx равен 0, что невозможно , так как sin²x-cos²x =1. Значит можно разделить на sin²x . 2) Решим уравнение разложением на множители: cos²x + sinx cosx = 0 , с osx ( cosx + sinx ) = 0 , с osx = 0 или cosx + sinx = 0, tg x=-1,
Уравнения, линейные относительно sin x и cos x а sin x + в cos x = с. Если а=в=0, а с не равно 0, то уравнение теряет смысл; Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество. Рассмотрим случаи, когда а , в , с не равны 0. Примеры: 3 sin 5x — 4 cos 5x = 2 2 sin 3x + 5 cos 3x = 8. Последнее уравнение не имеет решений, так как левая часть его не превосходит 7. Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tg х ; сведением уравнения к однородному; введением вспомогательного аргумента и другими. Решение этих уравнений существует при
Данное уравнение является уравнением вида , (1) где , , , которое можно решить другим способом. Разделим обе части этого уравнения на : . (2) Введем вспомогательный аргумент , такой, что . Такое число существует, так как . Таким образом, уравнение можно записать в виде . Последнее уравнение является простейшим тригонометрическим уравнением.
Уравнение . Используя формулы sin x = 2 sin cos , cos x = cos 2 — sin 2 и записывая правую часть уравнения в виде , получаем Поделив это уравнение на , получим равносильное уравнение Обозначая , получаем , откуда . 1) 2) Ответ: . 0 2 cos 2 cos 2 sin 4 2 sin 3 2 2 x x x x
4 sin ²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0
4 sin ²x — 4 sinx – 3 = 0 ( -1) n+1 П /6 + П n, n Z. 2 с os²x – sin x – 1 = 0 ± П /6 + П n ; -П /2+2 П n, n Z.
Решить уравнение Здесь Поделим обе части уравнения на 5: Введем вспомогательный аргумент , такой, что , . Исходное уравнение можно записать в виде , , откуда Ответ:
1 ctg x 1 tg x cos x sin x = 60 ° =45 ° =30 °
— 0 — 0 — ctg x 0 — 0 — 0 tg x 1 0 -1 0 1 cos x 0 -1 0 1 0 sin x =360 ° =270 ° =180 ° = 90 ° 0 ° А
Урок-повторение по теме «Тригонометрические уравнения и неравенства» (11-й класс)
Разделы: Математика
Класс: 11
Цели:
- Образовательные – систематизировать знания и создать разноуровневые условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
- Развивающие – способствовать формированию умений применять полученные знания в новой ситуации, развивать математическое мышление, речь.
- Воспитательные – содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.
Ход урока
- Оргмомент
- Математическая эстафета
- Конкурс капитанов
- Самостоятельная работа
- Угадай слово
- Подведение итогов. Домашнее задание
I. Оргмомент
Сегодня на уроке мы повторим тему «Тригонометрические уравнения и неравенства». Тем самым систематизируем знания и создадим разноуровневые условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений. Данная тема важна еще и тем, что тригонометрические уравнения встречаются в заданиях ЕГЭ во всех частях.
Рассадить учащихся по группам (их две), выбрать капитанов. Четырех учеников посадить за компьютеры для решения тестов. Одному ученику дать индивидуальное задание: решить уравнение, входящее в часть В тестов ЕГЭ.
II. Математическая эстафета (Приложение 3)
Данный этап позволит нам отработать все формулы тригонометрических уравнений.
Члены команды по очереди подходят к доске и решают очередное уравнение.
Задания для 1 команды (Приложение 2)
Задания для 2 команды
III. Конкурс капитанов
Пока капитаны у доски решают свои задания, проверим ученика с индивидуальным заданием: решить уравнение, входящее в часть В тестов ЕГЭ.
1 капитану решить уравнение (1 — cos2x)(tgx — √3) = 0
2 капитану решить уравнение (1 — 2sinx)(ctgx — 1) = 0
IV. Самостоятельная работа
Каждая группа получает карточку, в которой не только задания работы, но и карточка со вспомогательной консультацией по решению каждого задания.
Задание группе №1
1. Решите уравнение:
2. Решите неравенство:
3. Решите уравнение:
Группа №1
Консультация первого уровня.
1. а) Решите уравнение относительно cos х по общей формуле для корней квадратного уравнения, после чего получившееся уравнение решите относительно х.
б) Разложите левую часть уравнения на множители и примените условие равенства произведения нулю.
2. Запишите решение неравенства относительно аргумента “3х”, а дальше относительно “х”.
3. Решите систему способом подстановки.
4. Исследуйте знак выражения, стоящего под знаком модуля.
Консультация второго уровня.
1. а) Решите уравнение как квадратное относительно cos x, придете к совокупности уравнений cos x= -(1/2) и cos x= -1. Решая каждое из уравнений, учтите, что arсcos(-1/2) = 2π/3, а второе уравнение можно решать используя частный случай.
б) Имеем: sin x (sin x +√3cos x) = 0. Перейдем к совокупности уравнений sin x = 0; sin x+√3cos x= 0. Решаем как однородное уравнение I степени (деление обеих частей уравнения на cos x≠ 0 или на sin x≠ 0).
Консультации для дополнительных заданий второго уровня.
1. Заметим, что √3/2 = cos(π/6); 1/2 = sin(π/6). Имеем формулу sin(π/6 + x) в левой части уравнения. Решаем уравнение: sin(π/6 + x) = -(1/2)
2. Имеем: 2y 2 + y – 1 ≤ 0
Решаем графически на единичной окружности.
5 sin x — 6 cos x — 6 = 0
Вынесем общий множитель за скобки. Будем решать совокупность уравнений:
(имеем однородное уравнение I степени)
Задание группе № 2
1. Решите уравнение:
б) 2 sin 2 x + 5 sinx ∙ cosx — 7cos 2 x = 0.
2. Решите неравенство:
Дополнительно:
1. Решите уравнение:
2. Решите уравнение:
2 cos 2 x+ cos x — 1 ≤ 0.
3. Решите неравенство:
Группа №2
Консультация первого уровня.
1. а) Воспользуйтесь тождеством ctgx = 1/(tgx). Решается уравнение заменой переменной. При решении дробного уравнения вспомните алгоритм его решения.
б) Имеем однородное уравнение второй степени, решаем его деление обеих частей уравнения на cos x (или sin x). Затем сведем к решению квадратного уравнения.
2. Запишем решение неравенства для (π/2 + x), затем относительно “x”.
3. Решите систему способом подстановки, для этого из 1-го уравнения выразите одну переменную через другую и подставьте во второе уравнение. Решение тригонометрического уравнения записывается точками единичной окружности.
4. Помним, что верно равенство x 2 =│x│ 2 для любого x. Введите замену │sinx│= y. Решение сведется к решению квадратного (неполного) уравнения.
Консультация второго уровня.
1. а) Получив дробное уравнение y + (1/y) = 2. Умножив обе части уравнения на общий знаменатель y ≠ 0. Решаем квадратное уравнение y 2 — 2y+ 1 = 0. Проверьте корни уравнения. Сделайте обратную подстановку.
б) Введем новую переменную tg x= y, получаем 2y 2 + 5y— 7 = 0, решив его будем иметь tg x= 1, или tg x= -3,5. Решим каждое из уравнений.
Решаем
Решаем каждое из полученных уравнений относительно x.
Консультации для дополнительных заданий первого уровня.
1. Умножьте обе части уравнения на 1/2.
2. Введите замену: cos x = y и решите квадратное неравенство.
3. Воспользуйтесь формулами sin x = 2 sin(x/2)cos(x/2)
Консультации для дополнительных заданий второго уровня.
1. Заметим, что (√3/2)= cos(π/6); 1/2 = sin(π/6). Имеем формулу sin(π/6 + x) в левой части уравнения. Решаем уравнение: sin(π/6 + x) = -(1/2)
Решаем графически на единичной окружности.
5 sin x — 6 cos x — 6 = 0
Вынесем общий множитель за скобки. Будем решать совокупность уравнений:
(имеем однородное уравнение I степени)
Ответы для группы №1
Ответы к дополнительной части.
Ответы для группы №2
Ответы к дополнительной части.
В это время группа более сильных учащихся на доске должна решить следующее задание
Решите уравнение:
V. Угадай слово (Приложение 4)
И на последок еще такое задание, в котором всего одно слово, но какое?! Решив задания вы его и отгадаете. На доске находите карточку со своим ответом и переворачиваете ее.
V. Подведение итогов. Домашнее задание.
К работе прилагается тест в MS Excel (Приложение 5).
Как научить решать тригонометрические уравнения и неравенства: методика преподавания
Курс математики корпорации «Российский учебник», авторства Георгия Муравина и Ольги Муравиной, предусматривает постепенный переход к решению тригонометрических уравнений и неравенств в 10 классе, а также продолжение их изучения в 11 классе. Представляем вашему вниманию этапы перехода к теме с выдержками из учебника «Алгебра и начало математического анализа» (углубленный уровень).
1. Синус и косинус любого угла (пропедевтика к изучению тригонометрических уравнений)
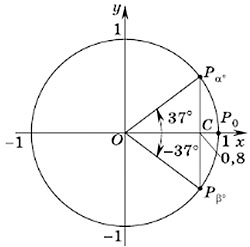
Пример задания. Найти приближенно углы, косинусы которых равны 0,8.
Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: Pα° и Pβ°, симметричных относительно оси абсцисс.
С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой Pα°:
α° ≈ 37° + 360°n, где n — любое целое число.
В силу симметрии относительно оси абсцисс точка Pβ° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:
β° ≈ –37° + 360°n, где n — любое целое число.
Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.
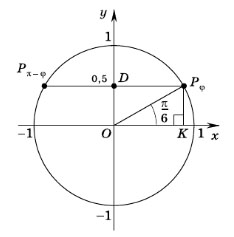
Пример задания. Найти углы, синусы которых равны 0,5.
Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).
Эта прямая пересекает единичную окружность в двух точках: Pφ и Pπ–φ, симметричных относительно оси ординат. В прямоугольном треугольнике OKPφ катет KPφ равен половине гипотенузы OPφ, значит,
Общий вид углов поворота с конечной точкой Pφ:
где n — любое целое число. Общий вид углов поворота с конечной точкой Pπ–φ:
где n — любое целое число.
Ответ: 
2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)
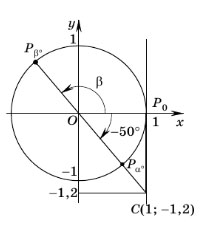
Пример 2. Найти общий вид углов, тангенс которых равен –1,2.
Пример задания. Найти общий вид углов, тангенс которых равен –1,2.
Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках Pα° и Pβ° — концах одного и того же диаметра. Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол Pα° OP0 равен –50°. Значит, общий вид углов, тангенс которых равен –1,2, следующий: –50° + 180°n (n — целое число)
По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,
Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.
http://urok.1sept.ru/articles/583786
http://rosuchebnik.ru/material/kak-nauchit-reshat-trigonometricheskie-uravneniya-i-neravenstva-metodi/