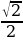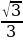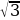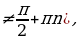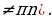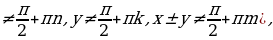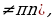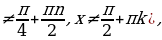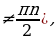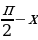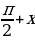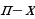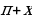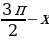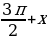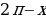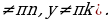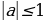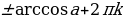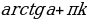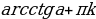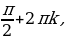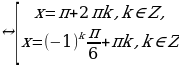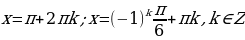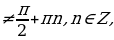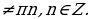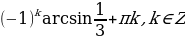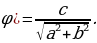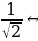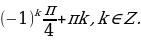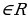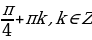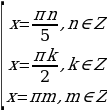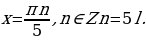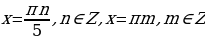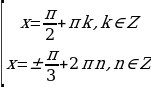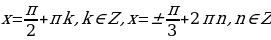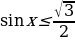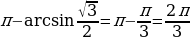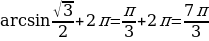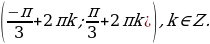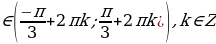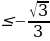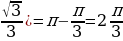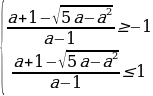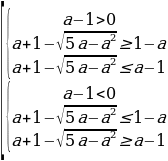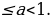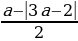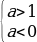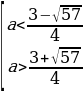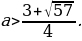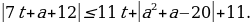Реферат по алгебре и началам анализа тригонометрические уравнения в школьном курсе алгебры
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 20»
РЕФЕРАТ ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
Ф. И.О. учащегося Клинцова Елизавета
Руководитель Козак Татьяна Ивановна,
учитель математики I категории
1.1 История тригонометрии как науки
1.2 Тригонометрия как учебный предмет
1.3 Тригонометрия в школе до 1966 года
1.4 Тригонометрия в школе после 1966 года
1.5 тригонометрия в современной школе
Тригонометрические уравнения в школьном курсе алгебры
2.1 Простейшие тригонометрические уравнения
2.2 Тригонометрические уравнения, сводящиеся к квадратным
2.3 Однородные уравнения
2.4 Уравнения, решаемые разложением на множители
2.5 Задачи на повторение
Тригонометрические уравнения на экзаменах
3.1 Специфика выпускного экзамена за курс средней полной школы
3.2 Тригонометрические уравнения на выпускном экзамене
3.2.1 Тригонометрические уравнения на обязательном уровне обучения
3.2.2 Тригонометрические уравнения из раздела 4
3.2.3 Тригонометрические уравнения повышенной сложности
Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, – что следуя этому методу, мы достигнем цели.
Тригонометрия, как и любая научная дисциплина, возникла из потребностей практической деятельности человека. Тригонометрия изучает важный класс функций – так называемых тригонометрических, а также их применение в геометрии. Само название «тригонометрия» греческого происхождения, обозначающие «измерение треугольника»: τρіγωνоν (тригонон) – треугольник, μετρειω (метрейн) – измерение, показывает что этот раздел математики связан с задачами решения треугольников, т. е. с задачами нахождения одних элементов треугольника по другим его известным элементам. Исторически тригонометрия и возникла из таких задач, но ими далеко не исчерпывается широкое применение тригонометрических функций в самых различных разделах математики, естествознания и техники.
В школьном курсе математики знакомство с тригонометрией начинается в 8 классе на уроках геометрии, когда вводится понятие синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника. Затем идёт расширение этого вопроса, и мы уже знакомимся с понятием синуса, косинуса, тангенса и котангенса произвольного угла. Рассматриваются теоремы синуса и косинуса, позволяющие решать треугольники.
На уроках алгебры в 9 классе помимо этих понятий мы рассматриваем ряд формул, позволяющих преобразовывать тригонометрические выражения; находить их значения; вычислять значения тригонометрических функций по заданному значению одной из функций и другие вопросы, связанные с тригонометрией.
В курсе алгебры и начала анализа в 10 классе начинается изучение темы «Решение тригонометрических уравнений и неравенств». На уроках мы рассмотрели приёмы решения тригонометрических уравнений и неравенств, но их оказалось немного. Я задумалась над тем, а есть ли другие приёмы решения тригонометрических уравнений. И выбирая в 11 классе экзамен по выбору, я решила исследовать этот вопрос и попытаться выяснить: что же предлагает (по типам) школьный курс алгебры и начал анализа, выпускной экзамен за курс средней полной школы.
Итак, цель моей работы:
¨ систематизировать, обобщить, расширить знания и умения, связанные с решением тригонометрических уравнений.
· повторить решение простейших тригонометрических уравнений;
· провести классификацию тригонометрических уравнений, предлагаемых в школьном курсе алгебры и начал анализа;
· рассмотреть тригонометрические уравнения, предлагаемые на выпускном экзамене.
¨ научный (изучение литературы);
1. История тригонометрии
1.1 История тригонометрии как науки
Зарождение тригонометрии относится к глубокой древности. Еще за долго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии. Постепенно в геометрии и астрономии установились понятия синуса, косинуса, тангенса угла.

Эти таблицы являются таблицами значений удвоенного синуса половины соответствующего центрального угла. В них были даны значения хорд для всех углов (через каждые пол градуса) от 0° до 180°. Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в самостоятельную науку» а считалась частью астрономии.
Важный вклад в развитие тригонометрии был внесен индийской математикой в период V-X1I в. н. э. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», что буквально означало “половина тетивы лука”. Индийцы составили таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 0° до 90° (через каждые 3°45′). Эти таблицы были точнее таблиц Птолемея.



В XV-XVII в. в Европе было составлено и издано несколько тригонометрических таблиц. Над их составлением работали крупнейшие ученые: Н. Коперник (), И. Кеплер (), Ф. Виет () и др. В России первые тригонометрические таблицы были изданы в 1703 г. при участии .
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (). Эйлер стал рассматривать значения тригонометрических функций как числа – величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи sin α, cos α, tg α, ctg α. Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого .
1.2 Тригонометрия как учебный предмет
Тригонометрия состоит их двух различных частей:
а) первой (ее обычно называют гониометрией) – части математического анализа, где независимо от геометрических соображений аналитически раскрывается учение о трансцендентных тригонометрических функциях с их свойствами;
б) второй – собственно тригонометрии, где соединяются математический анализ и геометрия того или иного пространства.
В XVIII в., и особенно в XIX в., в связи с бурным развитием дифференциального исчисления, возникает новый предмет – математический анализ, и тригонометрия становится его составной частью. А учебный предмет тригонометрия с его первоначальной геометрической основой продолжает существовать самостоятельно. То есть возникают два направления учебного предмета тригонометрии: аналитическое решение треугольников и изучение свойств круговых (тригонометрических) функций.
В 1848 г. академик предложил систему индуктивного изучения тригонометрии:
а) сначала (в младших классах) изучается тригонометрия острого угла как учение о вычислительных приемах решения треугольников и фигур, сводимых к ним;
б) затем (в старших классах) обобщаются понятия тригонометрии острого угла, то есть излагаются основы теории тригонометрических функций любого действительного аргумента.
С тех пор эта система успешно применялась в отечественной методике обучения тригонометрии в школе
1.3 Тригонометрия в школе до 1966 года
Основательное изучение тригонометрии начиналось очень рано, уже в 14 лет.
В Программе 1921 г. предписывалось во втором полугодии 7-го класса (2 часа в неделю) изучить раздел «Тригонометрия».
Изучение тригонометрического материала в семилетней школе было нацелено, прежде всего, на освоение практических методов решения определенных вычислительных геометрических задач, на расширение возможности вычисления элементов треугольников – на тригонометрию треугольника. При этом раннее введение тригонометрии треугольников существенно повышало требования к числовой культуре школьника и, прежде всего, требовало знания элементов теории приближений и измерений.
Несколько позже, уже в программе средней десятилетней школы (например, в программе 1949 г.), начало изучения тригонометрии перемещается в курс геометрии 8-го класса, а в 7-м классе, также в курсе геометрии, обращается особое внимание (в пояснительной записке замечено даже «в особенности в сельских школах») на необходимость проведения измерительных работ на местности: провешивание линий, промер линий, проведение перпендикуляров эккером, измерение углов, определение расстояний и высот. Тем самым, с одной стороны, серьезно усиливался прикладной характер изучаемого в массовой школе математического материала, а с другой – создавалась хорошая опора для изучения формального материала курса тригонометрии.
А вот в 9-м классе (десятилетней школы) данной программы тригонометрия начинает обретать черты отдельной школьной дисциплины. Внимание сосредотачивается на четырех тригонометрических функциях: синус, косинус, тангенс и котангенс. Секанс и косеканс даются в ознакомительном порядке. В 10-м классе предусматривается «решение косоугольных треугольников, основанное на теоремах синусов, косинусов и тангенсов с применением в соответствующих случаях различных таблиц».
Роль тригонометрического материала в школьном образовании оценивалась столь высоко, что до 1966 г. в 9-х и 10-х классах изучалась отдельная дисциплина «Тригонометрия», на которую выделяли 2 часа в неделю. Этот курс изучался параллельно с курсом алгебры. Для этой дисциплины был подготовлен и введен отдельный учебник ( «Тригонометрия. Учебник для 9-10 классов средней школы, выдержавший десять изданий).
Учебник тригонометрии предназначался для старшей ступени обучения, то есть для тех школьников, кто планировал поступать в высшие учебные заведения страны.
Тригонометрическим уравнениям уделялось совсем немного внимания. В учебнике рассматривались простейшие тригонометрические уравнения, способ приведения к одной функции, способ разложения на множители и иллюстрировались возможности потери решений и появления посторонних решений при выполнении преобразований. Вместе с тем выделялся целый параграф, посвященный приближенным решениям тригонометрических уравнений.
1.4 Тригонометрия в школе после 1966 года
Начиная с середины шестидесятых годов в ходе подготовки и осуществления реформы школьного математического образования, получившей в дальнейшем название «реформа «, отношение к тригонометрии стало меняться и со временем изменилось принципиально.
Прежде всего, это выразилось в изменении программных целей изучения данного раздела науки в школе. В программах основной школы семидесятых годов (например, в программе 1978 г. для десятилетней школы) о начале изучения такого специфического раздела математики, как тригонометрия, даже не упомянуто. Просто в пояснении к отдельным темам сказано, что в 8-м классе изучаются четыре темы, одна из которых «Поворот и тригонометрические функции».
Тригонометрия утратила свое значение как отдельная школьная дисциплина и стала просто одним из многих разделов курса математики, который надлежало осваивать в силу того простого факта, что вопросы тригонометрии «традиционно» присутствовали в школьных программах и учебниках.
Обучение проводилось по учебнику , . В поддержку этого учебника был издан сборник задач , , .
Но эти учебник и задачник переходного периода проработали в школе менее 10 лет. Вскоре им на смену пришел учебник «Алгебра и начала анализа. Учебное пособие для 9 и 10 классов средней школы» (1975) под редакцией . В нем тригонометрия изучалась в конце 9-го в начале 10-го классов. Формально содержание обучения в целом было сохранено и даже расширено. Здесь вводилось радианное измерение угловых величин, тригонометрические функции и их свойства, формулы сложения, производные и исследование тригонометрических функций, тригонометрические уравнения и неравенства. В дальнейшем, после перехода к одиннадцатилетней школе, тригонометрический материал в основной ступени был значительно усилен.
1.5 Тригонометрия в современной школе
К концу XX в. в примерных программах основного общего образования объем рекомендуемого к изучению в массовой школе тригонометрического материала заметно сократился. Например, в программе подготовленной в 1998 г. предлагается рассмотреть в основной школе:
1. в курсе алгебры — синус, косинус, тангенс и котангенс произвольного угла, основные тригонометрические тождества, формулы приведения;
2. в курсе геометрии — синус, косинус, тангенс и котангенс острого угла, решение прямоугольных треугольников, метрические соотношения между элементами произвольного треугольника: теорема синусов и теорема косинусов.
В старшей ступени обучения для общеобразовательных классов тригонометрические формулы сложения и их следствия, тождественные преобразования тригонометрических выражений получили статус необязательного материала. Оставлены лишь тригонометрические функции числового аргумента, свойства и графики тригонометрических функций. А более серьезные вопросы тригонометрии отнесены к программам повышенного уровня. Но и здесь преобразование суммы тригонометрических функций в произведение и произведения в сумму отнесено к необязательному материалу.
Таким образом, после 1966 г. тригонометрический материал стал постепенно «выжиматься» не только из основной школы, но и из курса старшей ступени обучения для общеобразовательных классов.
Введение всеобщего и обязательно десятилетнего образования в 1966 г. и последовавший затем переход к «знаниевой» педагогике принципиально изменили ситуацию, прежде всего в старшей и основной ступенях. Возникло две проблемы.
Во-первых, это проблема обучения всех детей в течение одиннадцати лет одному и тому же содержанию. Разные способности детей не дают возможности качественно решить эту проблему, если не признать необходимость принципиально понизить уровень среднего образования. Отсюда и все споры вокруг стандартов, и учебная перегрузка детей, и отвращение многих из них к математике как к наиболее формализованному учебному предмету. А тригонометрические функции действительного аргумента в курсе математики по части формализации занимают не последнее место. Отсюда и стремление исключить этот материал из обязательного минимума содержания образования.
Одновременно с этим тригонометрический материал традиционно популярен при проведении всевозможных конкурсов, олимпиад и при отборе математически одаренных учащихся, поскольку он чрезвычайно удобен для усложнения заданий.
Другими словами, тригонометрический материал, теряя свое общеобразовательное значение в представлениях некоторых специалистов в области методики обучения математике, на практике все больше обретает характер селективного инструмента. Соответственно возрастает потребность определенной части учащихся и их родителей в хорошей организации обучения этому разделу в школьный период обучения. По крайней мере, к этой части учащихся можно отнести тех, кто заинтересован в продолжении обучения в учреждениях среднего и высшего профессионального образования. А в настоящее время это не менее половины выпускников.
Таким образом, вторая проблема – подготовка в массовой школе одаренных в академическом смысле детей к поступлению и обучению в вузе.
До шестидесятых годов такие понятия как «репетитор», «факультатив», «класс (школа) с углубленным изучением предмета» и т. п. не были известны школьным работникам и их родителям. Действительно, поскольку только половина детей переходили на обучение в старшую ступень, а в ней допускалось отчисление за неуспеваемость, то необходимости понижать уровень образования в старшей ступени даже не возникало. В так организованной школе добравшийся до выпуска школьник в основном был весьма серьезно обучен и имел широкий кругозор.
В семидесятых-восьмидесятых годах стали возникать классы, а затем и школы с углубленным изучением какого-либо предмета, в девяностых – лицеи и гимназии.
В общеобразовательных классах, и в классах с углубленным изучением того или иного предмета или цикла предметов освоение опыта «создания» фрагмента науки, безусловно, должно присутствовать. А тригонометрия для этого, как и прежде, наиболее естественный раздел школьной математики.
2. Тригонометрические уравнения в школьном курсе алгебры
2.1 Простейшие тригонометрические уравнения
Уравнением называется равенство, содержащее переменную. А уравнения, в которых неизвестные содержатся под знаком тригонометрических функций, называются тригонометрическими уравнениями.
Решением уравнения с неизвестным х называют число хо, при подстановке которого в уравнение вместо х получается верное числовое равенство. Отличительная особенность тригонометрических уравнений – бесконечное множество корней. Эта особенность связана с характерным свойством тригонометрических функций – периодичностью. Решить уравнение – это значит найти все его решения или показать, что их нет.
Решение любого уравнения: сводится к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax2 + вx + c =0.
Необходимость классификации уравнений вызывается невозможностью найти общий метод их решения. Известно, что целые алгебраические уравнения со времен Декарта () классифицируются по степени уравнения. Чем выше степень таких уравнений, тем сложнее взаимная связь неизвестного с коэффициентами уравнения и тем труднее выразить это неизвестное через коэффициенты.
В тригонометрии предпринимались попытки создавать свою специфическую классификацию. Пример такой классификации, содержащей восемь типов тригонометрических уравнений, приводится в пособии , «Курс тригонометрии». Классифицировать тригонометрические уравнения по степени не имеет большого смысла, так как тригонометрические уравнения допускают повышение и понижение степени за счет использования формул половинного и двойного аргумента. Очевидно, что классифицировать тригонометрические уравнения имеет смысл с опорой на методы их решения. Здесь я попытаюсь показать, с какими методами решения тригонометрических уравнений мы сталкиваемся в учебнике для 10-11 классов общеобразовательных учреждений «Алгебра и начала анализа» под редакцией (2001 г.).
Решение тригонометрических уравнений выполняется в большинстве случаев (с помощью различных преобразований) путём сведения их к простейшим тригонометрическим уравнениям. Поэтому и работу с тригонометрическими уравнениями естественно начинать с простейших тригонометрических уравнений.
Уравнение f(x) = а, где а – данное число, а f(x) – одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением. В школьном курсе рассматриваются следующие простейшие тригонометрические уравнения: sin t = a, cos t = a, tg t = a, ctg t = a.
Рассмотрим, при каких значениях а простейшие тригонометрические уравнения разрешимы (имеют решения) и как правильно находить все решения таких уравнений.
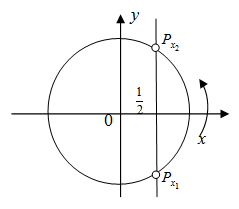
Так как множество значений функции у = sinx – отрезок [– 1; 1], то уравнение sin t = a разрешимо только в том случае, когда |а| ≤ 1. И тогда решение данного уравнения находится по формуле: t = (– 1)narcsin a + πn, где n Î Z. Соответственно, если |а| > 1, то уравнение не имеет действительных корней. Это обстоятельство следует хорошо помнить, т. к. забывая об этом, часто допускают ошибки. Например, при решении уравнения sin t = 



Если а = – 1; 0; 1, то рассматривают частные случаи решения данного уравнения.
Это уравнение имеет решения тогда и только тогда, когда |а| ≤ 1. Если это условие выполнено, то все решения уравнения cos t = a записываются в виде: t = ± arccos а + 2πn, где n Î Z. Соответственно, если |а| > 1, то уравнение не имеет действительных корней.
Если а = – 1; 0; 1, то также рассматривают частные случаи решения данного уравнения.
Данное уравнение имеет решения при любом значении а Î (– µ; µ). Все решения уравнения задаются формулой t = arctg а + πn, где n Î Z. Частные случаи здесь не рассматривают.
Данное уравнение имеет решения при любом значении а Î (– µ; µ). Все решения уравнения задаются формулой t = arсctg а + πn, где n Î Z. Частные случаи здесь также не рассматривают.
Ряд уравнений путём элементарных преобразований: перенос слагаемых из одной части уравнения в другую, деление обеих частей уравнения на одно и тоже число, отличное от нуля, также очень легко сводятся к простейшим.
При решении простейших тригонометрических уравнений вида Аsin(вх + с) = d, Аcos(вх + с) = d, Аtg(вх + с) = d, Аctg(вх + с) = d следует обратить внимание на то, что они приводятся к виду sin(вх + с) = а, cos(вх + с) = а, tg(вх + с) = а, ctg(вх + с) = а.
Сведение тригонометрических уравнений к простейшим тригонометрическим уравнениям выполняется различными способами. Первоначально надо рассмотреть тригонометрические уравнения, в которых под знаком тригонометрических функций стоит более сложное выражение, зависящее от х. для решения таких уравнений можно обозначить выражение, стоящее под знаком тригонометрической функции, одной буквой; решить простейшее тригонометрическое уравнение, а потом найти х, решая алгебраическое уравнение.
К таким уравнениям относятся уравнения:
№ 000, 139, 142(а, в), 143(а), 144(а), 145(б, г), 146(б), 173(в)
№ 000, 137, 142(б, г), 143(б), 144(в), 145(а), 146(г), 172(б)
№ 000(а, в, г), 141(а, в), 143(г), 144(б), 145(в), 146(в), 173(б)
№ 000(б), 141(б, г), 143(б), 144(г)
Покажу на примерах, как решаются такие уравнения с применением выше указанных формул.
х = (– 1)n + 1 
Ответ: х = (– 1)n + 1 
= 
х = 
Ответ: х = 



Проблема решения тригонометрических уравнений состоит не в большом количестве разнообразных формул, а в выборе направления, по которому необходимо двигаться для решения уравнения. Первый шаг на пути решения тригонометрического уравнения – это попытка отнести его к какому-либо типу, и если это удаётся, то применить характерный для данного типа уравнения приём. Рассмотрим основные типы уравнений, предлагаемых в школьном учебнике под редакцией . В учебном пособии приёмы решения тригонометрических уравнений не конкретизируются, а рассматриваются на нескольких конкретных примерах.
Для решения тригонометрических уравнений чаще всего используется два метода: введения новой переменной и разложения на множители.
Одним из самых общих методов решения тригонометрических уравнений является сведение тригонометрического уравнения к алгебраическому относительно одной тригонометрической функции с использованием тригонометрических формул: cos2х = 1 – sin2х, sin2х = 1 – cos2х,
Уравнения вида sin ах ± sin вх = 0, cos ах ± cos вх = 0 решаются заменой суммы (разности) синусов и косинусов произведением.
Часто, особенно при решении квадратного уравнения относительно одной из тригонометрических функций, используется метод введения новой переменной.
2.2 Тригонометрические уравнения, сводящиеся к квадратным
Сведение тригонометрического уравнения к алгебраическому относительно одной тригонометрической функции – один из самых общих методов решения тригонометрических уравнений. В этом разделе рассмотрим уравнения, которые после введения нового неизвестного t = f(x), где f(x) – одна из основных тригонометрических функций, превращаются в квадратные. К таким уравнениям можно отнести уравнения вида: asin2x + вsin x + c = 0, аcos2x + вsin x + c = 0 и т. д. Но в большинстве случаев приходится исходное уравнение преобразовать так, чтобы оно приобрело нужный вид. Для этого чаще всего используется основное тригонометрическое тождество sin2х + cos2х = 1.
В учебнике это: № 000, 165, 166, 167, 168(б, г), 171(б, г).
Покажу на примерах, как решаются такие уравнения.
Введём новую переменную: t = sin х. Тогда данное уравнение можно записать в виде: 2t2 + t – 1 = 0. это квадратное уравнение. Его корни: t1 = – 1; t2 = . Тогда sin х = –1 и sin х = – . Решим каждое из получившихся простейших уравнений.
1) sin х = –1 (это частный случай),
Курсовая работа по теме тригонометрические уравнения и неравенства с параметром
Просмотр содержимого документа
«Курсовая работа по теме тригонометрические уравнения и неравенства с параметром»
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
«Ульяновский государственный педагогический
университет имени И.Н. Ульянова»
(ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»)
Кафедра методик математического и информационно-технологического образования
Решение тригонометрических уравнений и неравенств с параметрами.
студентки 3 курса группы МИЯ-15
Специальность / Направление подготовки 44.03.05 Педагогическое образование
Специализация / Профиль Математика/ Иностранный язык
Заключновой Ирины Сергеевны
Научный руководитель к.п.н., доцент Кузина Н.Г.
(оценка цифрой и прописью) (подпись науч. рук-ля / расшифровка подписи)
(количество баллов) (дата)
(дата) (журнал регистрации)
Глава 1. Теоретические основы решения тригонометрических уравнений и неравенств с параметром 4
1.1 Исторические сведения о развитии тригонометрии 4
1.2 Тождественные преобразования тригонометрических выражений 5
1.4 Методы решения тригонометрических уравнений с параметром 10
1.4 Решение тригонометрических неравенств с параметром 16
Выводы по первой главе 21
Глава 2. Практикум по решению тригонометрических уравнений и неравенств с параметром 22
2.1 Решение тригонометрических уравнений с параметром 22
2.2 Решение тригонометрических неравенств с параметром 28
Выводы по второй главе 33
Список используемых источников 36
Данная работа посвящена исследованиям, лежащим в области математики, и касается тригонометрического раздела математики. Актуальность данной темы состоит в том, что тригонометрические уравнения одна из самых сложных тем в школьном курсе. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий ЕГЭ для 11 класса. А тригонометрические уравнения и неравенства с параметрами – наиболее сложные, но зато и самые интересные. Именно задачи такого типа развивают сообразительность, смекалку, догадливость, находчивость в учениках. Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях имеют конечное число корней, а в тригонометрических — бесконечное, что сильно усложняет отбор корней и выбор значения параметра.
Цель курсовой работы заключается в овладении методами решения основных типов тригонометрических уравнений и неравенств с параметрами.
Для осуществления обозначенной цели служат следующие задачи:
Отобрать теоретические сведения необходимые для решения тригонометрических уравнений и неравенств с параметрами
Сформировать понимание у учащихся работы с тригонометрическими задачами с параметрами
Выделить основные типы тригонометрических уравнений с параметрами и методы их решения на основе рассмотрения примеров
Овладеть методами решения основных типов тригонометрических уравнений и неравенств с параметрами
Изучить различные подходы и методы решений тригонометрических уравнений и неравенств с параметрами
Объект исследования – тригонометрические уравнения и неравенства с параметром. Предмет исследования – методы решения тригонометрических уравнений и неравенств с параметром.
При написании курсовой работы были использованы методы исследования: теоретические (анализ, классификация, индукция, обобщение) и практические (сравнение, материальное моделирование).
Методологической основой для исследования послужили научные труды известных математиков. В качестве теоретической базы исследования были использованы научные статьи, учебники по математике: Гусятников Н.В., Гусятников В.В.; Коноплева О.А. Практической базой исследования послужили сборники задач: Евдокимова Н.Н.; Мордкович А.Г., Литвиненко В.Н.
Глава 1. Теоретические основы решения тригонометрических уравнений и неравенств с параметром
- тригонометрические уравнения и неравенства встречаются в курсе алгебры и начала анализа, в разделе ЕГЭ по математике
- тригонометрия встречается в таких науках, как физика, биологии
- не последнюю роль играют и в медицине, и, что самое интересное, без них не обошлось даже в музыке и архитектуре.
- узнать как можно больше применений науки тригонометрия в повседневной практике
- изучить способы решения тригонометрических уравнений и способы выбора корней, принадлежащих промежутку
- расширить знания о применении тригонометрических уравнений в разных сферах жизни человека
- познакомиться с историей возникновения тригонометрических уравнений
- научиться решать тригонометрические уравнения
- уметь выбирать корни уравнения, принадлежащие промежутку
- сделать подборку задач из ЕГЭ
- поработать в Microsoft Word, Microsoft PowerPoint
- получить опыт публичного выступления
- ресурсы Интернет – сайтов, содержащих тригонометрические уравнения
- изучила материал энциклопедий и справочников
- просмотрела и выбрала задания из Демо — вариантов ЕГЭ разных лет по математике
- изучила способы решения тригонометрических уравнений и выбор корней уравнения принадлежащих отрезку
- поиск информации в источниках, справочниках
- работа с ресурсами Internet
- обработка и анализ информации
- умение работать в Microsoft PowerPoint и Microsoft Word
- человек не сможет обойтись в жизни без тригонометрических уравнений
- тригонометрические уравнения не нужны человеку в жизни.
- я считаю, что в XXI веке все научные работы требующие исследования базируются на тригонометрических функциях, уравнениях. По этому знания о тригонометрических уравнениях нужны каждому. Решение тригонометрических уравнений встречается в ЕГЭ по математике
- не только рассмотрела все способы выбора корней тригонометрического уравнения принадлежащего отрезку, но и ликвидировала свои проблемы по данной теме. Для меня это очень важно при сдаче ЕГЭ по математике
- выяснила какое значение имеют тригонометрические уравнения в жизни человека и как они работают в стране
- доказала, что в современном мире прожить без знаний тригонометрический уравнений невозможно. Чтобы быть хорошим специалистом, уметь разбираться в большом потоке информации, необходимо знать тригонометрические уравнения.
- изучение столь важной и интересной темы дает положительную мотивацию для самообразования.
- Ведём замену а.
- Находим корни квадратного уравнения.
- Возвращаемся к замене и решаем простейшее тригонометрическое уравнение.
- Записываем ответ.
- Разделим обе части уравнения на cos 2 x ≠ 0.
- Ведём замену а.
- Находим корни квадратного уравнения.
- Возвращаемся к замене и решаем простейшее тригонометрическое уравнение.
- Записываем ответ.
- Если a 2 +b 2 2 , то уравнение (1) не имеет решений, так как уравнение (2) не имеет действительных корней.
- Если a 2 +b 2 ≥с 2 и с≠-b, то из уравнения(3) найдем: x=2arctg ((a±√( a 2 +b 2 -с 2 )/(b+c))+2nπ, nϵZ.
- Если с=-b, то уравнение (1) имеет два множества решений: x=(2n+1)π и x=-2 arctg++2nπ, nϵZ.
- Запишем уравнение в виде: 2a sin(x/2) cos(x/2)+ b(cos 2 (x/2)- sin 2 (x/2))= c(cos 2 (x/2)+ sin 2 (x/2)), т.е. однородное уравнение:(с+b) sin 2 (x/2)- 2a sin(x/2) cos(x/2)+(c-b) cos 2 (x/2)=0 и т.
- Практическое применение тригонометрии
- Исторические сведения о развитии тригонометрии
Слово «тригонометрия» составлено из двух греческих слов: «тригонон» — треугольник и «метрео» — измеряю. Основной задачей тригонометрии является нахождение неизвестных параметров треугольника по данным значениям других его параметров.
Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы, позволявшие отыскивать хорду окружности по стягиваемой ею дуге. Дуги измерялись в градусах и минутах.
Все древние цивилизации вносили свой клад в дело накопления тригонометрических знаний. На одной из глиняных табличек Древнего Вавилова, возраст которой определяется вторым тысячелетием до нашей эры, решается тригонометрическая задача.
Значительно развили тригонометрию индийские средневековые астрономы и арабские ученые. В X веке багдадский ученый Абу-ль-Вефа присоединил к понятиям синусов и косинусов понятия тангенсов, котангенсов, секансов и косекансов. Абу-ль-Вефа установил также основные соотношения между ними. Благодаря работам знаменитого арабского ученого Насир эд-Дина (1201-1274) тригонометрия становится самостоятельной научной дисциплиной. Насир эд-Дин рассмотрел все случаи решения плоских и сферических треугольников. В XII веке с арабского языка на латинский был переведен ряд астрономических работ, по которым европейцы познакомились с тригонометрией, не многие работы Насир эд-Дина остались им неизвестны.
Выдающийся немецкий астроном XV века Региомонтан (1436-1476) заново сформулировал теоремы Насир эд-Дина. Региомонтан составил таблицы синусов плоских углов с точностью до седьмой значащей цифры. В середине XVIII века, благодаря русскому академику Леонарду Эйлеру (1707-1783), тригонометрия приняла современный вид. Он разработал её как науку о тригонометрических функциях, ввел записи 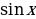
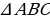
Эйлер рассматривал тригонометрические функции аргумента х – радианной меры соответствующего угла, давая этому аргументу различные значения: положительные, отрицательные и даже комплексные. Он же ввел и обратные тригонометрические функции.
- Тождественные преобразования тригонометрических выражений
Напомним основные факты тригонометрии.
Знаки тригонометрических функций по четвертям:
Некоторые значения тригонометрических функций
Функция y=cos x является четной, остальные тригонометрические функции нечетные:
tg(-x)=-tg x ( x
ctg(-x)=-ctg x (x
Все тригонометрические функции являются периодическими. При этом Т=2 

sin(x+2 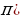

cos(x+2 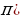

tg(x+ 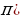

ctg(x+ 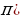

Формулы сложения аргументов:
sin(x 

cos(x 
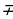
tg(x 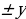
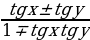
ctg(x 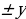
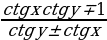
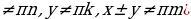
Формулы, связывающие тригонометрические функции одного и того же аргумента:
tg x = 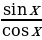
ctg x = 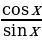
1+ tg 2 x = 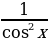
1+ ctg 2 x = 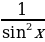
Формулы, связывающие тригонометрические функции аргументов, из которых один вдвое больше другого:
sin 2x = 2 sin x cos x,
tg 2x = 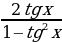
ctg 2x = 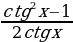
1 

Для облегчения запоминания указанных в таблице формул приведения можно применять следующее мнемоническое правило:
1) если дуга х откладывается от горизонтального диаметра ( 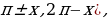
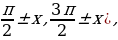
2) перед полученной функцией ставят тот знак, который имела бы выводимая функция в случае, если 0 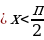
Формулы преобразования суммы тригонометрических функций в произведение:
sin x + sin y = 2 sin 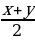
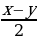
sin x — sin y = 2 sin 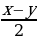
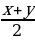
cos x + cos y = 2 cos 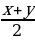
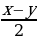
cos x — cos y = 2 sin 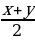
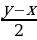
tg x 
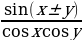
ctg x 
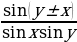
Формулы преобразования произведения тригонометрических функций в сумму:
sin x cos y = 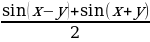
cos x cos y = 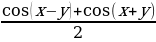
sin x sin y = 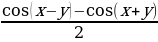
Имеется несколько определений параметра:
Параметр – это величина, входящая в формулы и выражения, значение которой является постоянным в пределах рассматриваемой задачи, но в другой задаче меняет свои значения.
Переменные a, b, c, …, k, которые при решении уравнения или неравенства считаются постоянными, называются параметрами, а само уравнение (неравенство) называется уравнением (неравенством), содержащим параметры.
Для решения квадратных уравнений с параметром необходимо находить контрольные значения параметра. Контрольные значения параметра – те значения, при которых обращается в 0:
— старший коэффициент в уравнении или в неравенстве;
— знаменатели в дроби;
— дискриминант квадратного двучлена.
1.4 Методы решения тригонометрических уравнений с параметром
Решить уравнение f (х; а) = 0 с параметром а – это значит, для каждого действительного значения а найти значения х, удовлетворяющих уравнению, или установить, что таких нет.
При решении тригонометрических уравнений с параметром наряду с единичной окружностью можно пользоваться координатной прямой для параметра. По мере решения уравнения на прямой появляются точки, разбивающие прямую на части, над каждой из которых записываем множество корней уравнения. Если координатная прямая заполнена, то это свидетельствует о том, что решение закончено и можно записывать ответ. При решении уравнений с параметрами нам будут необходимы знания о решении тригонометрических уравнения без параметра, поэтому рассмотрим далее методы их решения.
Напомним общие формулы решений простейших тригонометрических уравнений (если не сделано оговорок, то предполагается, что параметры n, k, l, m, … принимают любые целые значения).
sin x = a, где
x = (-1) k arcsin a +
сos x = a, где
x =
x =
x =
Отметим особо некоторые частные случаи простейших тригонометрических уравнений, когда решение может быть записано без применения общих формул:
sin x = 0 
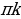
sin x = 1 
sin x = -1 
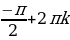
cos x = 0 
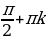
cos x = 1 
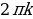
cos x = -1 
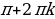
Проверка найденных решений необходима:
Если в процессе решения произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, приведение подобных членов),
Если в процессе решения уравнения использовалось возведение обеих частей уравнения в одну и ту же четную степень,
Если при решении применялись тригонометрические тождества, левая и правая части которых имеют неодинаковые области определения.
Основными методами, используемыми при решении тригонометрических уравнений, являются следующие методы: разложение на множители, сведение к квадратным уравнениям, решение однородных уравнений, универсальная подстановка, с помощью замены неизвестного, применение формул понижения степени, с применением формул тройного аргумента.
Решение тригонометрических уравнений разложением на множители. Метод разложения на множители заключается в следующем: если f(x)=f1(x) f2(x) … fn(x), то всякое решение уравнения f(x)=0 является решением совокупности уравнений f1(x)=0, f2(x)=0, … , fn(x)=0.
Обратное утверждение, неверно: не всякое решение совокупности уравнений является решением уравнения. Это объясняется тем, что решения отдельных уравнений могут не входить в область определения функции f(x). Поэтому, если при решении тригонометрического уравнения методом разложения на множители, функции, входящие в уравнение, определены не для всех значений аргумента, после нахождения решения должна быть сделана проверка, чтобы исключить лишние корни. можно поступать другим способом: находить область допустимых значений исходного уравнения и выбирать только те корни, которые входят в найденную область допустимых значений.
Пример №1. Решите уравнение: (2sin x – cos x)(1+ cos x)=sin 2 x
(2sin x – cos x)(1+ cos x)=1 – cos 2 x;
(2sin x – cos x)(1+ cos x)= (1- cos x) (1+ cos x);
(2sin x – cos x)(1+ cos x)- (1- cos x) (1+ cos x) ;
(1+ cos x)( 2sin x – cos x-1+ cos x)=0 
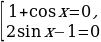

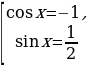
Ответ:
Решение тригонометрических уравнений, сводящихся к квадратным. При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества:
sin 2 x + cos 2 x=1,
tg 2 x + 1= 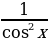
ctg 2 x + 1= 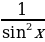
Пример №2. Решите уравнение: 6cos 2 x +5sinx – 7 = 0
6(1-sin 2 x) +5sinx – 7 = 0;
6sin 2 x -5sinx +1 = 0;
Введем подстановку y=sin x, тогда получаем квадратное уравнение
6y 2 – 5y +1 = 0. Находим корн у1 = 
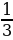

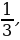
Ответ: x = 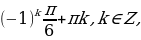
Решение однородных уравнений. Уравнение вида
b0sin n ax + b1sin n-1 ax cos ax + b2sin n-2 ax cos 2 ax + … +
+ b0n-1 sin ax cos n -1 ax + bncos n ax = 0, где b0, b1, … , bn — действительные числа, называются однородными уравнениями степени n относительно функций sin ax, cos ax. Общий подход к решению однородных уравнений основан на том, что корни уравнений sin ax = 0 или cos ax = 0 не являются корнями уравнения, так как, если, например cos ax = 0, то из уравнения следует, что и sin ax = 0, что противоречит основному тригонометрическому тождеству cos 2 x + sin 2 x =1. Следовательно, левую и правую части уравнения можно разделить на cos n ax и ввести подстановку y=tg ax, или разделить на sin n ax и ввести подстановку y=ctg ax.
Пример №3. Решите уравнение: sin x – 2cos x = 0
Уравнение является однородным уравнением первой степени. Разделим на cos x, получаем равносильное уравнение tg x = 2.
Ответ: x=arctg2 +
Решение уравнений с помощью введения вспомогательного аргумента. Рассмотрим уравнение asin x + bcos x = c, a 2 +b 2 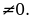
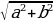
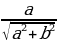
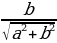
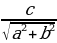
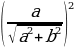
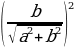
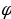
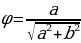
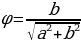
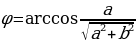
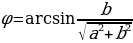
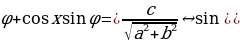
Пример №4. Решите уравнение: sin x + cos x = 1
Разделим левую и правую часть уравнения на 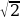
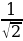
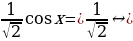
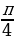
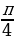

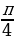
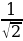

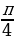
Ответ: x= — 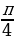
Решение уравнений методом универсальной подстановки. Тригонометрическое уравнение вида R (sin kx, cos nx, tg mx, ctg lx)=0, где R – рациональная функция, k, l, m, n 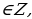
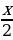
sin x = 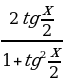
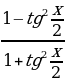
tg x = 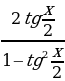
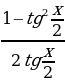
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку tg 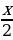
Пример №5. Решите уравнение:sin x + tg 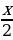
По условию задачи х 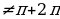
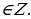
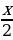
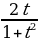
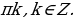
Ответ: x =2 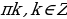
Решение тригонометрических уравнений с помощью замены неизвестного. Уравнение вида P (sin x 




Пример №6. Решите уравнение: 2(sin x + cos x) + sin 2x +1 = 0, x
2(sin x + cos x) + 2 sin x cos x +1 = 0;
Пусть sin x + cos x = y, (sin x + cos x) 2 = y 2 , 1+ 2 sin x cos x = y 2 ,
2 sin x cos x = y 2 -1, получим y 2 +2y-1+1 =0 ; y 2 + 2y=0; y(y+2)=0
y=0: sin x + cos x = 0, разделим на cos x 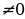
x = —
y= — 2: sin x + cos x = — 2, 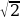
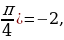
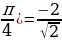
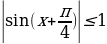
Ответ: x = —
Решение уравнения с применением формул понижения степен. При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени:
sin 2 x = 
cos 2 x = 
Пример №7. Решите уравнение: sin 2 x + sin 2 2x – sin 2 3x – sin 2 4x = 0. Применив формулу понижения степени, получим
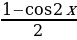
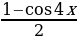
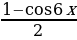
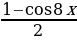
-2 sin 3x sin 5x -2 sin x sin 5x = 0,
2 sin 5x (sin 3x + sinx) = 0, 4sin 5x sin 2x sin x = 0. Последнее уравнение равносильно совокупности трех уравнений:
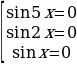
Решение из множества 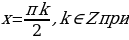
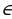
Ответ:
Решение уравнений с применением формул тройного аргумента. При решении ряда уравнений наряду с другими существенную роль играют формулы
sin 3x = 3sin x – 4sin 3 x,
cos 3x = 4 cos 3 x – 3cos x.
Пример №8. Решите уравнение: cos 3x = — 2cos x
Применив формулу, получим cos x ( 4cos 2 x – 1) = 0
cos x ( cos 2x + 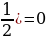
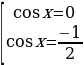
Ответ:
- Решение тригонометрических неравенств с параметром
Решение тригонометрических неравенств сводится, как правило, к решению простейших тригонометрических неравенств, т.е. неравенств вида sinx a, cos x a и т.д., также к решению совокупностей, систем или совокупностей систем простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенство для решения простейших тригонометрических неравенств во многих случаях удобно пользоваться геометрическим методом или с помощью окружности, на которой множество значений переменной, удовлетворяющих заданному простейшему неравенству, изображается в виде одной или нескольких дуг.
Аналогично тому, как с помощью неравенств задаются промежутки на числовой прямой, можно записывать и множество точек, принадлежащих той или иной дуге окружности 
Разберем случаи простейших уравнений для некоторых тригонометрических функций.
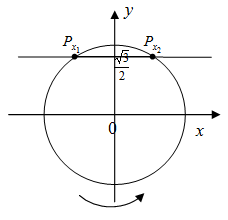
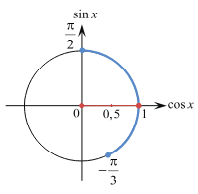
Пример №9. Решите неравенство:
Первый способ: Решим это неравенство графически. Для этого построим в одной системе координат график синуса y= 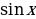
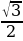
Выделим промежутки, на которых синусоида расположена ниже графика прямой y= 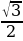
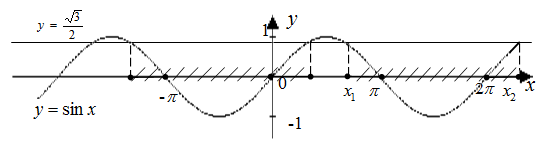
(рис. 1)
х1 =
х2 =
Получили интервал 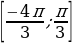

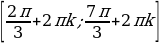
Второй способ: Построим единичную окружность и прямую y= 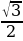
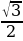
х1 =
х2 =
Учитывая периодичность функции синус, окончательно получим интервалы 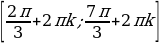
Ответ: х 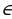
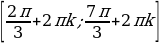
Пример №10. Решите неравенство: cos x
Построим единичную окружность и прямую x= 

x1=-arccos 
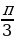

Учитывая периодичность косинуса, окончательно получим интервалы
Ответ: х
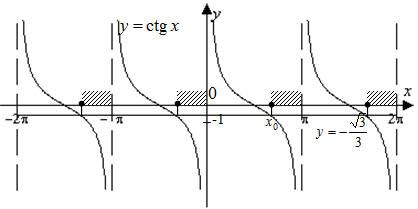
Пример №11. Решите неравенство: ctg x
Построим в одной системе координат графики функций: y=ctg x, y= 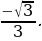
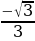
Найдем абсциссу точки x0, которая является концом одного из промежутков, на котором неравенство
x0=arcctg( 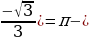
Другим концом этого промежутка есть точка 
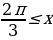


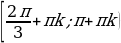
Ответ: х 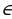
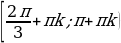
Если неравенство f(x; р) , ,
Решить неравенство с параметром — значит найти все значения параметров, при которых данные для решения тригонометрические неравенства будут иметь решение.
Выводы по первой главе
В первой главе были рассмотрены исторические сведения о развитии тригонометрии, тождественные преобразования тригонометрических выражений, которые необходимо знать для решения уравнений и неравенств. Определено, что такое параметр и его контрольные значения. При решении уравнений с параметрами нам будут необходимы знания о решении тригонометрических уравнения без параметра, поэтому были рассмотрены простейшие тригонометрические уравнения и восемь методов их решения, записаны решения для частных случаев простейших уравнений. Каждый метод был проиллюстрирован примером. Так же были рассмотрены методы решения тригонометрических неравенств, и разобраны случаи простейших уравнений для некоторых тригонометрических функций. Чтобы разобрать оба метода решения неравенств (геометрический и с помощью окружности) один из примеров решен двумя способами.
Глава 2. Практикум по решению тригонометрических уравнений и неравенств с параметром 2.1 Решение тригонометрических уравнений с параметром
Пример№1: Найдите все значения параметра а, при каждом из которых уравнение cos 4 x – (a + 2)cox 2 x – (a + 3) = 0 имеет решение.
Введем новую переменную: t =cos 2 x, t 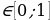
t1,2 = 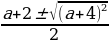
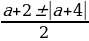
t1 = 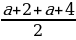
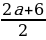
t2 = 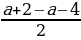
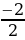
Число -1 не принадлежит промежутку 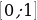
0 ≤ а +3 ≤ 1,
-3 ≤ а ≤ -2.
Ответ. Уравнение cos 4 x – (a + 2) cos 2 x – (a + 3) = 0 имеет решение при
a 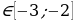
Пример№2: Найдите все значения параметра р, при которых уравнение
6sin 3 x = p – 10cos 2x не имеет корней.
6sin 3 x = p – 10cos 2x;
6sin 3 x + 10cos 2x = p;
6sin 3 x + 10(1 – 2sin 2 x) = p;
6sin 3 x – 20sin 2 x + 10 = p.
Введем новую переменную: t = sin x, t 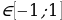
у = 6t 3 – 20t 2 + 10 и исследуем ее на наибольшее и наименьшее значения на отрезке 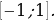

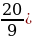
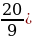
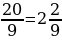
Число 2 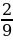
у(0) = 0 – 0 + 10 = 10,
у(-1) = -6 – 20 + 10 = -16,
у(1) = 6 – 20 + 10 = -4.
ymax (t) = 10, ymin (t) = -16 на отрезке 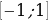
p 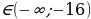
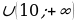
Ответ. Уравнение 6sin 3 x = p – 10cos2x не имеет корней при
p 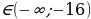
Пример№3: Решите уравнение sin 4 x + cos 4 x = a
Применяя формулы понижения степени получим:
( 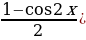
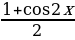
Найдем контрольные значения параметра. В данном случае это такие значения параметра, при которых правая часть уравнения 0 или 1
(если 2а – 1 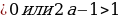
2а – 1 =0, то а = 
cos 4x = 4a -3в каждом из пяти случаев: 1) а 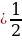

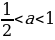
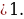
1) Если а 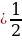

2) Если а = 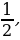
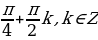
3) Если 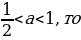
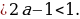
cos 2 2x = 2a – a к виду: 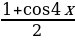
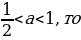
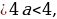
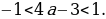
4х = 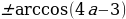
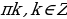
х = 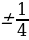
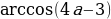
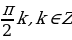
4) Если а=1, то уравнение cos 2 2x = 2a – a принимает вид cos 2 2x =1. Из этого уравнения находим х = 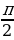
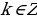
5) Если а 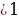
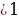
Затем, что если а = 
х = 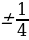
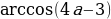
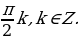
Ответ: 1) Если а 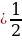
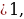
2) Если 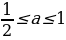
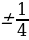
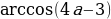
Пример№4:Решим уравнение (а-1)sin 2 x – 2(a+1)sin x +2a – 1=0.
Положим y=sin x, тогда данное уравнение примет вид
(a-1)y 2 – 2 (a+1)y + 2a-1=0. Первым контрольным значением параметра а будет значение а=1, которое обращает в нуль коэффициент при у 2 . При а=1 уравнение (a-1)y 2 – 2 (a+1)y + 2a-1=0 принимает вид -4у + 1 =0, откуда находим у= 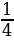
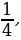
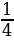
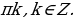
(a-1)y 2 – 2 (a+1)y + 2a-1=0. Имеем: 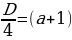
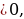

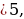
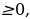
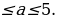
(a-1)y 2 – 2 (a+1)y + 2a-1=0 в каждом из следующих случаев: а 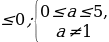
а 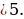
Если а 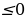
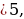
В случае 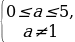
у1,2 = 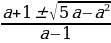
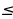
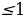
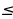
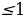
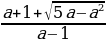
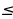
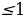
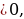
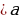
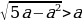
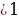
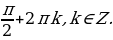
( из рассматриваемого множества системы 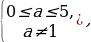
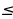
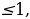
Система в свою очередь, равносильна следующей совокупности систем неравенств:
Решим первую систему из данной совокупности. Имеем:
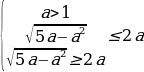
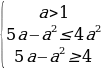
Откуда находим 1 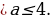
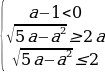
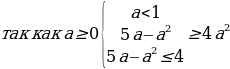
Итак, совокупность систем, а следовательно, и система имеют решения: 0 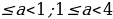
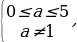
sin x = 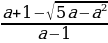
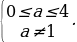
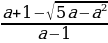
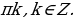
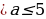
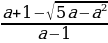
(а-1)sin 2 x – 2(a+1)sin x +2a – 1=0 не имеют корней.
Ответ: 1) если а=1, то х = (-1) k 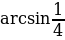
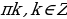
2) если 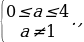
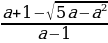
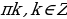
3) если а 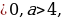
Пример№5: При каких значениях параметра а графики функций
y = sin 2 x + acos x и y = 3a – 2a 2 не имеют общих точек?
Другими словами, нужно найти такие значения параметра а, при которых уравнение sin 2 x + acos x = 3a – 2a 2 не имеет корней.
1 – cos 2 x + acos x + 2a 2 – 3a = 0;
cos 2 x – acos x – (2a 2 – 3a + 1) = 0.
Введем новую переменную: t = cos x, t 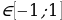
D = a 2 + 4(2a 2 – 3a + 1) = a 2 + 8a 2 – 12a + 4 = 9a 2 – 12a + 4 = (3a – 2) 2 ,
t1,2 = 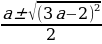
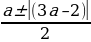
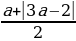
Так как 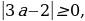
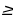
Случай 1. t1 
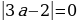
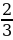
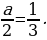
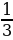
Случай 2. t1 
t2 1 1. Рассмотрим каждое из этих условий.
Условие 1. t1 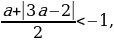
а + 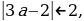
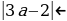
2 + а 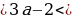
4 + а 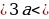
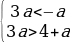
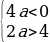
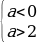
Система решений не имеет, значит, не существует таких значений а, при которых выполняется условие t1
Условие 2. t2 1.
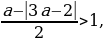
а — 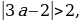
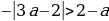
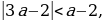
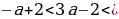
— а + 4 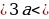
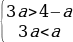
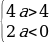
Система решений не имеет, следовательно, не существует таких значений а, при которых выполняется условие t2 1.
Условие 3. t2 1 1.
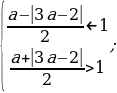
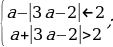
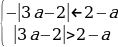
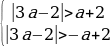
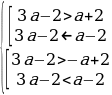
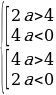
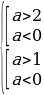
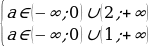
Таким образом, 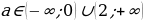
Ответ: Графики функций y = sin 2 x + acos x и y = 3a – 2a 2 не имеют общих точек, если 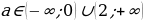
2.2 Решение тригонометрических неравенств с параметром
Пример№6: Найдите все значения параметра а, при каждом из которых множество решений неравенства 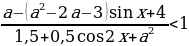
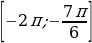
Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству 
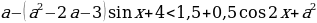
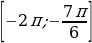
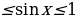
Пусть sin x = t, тогда cos 2x =1-2t 2 и неравенство принимает вид
a – (a 2 – 2a -3)t + 4 
t 2 – (a 2 – 2a -3)t – a 2 + a + 2 
Введем функцию f(t) = t 2 – (a 2 – 2a -3)t – a 2 + a + 2
(рис. 5)
Для того, чтобы множество решений неравенства
t 2 – (a 2 – 2a -3)t – a 2 + a + 2 


(рис. 6)
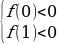

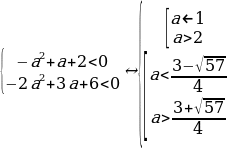

Ответ: 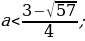
Пример№7: Найдите все значения параметра a, при которых для любого действительного x выполнено неравенство
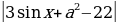
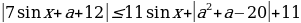
Пусть t=sin x, тогда неравенство запишется в виде
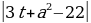
Поскольку -1 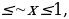
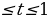
Рассмотрим функции f(t)= 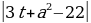
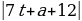
g(t) = 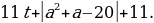
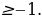
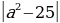
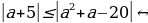
Выражение 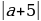
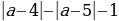
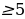
4 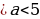
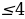
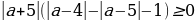
Ответ: 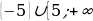
Пример№8: Найдите все значения параметра а, при которых для любого действительного значения х выполнено неравенство
2а – 4 + а(3 – sin 2 x) 2 + cos 2 x ОДЗ: х ∈R, a ∈R. Пусть sin 2 x = t, | t | ≤ 1
2а – 4 + а(3 – t) 2 + 1 — t at 2 – (6a + 1) + 11a – 3 Найдем все значения параметра а, при которых f(t) = at 2 – (6a + 1) + 11a – 3 будет отрицательным при любом | t | ≤ 1.
1) а = 0, f(t) = — t – 3 меньше нуля для любых | t | ≤ 1
2) а 0, 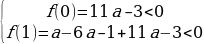
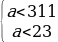
3) а а) D = 1 + 24а – 8а 2
а б) t1 ≤ t2 а D ≥ 0,
t0 = 6a+12af(0) = 11а – 3 a≤0.
в) 1 t1 ≤ t2
а D ≥ 0,
6a+12a1,
f(1) = 6а – 4 ⊘
Ответ: а ∈ (-∞; 311).
Пример№9: Найдите все значения параметра а, при каждом из которых множество решений неравенства 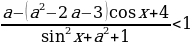
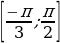
Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству 
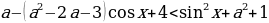
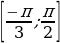
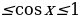
Пусть cos x = t, тогда sin 2 x =1-2t 2 и неравенство принимает вид
a – (a 2 – 2a -3)t + 4 
t 2 – (a 2 – 2a -3)t – a 2 + a + 2 
Введем функцию f(t) = t 2 – (a 2 – 2a -3)t – a 2 + a + 2
(рис. 7)
Для того, чтобы множество решений неравенства
t 2 – (a 2 – 2a -3)t – a 2 + a + 2 
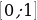



(рис. 8)
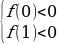

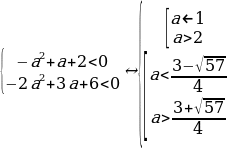

Ответ: 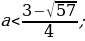
Выводы по второй главе
Во второй главе были приведены решения тригонометрических уравнений и неравенств с параметрами. Рассмотрены пять примеров решения тригонометрических уравнений с параметрами. Задания звучали в двух вариациях: «при каких значения параметра…» и «решите уравнение и найдите значение параметра». Также были разобраны четыре тригонометрических неравенства с параметром. Неравенства, которые были взяты из второй части ЕГЭ, у подобных неравенств задание звучало, не в классическом виде «найдите значение параметра…», а была поставлена дополнительная задача в отборке найденного параметра в заданном отрезке. К каждому примеру было предложено подробный разбор решения.
Исследовательская работа по теме «Тригонометрические уравнения. Способы выбора корней»
Школьный курс алгебры и начала анализа 10 — 11 классы . Исследовательская работа по теме «Тригонометрические уравнения. Способы выбора корней», выполненная ученицей 11 класса Толстых Владиславой под руководством учителя математики Исаковой Т.И. Работа может использована при подготовке к ЕГЭ
Скачать:
| Вложение | Размер |
|---|---|
| trigonometricheskie_uravneniya_sposoby_otbora_korney_22.03.17.doc | 630 КБ |
| trigonometricheskie_uravneniya_sposoby_otbora_korney.ppt | 799 КБ |
Предварительный просмотр:
Региональная научно-практическая конференция
для молодежи и школьников «Шаг в будущее, Сибирь!»
Способы выбора корней
Толстых Владислава, ученица 11класса
Муниципальное казённое обще – образовательное учреждение Средне –Муйская средняя общеобразовательная школа Усть — Удинского района Иркутской области
Исакова Тамара Ивановна, учитель математики, высшей квалификационной категории. МКОУ Средне – Муйская СОШ Усть Удинского района Иркутской области
с. Средняя Муя, 2017год
Из истории происхождения
Типы тригонометрических уравнений
Способы отбора корней в тригонометрических уравнениях
Практические применения тригонометрии
Актуальность темы: Почему я выбрала тему «Тригонометрические уравнения»?
Почему я выбрала тему «Тригонометрические уравнения»?
Тригонометрические уравнения – это одна из сложнейших тем математики, которая выходит на Единый Государственный Экзамен. Очень многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и выбирать корни, принадлежащие отрезку. Немаловажно знать, тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Следует отметить применение тригонометрии в следующих областях: техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ), компьютерная томография, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография, геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Каждого изучающего математику, интересует как и где применяются полученные знания. Ответ на этот вопрос и дает данная работа.
Методы и приемы :
Гипотеза : Существует две гипотезы:
Выводы : Выполняя исследовательскую работу
1. Из истории происхождения
Слово тригонометрия составилось из двух греческих слов: τρίγονον (тригонон-треугольник) и и μετρειν (метрейн — измерять ) в буквальном переводе означает измерение треугольников .
Именно эта задача- измерение треугольников или, как принято теперь говорить, решение треугольников, т.е. определение всех сторон и углов треугольника по трем его известным элементам (стороне и двум углам, двум сторонам и углу или трем сторонам)- с древнейших времен составляла основу практических приложений тригонометрии.
Как и всякая другая наука, тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач. Первые этапы развития тригонометрии тесно связаны с развитием астрономии. Большое влияние на развитие астрономии и тесно связанной с ней тригонометрии оказали потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил. Значительную роль в развитии тригонометрии сыграла потребность в составлении географических карт и тесно связанная с этим необходимость правильного определения больших расстояний на земной поверхности.
Основополагающее значение для развития тригонометрии в эпоху ее зарождения имели работы древнегреческого астронома Гиппарха (середина II века до н.э.). Тригонометрия как наука, в современном смысле этого слова не было не только у Гиппарха, но и у других ученых древности, так как они еще не имели понятия о функциях углов и даже не ставили в общем виде вопроса о зависимости между углами и сторонами треугольника. Но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. При этом основным средством получения нужных результатов было умение вычислять длины круговых хорд на основании известных соотношений между сторонами правильных трех-, четырех-, пяти- и десятиугольника и радиусом описанного круга.
Гиппарх составил первые таблицы хорд, т.е. таблицы, выражающие длину хорды для различных центральных углов в круге постоянного радиуса. Это были, по существу, таблицы двойных синусов половины центрального угла. Впрочем, оригинальные таблицы Гиппарха (как и почти все им написанное) до нас не дошли, и мы можем составить себе о них представление главным образом по сочинению «Великое построение» или ( в арабском переводе) « Альмагест» знаменитого астронома Клавдия Птолемея , жившего в середине II века н.э.
Птолемей делил окружность на 360 градусов, а диаметр- на 120 частей. Он считал радиус равным 60 частям(60 ′′ ). Каждую из частей он делил на 60 ′ , каждую минуту на 60 ′′ , секунду на 60 терций (60 ′′′ ) и т.д., применяя указанное деление, Птолемей выражал сторону правильного вписанного шестиугольника или хорду, стягивающую дугу в 60 ° в виде 60 частей радиуса (60 ч ), а сторону вписанного квадрата или хорду в 90 ° приравнивал числу 84 ч 51 ′ 10 ″ .Хорду в 120 ° — сторону вписанного равностороннего треугольника- он выражал числом 103 ч 55 ′ 23 ″ и т.д. Для прямоугольного треугольника с гипотенузой, равной диаметру круга, он записывал на основании теоремы Пифагора: (хорда α ) 2 +(хорда | 180- α| ) 2 =(диаметру) 2 , что соответствует современной формуле sin 2 α +cos 2 α =1.
«Альмагест» содержит таблицу хорд через полградуса от 0 ° до 180 ° , которая с нашей современной точки зрения представляет таблицу синусов для углов от 0 ° до 90 ° через каждые четверть градуса.
В основе всех тригонометрических вычислений у греков лежала известная еще Гиппарху теорема Птолемея: «прямоугольник, построенный на диагоналях вписанного в круг четырехугольника, равен сумме прямоугольников, построенных на противолежащих сторонах» (произведение диагоналей равно сумме произведений противоположных сторон). Пользуясь этой теоремой, греки умели (с помощью теоремы Пифагора) по хордам двух углов вычислить хорду суммы (или хорду разности) этих углов или хорду половины данного угла, т.е. умели получать результаты, которые мы получаем теперь по формулам синуса суммы (или разности) двух углов или половины угла.
Новые шаги в развитии тригонометрии связаны с развитием математической культуры народов Индии, Средней Азии и Европы (V-XII) .
Важный шаг вперед в период с V по XII век был сделан индусами, которые в отличие от греков стали рассматривать и употреблять в вычислениях уже не целую хорду ММ ′ ( см. чертеж) соответствующего центрального угла, а только ее половину МР, т. е. то, что мы теперь называем линией синуса α — половины центрального угла.
Наряду с синусом индусы ввели в тригонометрию косинус, точнее говоря, стали употреблять в своих вычислениях линию косинуса. (термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого « синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90 ° . «Синус дополнения» или ( по латыни) sinus complementi стали сокращенно записывать как sinus co или co-sinus).
Им были известны также соотношения cos α =sin(90 ° — α ) и sin 2 α +cos 2 α =r 2 , а также формулы для синуса суммы и разности двух углов.
Следующий этап в развитии тригонометрии связан со странами
Средней Азии, Ближнего Востока, Закавказья(VII-XV в.)
Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии, причем тригонометрия сформировалась в особую математическую дисциплину в значительной мере именно в трудах среднеазиатских ученых. Из числа сделанных ими важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индусам.
Решая задачу об определении высоты Солнца S по тени b вертикально стоящего шеста a (см чертеж), сирийский астроном ал-Баттани (Хв.)пришел к выводу, что острый угол ϕ в прямоугольном треугольнике определяется отношением одного катета к другому, и вычислил небольшую таблицу котангенсов через 1 ° . Точнее говоря, он вычислил длину тени b=a ⋅ =a ⋅ ctg ϕ шеста определенной длины (а=12) для ϕ =1 ° ,2 ° ,3 ° ……
Абу-ль-Вафа из Хоросана, живший в Х веке (940-998), составил аналогичную «таблицу тангенсов», т.е. вычислил длину тени b=a ⋅ =a ⋅ tg ϕ , отбрасываемой горизонтальным шестом определенной длины ( а=60) на вертикальную стену (см. чертеж).
Следует отметить, что сами термины «тангенс» (в буквальном переводе- «касающийся») и «котангенс» произошли из латинского языка и появились в Европе значительно позднее (XVI-XVIIвв.). Среднеазиатские же ученые называли соответствующие линии «тенями»: котангенс- «первой тенью», тангенс- «второй тенью».
Абу-ль-Вафа дал совершенно точное геометрическое определение линии тангенса в тригонометрическом круге и присоединил к линиям тангенса и котангенса линии секанса и косеканса. Он же выразил (словесно) алгебраические зависимости между всеми тригонометрическими функциями и, в частности, для случая, когда радиус круга равен единице. Этот чрезвычайно важный случай был рассмотрен европейскими учеными на 300 лет позднее. Наконец, Абу-ль-Вафа составил таблицу синусов через каждые 10 ′ .
В трудах среднеазиатских ученых тригонометрия превратилась из науки, обслуживающей астрономию, в особую математическую дисциплину, представляющую самостоятельный интерес.
Тригонометрия отделяется от астрономии и становится самостоятельной наукой. Это отделение обычно связывают с именем азербайджанского математика Насирэддина Туси (1201-1274).
Впервые в европейской науке стройное изложение тригонометрии дано в книге «О треугольниках разных родов», написанной Иоганном Мюллером , более известным в математике под именем Региомонтана(1436-1476). Он обобщает в ней методы решения прямоугольных треугольников и дает таблицы синусов с точностью до 0,0000001. При этом замечательно то, что он полагал радиус круга равным 10 000 000 или 10 000, т.е. выразил значения тригонометрических функций в десятичных дробях, перейдя фактически от шестидесятиричной системы счисления к десятичной.
Английский ученый XIV века Брадвардин (1290-1349) первый в Европе ввел в тригонометрические вычисления котангенс под названием «прямой тени» и тангенс под названием «обратной тени».
На пороге XVIIв. В развитии тригонометрии намечается новое направление- аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур и учение о тригонометрических функциях строилось на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно становится одной из глав математического анализа. О свойствах периодичности тригонометрических функций знал еще Виет , первые математические исследования которого относились к тригонометрии.
Швейцарский математик Иоганн Бернулли (1642-1727) уже применял символы тригонометрических функций.
В первой половине XIXв. французский ученый Ж.Фурье доказал, что всякое периодическое движение может быть представлено в виде суммы простых гармонических колебаний.
Огромное значение в истории тригонометрии имело творчество знаменитого петербургского академика Леонарда Эйлера (1707-1783), он придал всей тригонометрии современный вид.
В своем труде «Введение в анализ» (1748 г.) Эйлер разработал тригонометрию как науку о тригонометрических функциях, дал ей аналитическое изложение, выведя всю совокупность тригонометрических формул из немногих основных формул.
Эйлеру принадлежит окончательное решение вопроса о знаках тригонометрических функций во всех четвертях круга, вывод формул приведения для общих случаев.
Введя в математику новые функции- тригонометрические, стало целесообразным поставить вопрос о разложении этих функций в бесконечный ряд. Оказывается, такие разложения возможны:
Эти ряды позволяют значительно облегчить составление таблиц тригонометрических величин и для нахождения их с любой степени точности.
Аналитическое построение теории тригонометрических функций, начатое Эйлером, было завершено в работах Н.И.Лобачевского, Гаусса, Коши, Фурье и других.
«Геометрические рассмотрения,- пишет Лобачевский,- необходимы до тех пор в начале тригонометрии, покуда они не послужат к открытию отличительного свойства тригонометрических функций…Отсюда делается тригонометрия совершенно независимой от геометрии и имеет все достоинства анализа».
В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть-учение о тригонометрических функциях -является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть- решение треугольников -рассматривается как глава геометрии.
II. Типы тригонометрических уравнений:
К определению тригонометрического уравнения различные авторы учебных пособий подходят по-разному. Мы назовем тригонометрическим уравнениям равенство тригонометрических выражений, содержащих неизвестное (переменную) только под знаком тригонометрических функций. Уравнения cos 3x=sin; tg(π/2 – 11x) – tg ((3/2)π-5x) = 0; sin 3x+sin 5x = sin 4x и т.д. суть тригонометрические уравнения. Уравнения sin x=(1/2)x; cos 2x = — (1/2)x + (1/3); tg x = x и т.д. не являются тригонометрическими, они относятся к типу трансцендентных уравнений и, как правило, решаются приближенно или графически. Может случиться так, что не является тригонометрическим согласно определению, однако оно может быть сведено к тригонометрическому. Например, 2(x-6) cos 2x=x-6. Мы видим, что x-6 не содержится под знаком тригонометрических функций, однако оно решается аналогически: (x-6) × (2 cos 2x -1)=0, откуда x=6 или cos 2x = (1/2), x=±(π/6)+nπ, nϵZ. Решить тригонометрическое уравнение – значит найти все его корни – все значения неизвестного, удовлетворяющие уравнению. При решении тригонометрических уравнений мы будем пользоваться известными тригонометрическими формулами. Простейшими тригонометрическими уравнениями являются: sin x=′a и cos x=a, где ׀а׀≤1, tg x=a и ctg x=a, где aϵR. Для решения различных видов тригонометрических уравнений необходимо уметь решать простейшие тригонометрические уравнения. Перейдем к рассмотрению решения тригонометрических уравнений различных видов.
1 тип — простейшие тригонометрические уравнения:
а) уравнения вида sin x=a
Уравнение вида sin x=a может иметь решении только при ׀а׀≤1. Известно, что решение этого уравнения находят по обобщенной формуле: x=(-1) n arcsin a+ nπ(1), где nϵZ и (-π/2)≤ arcsin a≤( π/2).
Решение. (2/3)x=(-1) n arcsin(1/2)+nπ, (2/3)x=(-1) n ( π/6) +nπ, x=(-1) n (π/4) +(3/2)nπ, nϵZ.
Ответ: x=(-1) n (π/4) +(3/2)nπ, nϵZ.
Решение. (3π/√x)= (-1) n+1 arcsin (√3/2) +nπ, (3π/√x)= (-1) n+1 (π/3) +nπ, (3/√x)= (-1) n+1 (1/3)+π, √x=(3/(-1) n+1 (1/3)+π) или √x=(9/3n+(-1) n+1 ), x=(81/((-1) n+1 (1/3)+π) 2 ), nϵN. Ответ: x=(81/((-1) n+1 (1/3)+π) 2 ), nϵN.
б) Уравнение вида cos x=a
Уравнение вида cos x=a может иметь решении только при ׀а׀≤1. Известно, что решение этого уравнения находят по обобщенной формуле: x= ±arccos a+ 2nπ, где nϵZ и 0≤ arccos a≤ π
Полезно знать, что arccos (-a) = π- arccos a.
Решение. (5/6)x= ±arccos(√3/2)+ 2nπ, (5/6)x=±( π/6) +2nπ, x=±( π/5) +(12/5)nπ, nϵZ.
Ответ: x=±(π/5) +(12/5)nπ, nϵZ.
Решение. cos(3x-2)=(√2/2), 3x-2 = = ±arccos(√2/2)+ 2nπ, 3x-2=±( π/4) +2nπ, x=(2/3)±(π/5)+ (2/3)nπ, nϵZ. Ответ: x=(2/3)±(π/5)+ (2/3)nπ, nϵZ.
в) Уравнение вида tg x=a, aϵR
Известно, что решение данного уравнения находят по обобщенной формуле: x=arctg a+ nπ, где nϵZ. Полезно помнить, что arctg (-a)= — arctg a.
Решение. 2x=arctg √3+nπ, 2x=( π/3)+ nπ, 2x=(3n+1)( π/3),x=(3n+1)( π/6), nϵZ.
Ответ: x=(3n+1)( π/6), nϵZ.
Решение. (2/3x)= arctg(-1)+ nπ, (2/3x)= -arctg1+ nπ, (2/3x)= (-π/4)+ nπ, (2/3x)= (-π/4)+ nπ, (2/3x)= (4π—1)(π/4), (1/x)= (4π—1)(3π/8), x=(8/(4π—1)3π), nϵZ.
Ответ: x=(8/(4π—1)3π), nϵZ.
г) уравнение вида ctg x=a, aϵ R
Известно, что решение данного уравнения находят по обобщенной формуле: x=arcctg a+ nπ,(5), где nϵZ и 0
При решении простейших уравнений можно использовать тригонометрический круг. Я считаю, что данный способ более рациональный, чем решение тригонометрических уравнений с помощью формулы.
2 тип-уравнения, сводимые к алгебраическим
Это уравнения, сводимые к одной и той же функции относительно одного и того же неизвестного выражения, выходящего только под знак функции.
Тригонометрические уравнение a sin 2 x+ b sin x+c=0, a cos 3 x+ b cos x+c=0; a tg 4 3x+ b tg 2 3x+c=0, a ctg 2 2x+ b ctg 2x+c=0 уже сведены к алгебраическим. Действительно, положив в них соответственно sin x=y, cos x=z, tg 3x=t, ctg 2x= u, получим алгебраические уравнения: ay 2 + by+c=0, az 2 + bz+c=0, at 4 + bt 2 +c=0; au 2 + bu+c=0. Решив каждое из них, найдем sin x, cos x, tg 3x, ctg 2x.
Уравнения a sin 2 x+ b cos x+c=0, a cos 2 x+ b sin x+c=0, a tg x+ b ctg x =0 не являются по виду алгебраическими, но их можно свести к алгебраическим: a cos 2 x- b cos x-(a+c)=0, a sin 2 x- b sin x-(a+c)=0 и a tg x +(b/tg x)=0.
При решении уравнений сводимых к алгебраическим необходимо знать формулы:
1) sin x+cos x=1; 2)tg a =(sin a/cos a); 3) ctg a=( cos a/ sin a); 4) ctg a=(1/tg a)
5)1+tg 2 a=(1/cos 2 a); 6)1+ctg 2 a=(1/sin 2 a); 7) 1+cos 2a=2cos 2 a; 8) 1-cos 2a=2sin 2 a;
9)tg2a=(2 tga/1-tg 2 a); 10) sin2a=(2 tga/1+tg 2 a); 11)cos 2a=(1-tg 2 a/1+tg 2 a);
12)sin2a=2sin a cos a; 13) cos2a= cos 2 a-sin 2 a, или cos2a= 2cos 2 a-1, или cos2a= 1-2sin 2 a;
14) Формулы приведения;
Пример1: Решить уравнение2 sin 2 x + sin x – 1 = 0;
2 sin 2 x + sin x – 1 = 0;
sin x = а, ׀ а ׀ ≤ 1;
D = 9; а 1 = — 1; а 2 = 1 / 2 ;
sin x = -1; sin x = 1 / 2 ;
х 1 = — п / 2 + 2пn, n € N. x 2 = (- 1) k п / 6 + пk, k€ N.
Ответ: — п / 2 + 2пn; (- 1) k п / 6 + пk, n, k € N.
Приме 2: Решить уравнение
3 тип-однородные уравнения
Уравнения a sin x+ b cos x=0; a sin 2 x+b sin x cos x+c cos 2 x=0; a sin 3 x+b sin 2 x cos x+ c sin x cos 2 x+ d cos 3 x=0 и т.д. называют однородными относительно sin x и cos x. Сумма показателей степеней при sin x и cos x у всех членов такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Рассмотренные уравнения имеют соответственно первую, вторую и третью степень. Делением на cos k x, где k-степень однородного уравнения, уравнение приводится к алгебраическому относительно функции tg x.
Рассмотрим уравнение a sin 2 x+b sin x cos x+c cos 2 x=0(1). Разделим уравнение(1) на cos 2 x, получим: a tg 2 x+ b tg x+c=0(2).При a≠0 (1) и (2) равносильны, так как cos x≠0. Если же cos x=0, то из уравнения(1) видно, что и sin x =0, что невозможно, так как теряет смысл тождество .
При решении однородных уравнений применяем схему:
Пример1. Решить уравнение: 3 sin2 x + sin x • cos x = 2 cos2 x;
3 sin 2 x + sin x · cos x = 2 cos 2 x;
3 tq 2 x + tq x = 2; х ≠ п / 2 + пn, n € N.
D = 25; а 1 = — 1; а 2 = 2 / 3 ;
tq x = — 1; tq x = 2 / 3 ;
х 1 = — п / 4 + пn, n € N. x 2 = arctq 2 / 3 + пn, n € N.
Ответ: — п / 4 + пn, arctq 2 / 3 + пn, n € N.
Пример 2. 5 sin x — 2 cos x = 0
Поделим обе части уравнения cos x (или на sin x). Предварительно докажем,
что cos x 0 (или sin x 0). (Пусть cos x = 0, тогда 5 sin x — 2 • 0 = 0, т.е. sin x = 0; но этого не может быть, так как sin 2 x + cos 2 x = 1).
Значит, можно делить на cos x:
5 sin x /cos x — 2 cos x / cos x = 0 / cos x. Получим уравнение
x = arctg 2/5 + n, n = Z.
Ответ: x = arctg 2/5 + n, n = Z.
Аналогично решаются однородные уравнения вида a sin 2 x + b sin x cos x + c cos 2 x = 0, их решение начинается с того, что обе части уравнения делятся на cos 2 x (или на sin 2 x).
Пример 3. 12 sin 2 x + 3 sin 2x — 2 cos 2 x = 2.
Данное уравнение не является однородным, но его можно преобразовать в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin 2 x + 2cos 2 x.
Приведя подобные члены, получим уравнение
10sin 2 x + 6sin x cos x — 4 cos 2 x = 0.
(Пусть cos x = 0, тогда 10sin 2 x = 0, чего не может быть, т.к. sin 2 x + cos 2 x = 1, значит, cos x 0).
Разделим обе части уравнения на cos 2 x.
10 tg 2 x +6 tg x — 4 = 0,
tg x = -1 или tg x = 2/5,
x = — /4 + n, n = Z, x = arctg 2/5 + k, k = Z.
Ответ: x 1 = — /4 + n, n = Z, x 2 = arctg 2/5 + k, k = Z.
4 тип- уравнения, решаемые разложением на множители:
При решении уравнений методом разложения нужно пользоваться всеми известными способами разложения на множители алгебраических выражений. Это вынесение за скобки общего множителя, группировка, применение формул сокращенного умножения и деления и искусственные приемы. Необходимо так же знать формулы: 1) sin x+cos x=1; 2)tg a =(sin a/cos a); 3) ctg a=( cos a/ sin a); 4) ctg a=(1/tg a)
5)1+tg 2 a=(1/cos 2 a); 6)1+ctg 2 a=(1/sin 2 a); 7) 1+cos 2a=2cos 2 a; 8) 1-cos 2a=2sin 2 a;
9)tg2a=(2 tga/1-tg 2 a); 10) sin2a=(2 tga/1+tg 2 a); 11)cos 2a=(1-tg 2 a/1+tg 2 a);
12)sin2a=2sin a cos a; 13) cos2a= cos 2 a-sin 2 a, или cos2a= 2cos 2 a-1, или cos2a= 1-2sin 2 a;
14)tg(a±b) = (tg a±tg b)/(1±tg a tg b); 15)sin 3a=3sin a – 4sin 3 a; 16)cos 3 a = 4 cos 3 a – 3 cos a;
Пример2. 2 sin 3 x — cos 2x — sin x = 0
Сгруппируем первый член с третьим, а cos 2x = cos 2 x — sin 2 x.
(2sin 3 x — sin x) – (cos 2 x — sin x) = 0,
Вынесем из выражения, стоящего в первой скобке sin x, а cos 2 x = 1 — sin x.
sin x (2sin 2 x – 1) – (1 — 2 sin 2 x) = 0,
sin x (2sin 2 x – 1) + (2 sin 2 x — 1) = 0,
(2 sin 2 x — 1) • ( sin x + 1) = 0.
2 sin 2 x – 1 = 0
Ответ: x 1 = ± /4 + n, n = Z, x 2 = — /2 +2 k, k = Z.
5 тип-уравнения, решаемые с помощью условия равенства одноименных тригонометрических функций
Многие тригонометрические уравнения могут быть приведены к равенству одноименных тригонометрических функций. Такие уравнения решаются на основании условий равенства одноименных тригонометрических функций, т.е. тех условий, которым должны удовлетворять два угла: a и b, если a) sin a =sin b, б) cos a= cos b, в) tg a = tg b.
Теорема I. Для того чтобы синусы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: разность этих углов должна равняться π, умноженному на четное число, или сумма этих углов должна равняться π, умноженная на нечетное число,
Теорема II . Для того чтобы косинусы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: разность(сумма) этих углов должна равняться произведению π на четное число.
Теорема II . Для того чтобы тангенсы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: тангенс каждого из данных углов существует и разность этих углов равна числу π, умноженному на целое число.
6 тип- уравнения, решаемые с помощью формул сложения тригонометрических функций:
Для решения данного типа применяются формулы преобразования суммы тригонометрических функций в произведение:
Sin a + sin b= 2 sin((a+b)/2) cos((a-b)/2);
Sin a — sin b= 2 sin((a-b)/2) cos((a+b)/2);
cos a + cos b= 2 cos ((a+b)/2) cos((a-b)/2);
cos a — cos b= 2 sin ((a+b)/2) sin ((b-a)/2) при b>a;
cos a — cos b= 2 sin ((a+b)/2) sin ((a-b)/2) при b
tg a ± tg b = (sin(a+b)/ cos a cos b);
ctg a + ctg b = (sin(a+b)/ sin a sin b);
ctg a — ctg b = (sin(b-a)/ sin a sin b);
В некоторых примерах прийдется применять формулы:
sin (a±b)= sin a cos b± cos a sin b;
cos (a±b)= cos a cos b± sin a sin b;
7 тип- уравнения, решаемые с помощью формул сложения углов и разложения произведения тригонометрических функций в сумму
Формулы сложения углов и разложения произведения тригонометрических функций в сумму:
sin (a±b)= sin a cos b± cos a sin b;
cos (a±b)= cos a cos b± sin a sin b;
tg(a±b) = (tg a±tg b)/(1±tg a tg b);
sin a cos b=(1/2)(sin(a+b)+ sin(a-b));
cos a cos b=(1/2)( cos (a+b)+ cos (a-b));
sin a sin b=(1/2)( cos (a-b)- cos (a+b));
8 тип-уравнения, решаемые с помощью формул понижения степени
Формулы понижения степени:
Sin 2 t=((1- cos 2t)/2)
Cos 2 t=((1+cos 2t)/2)
9 тип- уравнения вида a sin x+b cos x= c
В уравнении a sin x+b cos x= c a, b и c- любые действительные числа. Если а=b=0, а с≠0, то уравнение теряет слысл; если же а=b=с=0, то x- любое действительное число, т.е. уравнение обращается в тождество. Например, √3 sin x + cos x=1. Разделив обе части уравнения на 2, получим (√3/2) sin x + (1/2)cos x=(1/2), т.е. sin(x+(π/6))=1/2 или cos(x-(π/6))= 1/2. Уравнение sin x+ cos x=1 можно решать по крайней мере четырьмя способами. Например, разделив обе части уравнения на √2, получив: (1/√2) sin x+(1/√2) cos x= (1/√2), sin(x+(π/4))= (2/√2) и т.д.
Рассмотрим уравнение a sin x+b cos x= c, у которого произвольные коэффициенты. Такие уравнения решаются разными способами.
1-й способ решения уравнения a sin x+b cos x= c – введение вспомогательного угла.
Мы знаем, что если a 2 +b 2 =1, то существует такой угол как φ, а= cos φ, b= sin φ или наоборот. Для решения уравнения a sin x+b cos x= c вынесем за скобки множителем выражение √( a 2 +b 2 ). Получим: √( a 2 +b 2 )((a/√( a 2 +b 2 )) sin x+(b/√( a 2 +b 2 )) cos x)=c. Поскольку (((a/√( a 2 +b 2 )) sin x) 2 +((b/√( a 2 +b 2 )) cos x)) 2 =1, то первое число (a/√( a 2 +b 2 )) можно принять за косинус некоторого угла φ, а второе (b/√( a 2 +b 2 )) — за синус того же угла φ, т.е. (a/√( a 2 +b 2 ))= cos φ, (b/√( a 2 +b 2 )) = sin φ. В таком случае уравнение примет вид: √( a 2 +b 2 )( cos φ sin x+ sin φ cos x)= c или √( a 2 +b 2 ) sin(φ+x), откуда sin(φ+x)= (с/√( a 2 +b 2 )). Это уравнение имеет решение, если a 2 +b 2 =с 2 , тогда φ+x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ, x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ- φ, nϵZ. Угол φ находится из равенства tg φ =( sin φ/ cos φ) =(b/a), откуда φ=arctg(b/a). Ответ: x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ- arctg(b/a), nϵZ.
Пример: Решим уравнение 12cosx — 5sinx = -13
Решение: разделим обе части уравнения на , получим
Одним из решений системы cos = 12/13, sin = 5/13 является =arccos(12/13). Учитывая это, запишем уравнение в виде:
и, применив формулу для косинуса суммы аргументов, получим
2-й способ решения уравнения a sin x+b cos x= c – метод рационализации.
Известно, что если α≠π(2n+1), nϵZ, то sin α, cos α, tg α выражаются рационально через tg(α/2), т.е. sin α=( 2tg(α/2)/1+ tg 2 (α/2)), cos α=(1- tg 2 (α/2)/ 1+ tg 2 (α/2)), и tg α=( 2tg(α/2)/1- tg 2 (α/2)).
Метод рационализации заключается в следующем: вводится вспомогательное неизвестное так, чтобы после подстановки получилось рациональное уравнение относительно этого вспомогательного неизвестного. Рассмотрим уравнение a sin x+b cos x= c, которое можно переписать так: a( 2tg(α/2)/1+ tg 2 (α/2))+b(1- tg 2 (α/2)/ 1+ tg 2 (α/2))=c. Положим tg(x/2)=t, тогда получим: a( 2t/1+ t 2 )+b(1- t 2 / 1+ t 2 )=c. Это уравнение – рациональное относительно t. Умножим обе части уравнения на 1+ t 2 ≠0 при tϵR, получим: (b+c)t 2 -2at+(c-b)=0(2), (D/4)=a 2 -(c-b)(c+b)= a 2 +b 2 -с 2 . Полагаем, что a+b≠0 или с≠-b, тогда t 1.2 =((a±√( a 2 +b 2 -с 2 )/(b+c))(3). Значение t- действительные, если a 2 +b 2 ≥с 2 .
Если уравнение(2) с=-b, то оно обратится в уравнение первой степени: -2at-2b=0, t=-(b/a), т.е. tg(x/2)=- (b/a), x=-2 arctg(b/a)+2nπ. Выражение для вспомогательного неизвестного t= tg(x/2) теряет смысл при (x/2)= (π/2)+nπ, т.е. x=(2n+1)π. Решения уравнения(1) вида x=(2n+1)π (если такие решения существуют) могут быть потеряны. Подставив x=(2n+1)π в уравнение (1), получим a sin(2n+1)π +b cos(2n+1)π = c; a·0+b(-1)=c; с=-b. Том случае уравнение (1) имеет множество решений вида x=(2n+1)π, nϵZ.
3-й способ решения уравнения a sin x+b cos x= c.
Можно возвести обе части уравнения в квадрат и привести его к однородному. Этот способ неприемлем, так как получаются посторонние корни.
4-й способ решения уравнения a sin x+b cos x= c.
Универсальная тригонометрическая подстановка
Многие тригонометрические уравнения можно решить с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку не определен в точках , поэтому в таких случаях нужно проверять, являются ли углы , корнями исходного уравнения.
Пример. Решим уравнение
Решение:
Обращение к функции предполагает, что , то есть , .
По формулам универсальной тригонометрической подстановки исходное уравнение примет вид:
|: 2
, ;
IV. Способы отбора корней в тригонометрических уравнениях
1 способ: Арифметический(непосредственная подстановка корней в уравнение и имеющиеся ограничения)
2 способ. Геометрический способ(отбор корней тригонометрического уравнения на числовой прямой )
Отмечаю значения х при n,k,m=0 на числовой прямой и отрезок[-(3π/2); (π/2)]
Измеряю период 2 π с помощью линейки(период функции, входящей в уравнение) и откладываю период с помощью линейки вправо, влево.
Определяю значения углов, принадлежащих данному отрезку.
3 способ: Геометрический способ(отбор корней тригонометрического уравнения на числовой окружности)
Выбор корней уравнения 2 sin2x+ sinx-1=0, принадлежащих отрезку[π/2; 2π] покажу на тригонометрическом круге
4 способ: Функционально-графический способ
В одной системе координат строим графики функции у=sin x и у=-1; у=sin x и у=1/2. Показываем отрезок [-3п/2;п/2]. Находим точки пересечения графиков функций у=sin x и у=-1; у=sin x и у=1/2, входящих в промежутке [-3п/2;п/2].
х= -7п/6; х= -п/2; х=п/6 являются решением уравнения
5 способ: Алгебраический (решение неравенства относительно неизвестного целочисленного параметра и вычисления корней)
Считаю лучшим способом — это алгебраический (решение неравенства относительно неизвестного целочисленного параметра и вычисления корней)
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Следует отметить применение тригонометрии в следующих областях: техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ), компьютерная томография, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография, геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Приведу несколько примеров из практики, например: тригонометрия в медицине и биологии.
Модель биоритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула, получившая название тегеранской, была представлена широкой научной общественности на 14-й конференции географической медицины и затем — на 28-й конференции по вопросам применения компьютерной техники в кардиологии, состоявшейся в Нидерландах. Эта формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории
Результаты нового исследования, как можно предположить, окажутся небезынтересны инженерам, конструирующим системы навигации для роботов, а также специалистам, которые работают над созданием максимально реалистичных виртуальных моделей. Возможны и приложения в области медицины, при реабилитации пациентов с повреждениями определенных областей мозга.
Выполняя исследовательскую работу, выяснила какое значение имеют тригонометрические уравнения в жизни человека и как они работают в стране. Рассмотрела способы выбора корней уравнения принадлежащих отрезку из раздела «ЕГЭ по математике» Доказала, что в современном мире прожить без знаний тригонометрический уравнений невозможно. Чтобы быть хорошими специалистами, уметь разбираться в большом потоке информации, необходимо знать тригонометрические уравнения. Изучение столь важной и интересной темы дает положительную мотивацию для самообразования
http://multiurok.ru/files/kursovaia-rabota-po-teme-trigonometricheskie-uravn.html
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2017/11/28/issledovatelskaya-rabota-po-teme