Решение тригонометрических уравнений и неравенств теория

Тригонометрические уравнения

Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.

Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.

$1$ радиан $=<180>/<π>≈57$ градусов

Значения тригонометрических функций некоторых углов

$α$	$0$	$<π>/<6>$	$<π>/<4>$	$<π>/<3>$	$<π>/<2>$	$π$
$sinα$	$0$	$<1>/<2>$	$<√2>/<2>$	$<√3>/<2>$	$1$	$0$
$cosα$	$1$	$<√3>/<2>$	$<√2>/<2>$	$<1>/<2>$	$0$	$-1$
$tgα$	$0$	$<√3>/<3>$	$1$	$√3$	$-$	$0$
$ctgα$	$-$	$√3$	$1$	$<√3>/<3>$	$0$	$-$

Периоды повтора значений тригонометрических функций

Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$

Знаки тригонометрических функций по четвертям

Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.

Чтобы правильно раскрыть формулы приведения необходимо помнить что:

если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется (если же в формуле содержатся углы $90°$ и $270°$ ($π/2$ и $<3π>/<2>$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.

Преобразовать $сos (90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.

Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому перед $sinα$ нужен знак $-$.

$сos (90° + α)= — sinα$ — это конечный результат преобразования

Вычислить $cos 840°$

У косинуса период повторения $2π$ или $360°$, мы можем из угла вычитать количество градусов кратное периоду.

$cos 840°=cos(720°+120°)=cos 120°$

По формуле приведения представим $120°$ как $90°+30°$

$cos(90°+30°) = -sin30= — 0.5$

Четность тригонометрических функций

Косинус четная функция: $cos(-t)=cos t$

Синус, тангенс и котангенс, нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$

Тригонометрические тождества

3. $sin^ <2>α+cos^ <2>α=1$ (Основное тригонометрическое тождество)

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

Вычислить $sin t$, если $cos t = <5>/ <13>; t ∈(<3π>/<2>;2π)$

Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(<3π>/<2>;2π)$ — это четвертая четверть, то синус в ней имеет знак минус.

Обратные тригонометрические функции и простейшие тригонометрические уравнения.

Арккосинус

Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $[0;π]$, косинус которого равен $а$.

$arcos(-a) = π-arccos⁡a$, где $0≤а≤1$

Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение

$cos t =1, t = 2πk;k∈Z$

$cos t = 0, t = <π>/<2>+πk;k∈Z$

$cos t = -1, t=π+2πk;k∈Z$

Найдите наименьший положительный корень уравнения сos $<2πx>/<3>=-<√3>/<2>$

Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на $<2π>/<3>$

Чтобы найти наименьший положительный корень, подставим вместо к целые значения

Нам подходит $1.25$ – это и есть результат

Арксинус

Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-<π>/<2>;<π>/<2>]$, синус которого равен $а$.

$arcsin(-a)= — arcsin a$, где $0≤а≤1$

Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:

1. $t_1 = arcsin a+2πk;k∈Z$

$t_2 = (π- arcsin a)+ 2πk;k∈Z$

Арктангенс

$arctg a$ — это такое число, из отрезка $[-<π>/<2>;<π>/<2>]$, тангенс которого равен $а.$

$arctg(-a)= — arctg a$

Уравнение $tg t = a$ имеет решение $t= arctg a+πk;k∈Z$

Простейшие тригонометрические уравнения (задание 5) и неравенства

$\blacktriangleright$ Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
$\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b$ , которые имеют смысл при $-1\leq a\leq 1,\quad b\in \mathbb$ .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен $1$ ).

Рассмотрим несколько примеров:

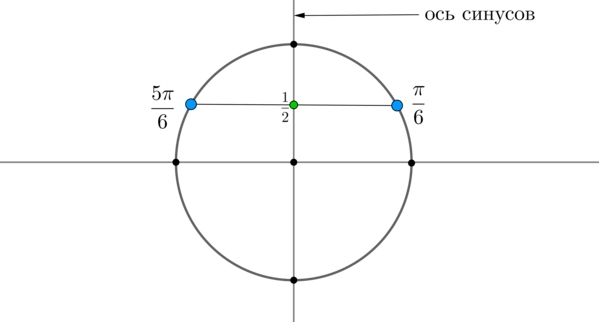
Пример 1. Решить уравнение $\sin x=\dfrac12$ .

Найдем на оси синусов точку $\dfrac12$ и проведем прямую параллельно оси $Ox$ до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен $\dfrac12$ . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$ . Тогда в нашем случае это углы $\dfrac<\pi>6$ и $\dfrac<5\pi>6$ . Все остальные углы можно получить путем прибавления к данным углам $2\pi\cdot n$ , где $n$ — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются $x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb$ .

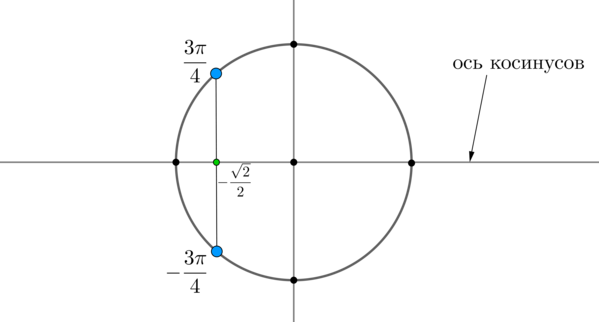
Пример 2. Решить уравнение $\cos x=-\dfrac<\sqrt2><2>$ .

Найдем на оси косинусов точку $-\dfrac<\sqrt2><2>$ и проведем прямую параллельно оси $Oy$ до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен $-\dfrac<\sqrt2><2>$ . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$ . Тогда в нашем случае это углы $\dfrac<3\pi>4$ и $-\dfrac<3\pi>4$ . Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$ , где $n$ — целое число.

Таким образом, решением являются $x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb$ .

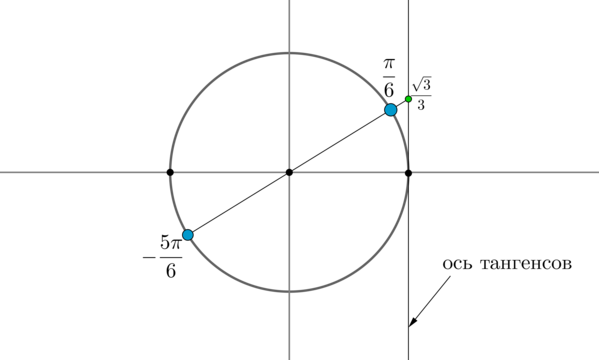
Пример 3. Решить уравнение $\mathrm\,x=\dfrac<\sqrt3>3$ .

Найдем на оси тангенсов точку $\dfrac<\sqrt3>3$ и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен $\dfrac<\sqrt3>3$ .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$ . Тогда в нашем случае это углы $\dfrac<\pi>6$ и $-\dfrac<5\pi>6$ . Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$ , где $n$ — целое число, или путем прибавления к одному из данных углов $\pi n$ .

Таким образом, решением являются $x=\dfrac<\pi>6+\pi n, \ n\in \mathbb$ .

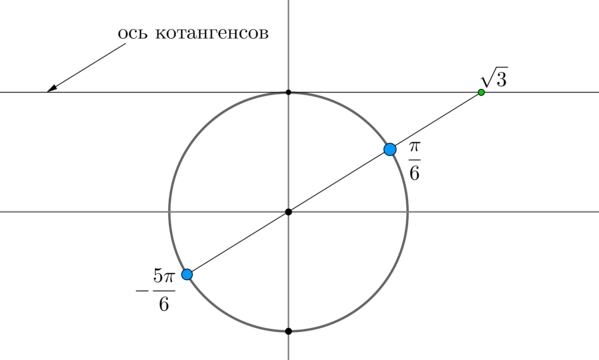
Пример 4. Решить уравнение $\mathrm\,x=\sqrt3$ .

Найдем на оси котангенсов точку $\sqrt3$ и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен $\sqrt3$ . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$ . Тогда в нашем случае это углы $\dfrac<\pi>6$ и $-\dfrac<5\pi>6$ . Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$ , где $n$ — целое число, или путем прибавления к одному из данных углов $\pi n$ .

Таким образом, решением являются $x=\dfrac<\pi>6+\pi n, \ n\in \mathbb$ .

$\blacktriangleright$ Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для $\sin x=a$ записывают как $x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb$ .

$\blacktriangleright$ Любые уравнения вида $\mathrm\,\big(f(x)\big)=a$ , (где $\mathrm$ — одна из функций $\sin, \ \cos, \ \mathrm,\ \mathrm$ , а аргумент $f(x)$ — некоторая функция) сводятся к стандартным уравнениям путем замены $t=f(x)$ .

Пример 5. Решить уравнение $\sin<(\pi x+\dfrac<\pi>3)>=1$ .

Сделав замену $t=\pi x+\dfrac<\pi>3$ , мы сведем уравнение к виду $\sin t=1$ . Решением данного уравнения являются $t=\dfrac<\pi>2+2\pi n, n\in\mathbb$ .

Теперь сделаем обратную замену и получим: $\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n$ , откуда $x=\dfrac16+2n,\ n\in\mathbb$ .

Если $n$ точек, являющихся решением уравнения или системы, разбивают окружность на $n$ равных частей, то их можно объединить в одну формулу: $x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb$ , где $\alpha$ — один из этих углов.

Рассмотрим данную ситуацию на примере:

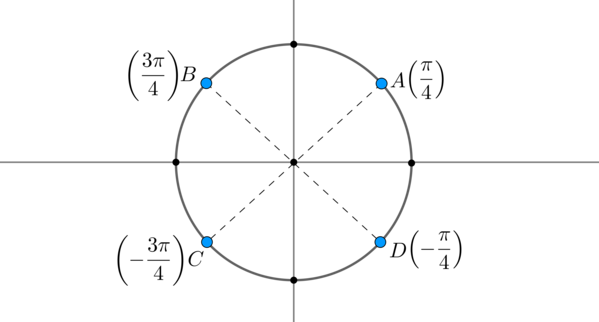
Пример 6. Допустим, решением системы являются $x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb$ . Отметим эти точки на окружности:

Заметим, что длины дуг $\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over$ равны $\dfrac<\pi>2$ , то есть эти точки разбили окружность на $4$ равных части. Таким образом, ответ можно записать в виде одной формулы: $x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb$ .

где $\lor$ — один из знаков $\leq,\ ,\ \geq$ .

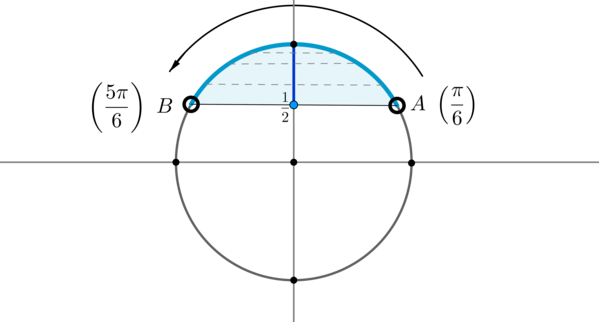
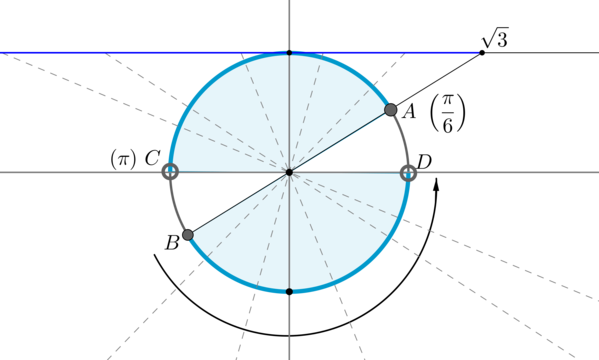
Пример 7. Изобразить на окружности множество решений неравенства $\sin x >\dfrac12$ .

Для начала отметим на окружности корни уравнения $\sin x =\dfrac12$ . Это точки $A$ и $B$ . Все точки, синус которых больше $\dfrac12$ , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это $A$ , а конец — $B$ .

Выберем в точке $A$ любой угол, например, $\dfrac<\pi>6$ . Тогда в точке $B$ необходимо выбрать угол, который будет больше $\dfrac<\pi>6$ , но ближайший к нему, и чтобы синус этого угла также был равен $\dfrac12$ . Это угол $\dfrac<5\pi>6$ . Тогда все числа из промежутка $\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)$ являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид $\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb$ , т.к. у синуса период $2\pi$ .

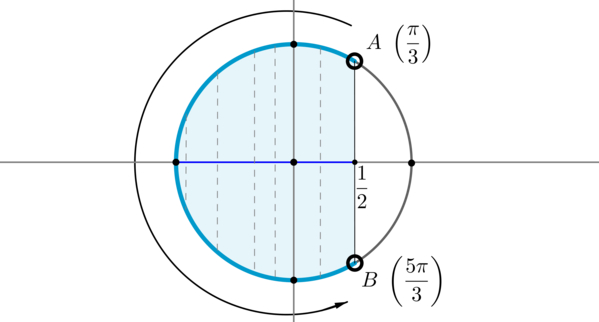
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

Для начала отметим на окружности корни уравнения $\cos x =\dfrac12$ . Это точки $A$ и $B$ . Все точки, косинус которых меньше $\dfrac12$ , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это $A$ , а конец — $B$ .

Выберем в точке $A$ любой угол, например, $\dfrac<\pi>3$ . Тогда в точке $B$ необходимо выбрать угол, который будет больше $\dfrac<\pi>3$ , но ближайший к нему, и чтобы косинус этого угла также был равен $\dfrac12$ . Это угол $\dfrac<5\pi>3$ . Тогда все числа из промежутка $\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)$ являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид $\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb$ , т.к. у косинуса период $2\pi$ .

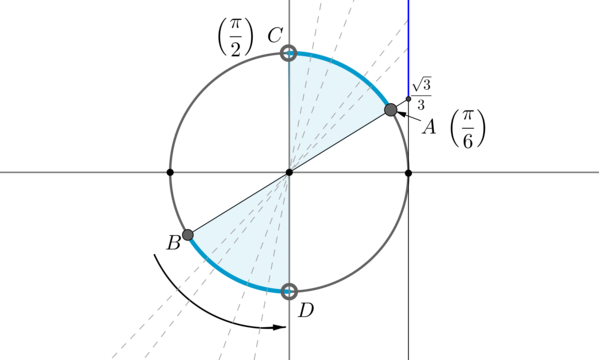
Пример 9. Изобразить на окружности множество решений неравенства $\mathrm\, x \geq \dfrac<\sqrt<3>>3$ .

Для начала отметим на окружности корни уравнения $\mathrm\, x = \dfrac<\sqrt<3>>3$ . Это точки $A$ и $B$ . Все точки, тангенс которых больше или равен $\dfrac<\sqrt<3>>3$ , находятся на выделенных дугах, причем точки $C$ и $D$ выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, $\buildrel\smile\over$ . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол $\dfrac<\pi>2$ , тогда начало дуги — это угол $\dfrac<\pi>6$ (угол должен быть меньше $\dfrac<\pi>2$ , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал $\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)$ . А все решения данного неравенства будут иметь вид $\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb$ , т.к. у тангенса период $\pi$ .

Пример 10. Изобразить на окружности множество решений неравенства $\mathrm\, x \leq \sqrt<3>$ .

Для начала отметим на окружности корни уравнения $\mathrm\, x = \sqrt<3>$ . Это точки $A$ и $B$ . Все точки, котангенс которых меньше или равен $\sqrt<3>$ , находятся на выделенных дугах, причем точки $C$ и $D$ выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, $\buildrel\smile\over$ . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол $\pi$ , тогда начало дуги — это угол $\dfrac<\pi>6$ (угол должен быть меньше $\pi$ , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал $\Big[\dfrac<\pi>6;\pi\Big)$ . А все решения данного неравенства будут иметь вид $\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb$ , т.к. период котангенса $\pi$ .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

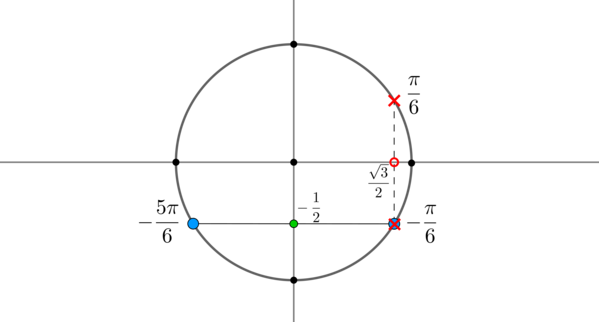
Пример 11. Найти корни уравнения $\sin x=-\dfrac12$ , если $\cos x\ne \dfrac<\sqrt3>2$ .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются $x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb$ , решением второго являются $x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb$ . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка $x= -\dfrac<\pi>6+2\pi n$ не подходит. Следовательно, ответом будут только $x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb$ .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему $\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end$

Решением уравнения являются $x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb$ . Подставим в неравенство $\sin x+\cos x>0$ по очереди оба корня:

$\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0$ , следовательно, корень $x_1$ нам подходит;
$\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2$ нам не подходит.

Таким образом, решением системы являются только $x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb$ .

Алгебраический способ.

Пример 13. Найти корни уравнения $\sin x=\dfrac<\sqrt2>2$ , принадлежащие отрезку $[0;\pi]$ .

Решением уравнения являются $x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb$ . Для того, чтобы отобрать корни, решим два неравенства: $0\leq x_1\leq\pi$ и $0\leq x_2\leq\pi$ :

$0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38$ . Таким образом, единственное целое значение $n$ , удовлетворяющее этому неравенству, это $n=0$ . При $n=0$ $x_1=\dfrac<\pi>4$ — входит в отрезок $[0;\pi]$ .

Аналогично решаем неравенство $0\leq x_2\leq\pi$ и получаем $n=0$ и $x_2=\dfrac<3\pi>4$ .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно $x$ и $y$ тогда и только тогда, когда $c$ делится на $НОД(a,b)$ .

Пример: Уравнение $2x+4y=3$ не имеет решений в целых числах, потому что $3$ не делится на $НОД(2,4)=2$ . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — $3$ , то есть нечетное число.

Пример: Решить уравнение $3x+5y=2$ . Т.к. $НОД(3,5)=1$ , то уравнение имеет решение в целых числах. Выразим $x$ через $y$ :

Число $\dfrac<2-2y>3$ должно быть целым. Рассмотрим остатки при делении на $3$ числа $y$ : $0$ , $1$ или $2$ .
Если $y$ при делении на $3$ имеет остаток $0$ , то оно записывается как $y=3p+0$ . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если $y$ при делении на $3$ имеет остаток $1$ , то оно записывается как $y=3p+1$ . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда $y=3p+1$ , а $x=\dfrac<2-2y>3-y=-5p-1$ .

Ответ: $(-5p-1; 3p+1), p\in\mathbb$ .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые $n$ и $k$ , при которых совпадают решения в сериях $\pi+6\pi n$ и $4\pi k$ :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. $НОД(4,6)=2$ и $1$ не делится на $2$ , то данное уравнение не имеет решений в целых числах.

Найдем целые $m$ и $k$ , при которых совпадают решения в сериях $2\pi +6\pi m$ и $4\pi k$ :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим $k=\frac<3m+1>2=m+\frac2$ .

Возможные остатки при делении $m$ на $2$ — это $0$ или $1$ .
Если $m=2p+0$ , то $\frac2=\frac<2p+1>2=p+\frac12\ne $ целому числу.
Если $m=2p+1$ , то $\frac2=\frac<2p+1+1>2=p+1= $ целому числу.

Значит, $m=2p+1$ , тогда $k=3p+2$ , $p\in\mathbb$ .

Подставим либо $m$ , либо $k$ в соответствующую ему серию и получим окончательный ответ: $x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb$ .

Методическое пособие для студентов. Решение тригонометрических уравнений и неравенств.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Министерство образования и науки Самарской области

Министерство имущественных отношений Самарской области

Государственное бюджетное профессиональное

образовательное учреждение Самарской области

«Чапаевский губернский колледж им. О. Колычева»

Организация самостоятельной деятельности студентов при изучении темы «Решение тригонометрических уравнений и неравенств»

для студентов 1 курса по профессиям Сварщик (ручной и частично механизированной сварки (наплавки);

г.о.Чапаевск, 2017 г.

Публикуется на основании решения

ГБПОУ СОЧГК им. О. Колычева

Протокол № __8_от _20.04.2017

Организация самостоятельной деятельности студентов при изучении темы «Решение тригонометрических уравнений и неравенств» по дисциплине «Математика» для студентов 1 курса, И.В. Ямбаева – Чапаевск: ГБПОУ СОЧГК им.О. Колычева, 2017, 26 стр.- 15 экз.

Данное пособие включает в себя материал по организации самостоятельной деятельности студентов при выполнении заданий в ходе практических занятий по дисциплине «Математика», предназначено для преподавателей и студентов СПО.

Составитель: Ямбаева И.В., преподаватель математики высшей квалификационной категории

Рецензент: Ащепкова В.И., заведующий методическим кабинетом ОП СПО ППКРС, заслуженный учитель РФ

им.О. Колычева», 2017

Данный пособие предназначено для организации практических занятий при изучении темы: «Тригонометрические уравнения и неравенства». Оно поможет систематизировать имеющиеся знания и ликвидировать проблемы в них, если такие окажутся.

В сборнике содержится восемь основных тем, которые включают в себя справочный материал, тренинговые задания и задания для самостоятельный работы. Справочный материал содержит формулы и алгоритмы решения тригонометрических уравнений и неравенств. Эти разделы являются как бы консультантом по вопросам теории. Тренинговые задания содержат набор упражнений из учебника « Алгебра и начала анализа». А.Н.Колмогоров; -М.: Просвещение.

Задания для практических занятий составлены в соответствии с требованиями федерального государственного образовательного стандарта среднего профессионального образования к результатам усвоения данной темы.

Предлагаемый материал для сборника применяется преподавателем на уроках изучения темы «Тригонометрические уравнения и неравенства» и на уроках обобщающего повторения при подготовке к госэкзамену в конце второго курса.

Тема: Решение простейших тригонометрических

Материал для составления опорного конспекта:

Примеры решения задач

Практическая часть урока.

Решение №136,№137,№142б,г,№143в.( учебник Алгебра и начала анализа. А.Н.Колмогоров; -М.: Просвещение)

Урок. Практическое занятие. Решение тригонометрических уравнений cos x = a .

Образовательная цель урока: закрепить знания формул корней уравнения cos x = a, закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

1. 12. 2cos (x + = 1

2. 13. 2cos ( — =

3. 14. cos ( — =

5. 6. cos ( x — ) =

7. cos ( 3x — ) =

9. 10. 11. cos ( x + =

Домашнее задание: решение заданий по образцу.

Материал для составления опорного конспекта:

Примеры решения задач

3.Практическая часть урока.

Решение №138,№139,№142а,в,№143а ( учебник Алгебра и начала анализа. А.Н.Колмогоров; -М.: Просвещение)

Урок. Практическое занятие

Решение тригонометрических уравнений sin х = a .

Образовательная цель урока: закрепить знания формул корней уравнения sin х = a, закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

sin x = —

sin

sin ( x + ) =

sin ( x —

sin (2 x +

sin (3 x —

2 sin (

Домашнее задание: решение заданий по образцу

Материал для составления опорного конспекта:

3. Решение частных случаев тригонометрических уравнений

tg х= 1, х = + n , где n

tg х= 0, х = n , где n ,

tg х= -1, х = — + n , где n

с tg х= 1, х = + n , где n

с tg х= 0, х = + n , где n ,

с tg х= -1, х = + n , где n

2. Примеры решения задач

3.Практическая часть урока. Решение №140,№141,№143б,г

Урок. Практическое занятие

Образовательная цель урока: закрепить знания формул корней уравнений tg t = a , с tg t = a , закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

2. ctg

3. tg (2x +

4. ctg (3x —

5. ctg (x +

6. tg (2x —

7. ctg (5x —

8. tg ( x —

9. ctg ( x+

10. ctg ( 2x —

Домашнее задание: решение заданий по образцу

Урок. Примеры решения тригонометрических уравнений.

п.1 Решение тригонометрических уравнений,

отличающихся от простейших

Материал для составления опорного конспекта:

Как правило, решение тригонометрических уравнений сводится к решению простейших уравнений с помощью преобразований тригонометрических выражений, разложения на множители и замены переменных. Если в уравнение, неравенство или тождество переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).

При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:

1.Пробуем привести все тригонометрические функции к одному аргументу.

2.Если удалось привести к одному аргументу, то пробуем все тригонометрические выражения привести к одной функции.

3.Если к одному аргументу удалось привести, а к одной функции — нет, тогда пробуем привести уравнение к однородному.

4.В других случаях переносим все члены в одну сторону и пробуем получить произведение ил используем специальные приемы решения.

Практическая часть урока. Решение №164,165,166,167,168

п.2 Решение тригонометрических уравнений приведением к одной функции

3.Практическая часть урока. Решение №169,170,171,172,173,

Урок. Практическое занятие

Решение тригонометрических уравнений.

Образовательная цель урока: закрепить знания способов решения уравнений , закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения:

а) 2

б) 2

в) 2

г) 2

а) 2

б)

в)

г)

д)

е)

ж)

а)

б)

г)

д)

Домашнее задание: решение заданий по образцу

Урок. Практическое занятие

Решение тригонометрических уравнений.

Задание 1. Решите уравнения:

16.

17.

3. 18. 4

4. 19. 2

5. 2

Домашнее задание: решение заданий по образцу

Тема: Решение простейших тригонометрических

Материал для составления опорного конспекта:

Примеры решения задач

а) б)

3.Практическая часть урока. Решение №152,155,158б,159г.

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств вида cos t ≤ a , cos t ≥ a , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите уравнения.

1. cos x > — 1 1 . 2 cos (2x + )

2. cos 2 x > 0 1 2 . 2 cos (4x + )

3. cos 1

9. 2 cos (x — )

10. 2 cos (3x + ) 1

Домашнее задание: решение заданий по образцу

Урок . Решение неравенств вида

Материал для составления опорного конспекта:

x ( arc

Примеры решения задач

а) б)

3.Практическая часть урока.Решение №151,154,157а,в,158а,в.

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств вида sin t ≥ a , sin t ≤ a , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите неравенства:

1. sin x > — 13. 2 sin (2x + )

2. sin 2 x > 0 14. 2 sin (3x + ) 1

3. sin 6x )

7. 2

9. 2 sin x + 1 0

10. 2 sin x — 0

11. sin ( — x )

12. 2 sin (x — )

Домашнее задание: решение заданий по образцу

Урок. Решение неравенств вида

Материал для составления опорного конспекта:

Примеры решения задач

а) tg x б)

3.Практическая часть урока. Решение №153,156,158г,159б,

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите неравенства:

1. tg (x —

2. ctg (x +

3. tg ( 3x +

4. ctg (3x —

5. ctg (2x —

6. tg (2x –

9. 3 tg (2 x + )

10. √3 tg (6 x —

Домашнее задание: решение заданий по образцу

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств , закрепить умения применять полученные знания при решении неравенств различной степени сложности

Материал для составления опорного конспекта: