Решение тригонометрических уравнений урок презентация

«Урок-презентация» Решение тригонометрических уравнений, приводимых к алгебраическим
презентация к уроку по алгебре (10 класс) на тему

Урок «Решение тригонометрических уравнений, приводимых к алгебраическим». Урок входит в раздел «Тригонометрические функции» курса алгебры и начала анализа – 10 класс. Это урок объяснения нового материала, ему предшествует тема: «Решение простейших тригонометрических уравнений».

На уроке используется компьютерная презентация, цель которой помочь учащимся лучше разобраться в учебном материале. Презентация не громоздкая, она состоит из 22 слайдов. На слайдах представлен теоретический материал урока, подробно разобраны примеры решения тригонометрических уравнений. Также представлена геометрическая задача, решение в которой сводится к тригонометрическому уравнению. Представлены задания для самостоятельной работы разного уровня и приведены ответы к заданиям. Все задания максимально приближены к вариантам Единого Государственного Экзамена по математике. Презентация также содержит справочный материал.

Каждый слайд содержит гиперссылки, которые позволяют легко возвращаться от теоретического материала к примерам и заданиям. Слайды содержат минимум анимации, чтобы не отвлекать учащихся от основной задачи урока. Стоит также отметить, что данную компьютерную презентацию учащиеся могут использовать не только на данном уроке, но и дома в качестве справочного материала.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Владимирова Р.В. учитель математики МБОУ «Гимназия № 94» Московского района г.Казани Решение тригонометрических уравнений, приводимых к алгебраическим «Каждая решенная мною задача становится образом, который служит впоследствии для решения других задач» Р.Декарт

СОДЕРЖАНИЕ 1. Введение 2. Повторение Простейшие тригонометрические уравнения Частные случаи Задания для на повторение 4. Уравнения, приводимых к алгебраическим 5. Примеры решения уравнений 6. Использование тр.ур . при решении геометрических задач 7.Задания для самостоятельной работы 8.Краткий справочник формул 2

Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и есть тригонометрические функции, встречаются уже в III в. до н.э. в работах Евклида, Архимеда и других. Современную форму тригонометрическим функциям и вообще тригонометрии придал Леонард Эйлер. Ему принадлежат определения тригонометрических функций и принятая в наши дни символика. 1 3 Введение Содержание

ТРИГОНОМЕТРИЯ — математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ , с помощью которых связываются элементы треугольника, изучаются в курсе математического анализа. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ – это уравнения, в которых неизвестные являются аргументами тригонометрических функций. Введение 1 Содержание 4

Решение простейших тригонометрических уравнений Если уравнение не имеет решения. Если Если уравнение не имеет решения. Если 2 Содержание 5

Решение простейших тригонометрических уравнений Частные случаи 2 Содержание 6

1. Решите уравнение: 1) 2) 3) 4) 2. Решите уравнение : 1) 2) 3) 4) 3. Укажите наименьший положительный корень уравнения 1) 2) 3) 4) Задания на повторение 2 Содержание 7

Уравнения, приводимые к алгебраическим С помощью замены переменной можно привести тригонометрическое уравнение к алгебраическому. Рассмотрим несколько типов уравнений: Тип уравнения Замена Алгебраическое уравнение 4 Содержание 8 ПР №1 ПР №2 ПР №3 ПР №4

Делаем обратную замену , Пример 1 Уравнения, приводимые к алгебраическим Сделаем замену переменной Получаем : , 5 Содержание 9 Теория

Получаем : , Уравнения, приводимые к алгебраическим Сделаем замену переменной Применим основное тригонометрическое тождество 5 Пример 2 Содержание 10 Теория

Пример 3 Уравнения, приводимые к алгебраическим Сделаем замену переменной Получаем : , 5 Содержание 11 Теория

Получаем : , Пример 4 Уравнения, приводимые к алгебраическим Сделаем замену переменной 5 Содержание 12 Теория

6 Решение геометрической задачи Биссектриса одного из острых углов прямоугольного треугольника в шесть раз короче гипотенузы. Найдите острые углы этого треугольника. Содержание 13

ДАНО: треугольник АВС угол С –прямой ВД- биссектриса НАЙТИ : , РЕШЕНИЕ: Пусть Применив теорему синусов к треугольнику АВД, найдем, что Решение задачи Решение геометрической задачи Учитывая условия задачи, получаем: 6 14

Задача продолжение Решение геометрической задачи ОТВЕТ: 6 Решение задачи сводится к решению тригонометрического уравнения Решаем квадратное уравнение относительно ,получаем Содержание 15

Задания для самостоятельной работы Вариант № 1 Вариант № 2 1) 1) 2) 2) 3) 3) 4) 4) 5) 5) Уравнения, приводимые к алгебраическим 7 Содержание 16 Ответы

Ответы самостоятельной работы Вариант № 1 Вариант № 2 1) 1) 2) 2) 3) 3) 4) 4) 5) 5) Уравнения, приводимые к алгебраическим 7 Содержание 17 Задания

Краткий справочник формул 8 Нахождение тригонометрических функций по единичной окружности Основные тригонометрические тождества Формулы двойного аргумента Формулы сложения Формулы преобразования суммы в произведение Формулы преобразования произведения в сумму Содержание 18

Единичная окружность . . . 3 Содержание Задания на повторение 19 ПР №1 ПР №2 ПР №3 ПР №4 Задания с.р

2. Основные тригонометрические тождества 3.Формулы двойного аргумента 1 7 2 8 3 9 4 10 5 11 6 12 Краткий справочник формул 8 20

Краткий справочник формул 4. Формулы сложения 1 2 3 4 5 6 7 8 8 55 19

Краткий справочник формул 5. Формулы преобразования суммы в произведение 1 2 3 4 6. Формулы преобразования произведения в сумму 1 2 3 8 22

По теме: методические разработки, презентации и конспекты

Методическая разработка урока алгебры в 10 классе: «Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения»

Соотнести свое уравнение с одним из типов уравнений, используя справочный материал.

«Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения», 10 класс (профильный)

Материал презентации был представлен на защите урока на Всероссийском конкурсе «Мой лучший урок» (2 место).

«Тригонометрические уравнения, сводимые к алгебраическим»

Данные задания помогут учащимся при подготовке к ЕГЭ, а также на уроках по теме «Тригонометрические уравнения» для закрепления умений и навыков.

Методическая разработка урока на тему: Решение показательных уравнений, приводимых к квадратным, методом замены переменной.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА. На уроке рассматривались показательные уравнения, которые можно решить способом замены переменных. Класс, в котором проводился урок, характеризуется неустойчивостью внимани.

Рабочая программа элективного курса «Алгебра плюс: полиномиальные алгебраические уравнения. Нестандартные способы решения тригонометрических уравнений, неравенств, систем»

Программа состалена на основе авторской программы элективного курса «Алгебра плюс: элементарная алгебра с точки зрения высшей математики».

N16 Решение тригонометрических уравнений, приводимых к квадратному. за 2.05.20 для группы МЖКХ1 и за 4.05.20 для группы ПК1

Задание:1. Сделать конспект краткого справочного материала.2. Оформить решение типовых задач.3. Выполнить самостоятельно N1-N8.

26.04.2021 ПК1 Тема: «Решение тригонометрических уравнений, приводимых к квадратному».

Задание:1. Выполнить конспект краткого справочного материала по теме: » Решение тригонометрических уравнений, приводимых к квадратному».2. Оформить упражнения с решениями в тетради.3. Решить.

Тригонометрические уравнения и методы их решений. — презентация

Презентация была опубликована 6 лет назад пользователемФёдор Кавелин

Похожие презентации

Презентация на тему: » Тригонометрические уравнения и методы их решений.» — Транскрипт:

1 Тригонометрические уравнения и методы их решений

2 Тригонометрические уравнения — уравнения, содержащие неизвестное под знаком тригонометрической функции. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида решение полученного простейшего тригонометрического уравнения. Рассмотрим десять основных методов решения тригонометрических уравнений.

3 Содержание: 1. Алгебраический метод Алгебраический метод 2. Метод разложения на множители Метод разложения на множители 3. Метод вспомогательного угла Метод вспомогательного угла 4. Однородные уравнения Однородные уравнения 5. Универсальная подстановка Универсальная подстановка 6. Метод оценки Метод оценки 7. Метод понижения степени Метод понижения степени 8. Метод сравнения множеств Метод сравнения множеств 9. Переход к половинному углу Переход к половинному углу 10. Преобразование произведения в сумму Преобразование произведения в сумму

4 Алгебраический метод Этот метод нам хорошо известен из курса алгебры как метод замены переменной и подстановки.

5 Пример. Решить уравнение: 2cos 2 x-sinx+1=0 Решение. 2(1-sin 2 x)-sinx+1=0 -2sin 2 x-sinx+3=0 2sin 2 x+sinx-3=0 Пусть sinx=y, -1y1 2y 2 +y-3=0 y 1 =-1,5- не подходит по условию y 2 =1 Возвращаемся к старой переменной: sinx=1 x=/2+2k, k є Z

6 Метод разложения на множители Пример. Решить уравнение: sinx — sin2x = 0 Решение. sinx – 2sinx · cosx = 0 sinx(1- cosx) = 0 1. sinx=0 x=k, k є Z 2. 1-cosx=0 cosx=1 x=2n, n є Z Ответ: x=k, k є Z

7 Метод вспомогательного угла Пример. Решить уравнение: 3sinx-4cosx=5 Решение =25 25=5 5(3sinx/5-4cosx/5)=5 3sinx/5-4cosx/5=1 Т.к. (3/5) 2 +(4/5) 2 =1, то 3/5=cosφ φ=arccos(3/5) 4/5=sinφ φ=arcsin(4/5) sinxcosφ-cosxsinφ=1 sin(x-φ)=1 x-φ= /2+2k, k є Z x=/2+φ+2k, k є Z x=/2+arcsin(4/5)+2k, k є Z

8 Однородные уравнения Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо: а) перенести все его члены в левую часть; б) вынести все общие множители за скобки; в) приравнять все множители и скобки нулю; г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos ( или sin ) в старшей степени; д) решить полученное алгебраическое уравнение относительно tg.

9 Пример. Решить уравнение: 3sin 2 x + 4sinx · cosx + 5cos 2 x = 2. Решение. 3sin 2 x + 4sinx · cosx + 5cos 2 x = 2sin 2 x + 2cos 2 x sin 2 x + 4sinx · cosx + 3cos 2 x = 0 tg 2 x + 4tgx + 3 = 0, отсюда y 2 + 4y +3 = 0, корни этого уравнения: y 1 = -1, y 2 = -3, отсюда 1) tg x = –1, x=-/4+k, k є Z 2) tg x = –3, x=-arctg3+n, n є Z

10 Универсальная подстановка Универсальная подстановка применяется для тригонометрических уравнений, содержащих 2 и более тригонометрические функции. Пусть tg(x/2)=t, тогда sinx=2t/(1+t 2 ) (1) cosx=(1-t 2 )/(1+t 2 ) (2) tgx=2t/(1-t 2 ) В конце решения следует обязательно сделать проверку!

0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=» title=»Пример. Решить уравнение: 3sinx-4cosx=3 Решение. При помощи формул (1) и (2) произведем замену sinx и cosx и приведем выражение к общему знаменателю: (6t-4+4t 2 )/(1+t 2 )=3 Т.к. 1+t 2 >0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=» > 11 Пример. Решить уравнение: 3sinx-4cosx=3 Решение. При помощи формул (1) и (2) произведем замену sinx и cosx и приведем выражение к общему знаменателю: (6t-4+4t 2 )/(1+t 2 )=3 Т.к. 1+t 2 >0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=2arctg(-7)+2k, k є Z tg(x/2)=1 x=/2+2n, n є Z 0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=»> 0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=2arctg(-7)+2k, k є Z tg(x/2)=1 x=/2+2n, n є Z»> 0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=» title=»Пример. Решить уравнение: 3sinx-4cosx=3 Решение. При помощи формул (1) и (2) произведем замену sinx и cosx и приведем выражение к общему знаменателю: (6t-4+4t 2 )/(1+t 2 )=3 Т.к. 1+t 2 >0, то 4t 2 +6t-4=3+3t 2 t 2 +6t-7=0 t 1 =-7 t 2 =1 tg(x/2)=-7 x=»>

12 Метод оценки При решении некоторых тригонометрических уравнений иногда бывает полезно оценить значения тригонометрических функций, входящих в уравнение.

13 Пример. Решить уравнение: sinxsin5x=1 sinx=1 x=/2+2m, m є Z sin5x=1 — ? sin5(/2+2n)=1 sin(5/2+52n)=1 sin(5/2)=1 sin(/2)=1 — верно Ответ:x= /2+k, k є Z sinx=-1 x=-/2+2n, n є Z sin5x=-1 — ? sin5(-/2+2n)=-1 sin(-5/2+52n)=-1 sin(-5/2)=-1 sin(-/2)=-1 — sin(/2)=-1 — верно

14 Метод понижения степени Для решения уравнений данным методом применяются формулы понижения степени: 2sin 2 x=1-cos2x 2cos 2 x=1+cos2x

15 Пример. Решить уравнение: sin 4 x+cos 4 x= ½ sin 2 2x Решение. (sin 2 x) 2 +(cos 2 x) 2 = ½ sin 2 2x ¼ (1-2cos2x+cos 2 2x+1+2cos2x+cos 2 2x)= ½ (1-cos 2 2x) ½ (2+2cos 2 2x)=1-cos 2 2x 1+cos 2 2x= 1-cos 2 2x 2cos 2 2x=0 cos2x=0 2x=/2+k, k є Z x= /4+k/2, k є Z

16 Метод сравнения множеств Уравнения вида f(x)=φ(x) решаются методом сравнения множеств. Если Е(f) E(φ) – пустое множество, то уравнение не имеет решений Если Е(f) E(φ) состоит только из одной общей точки, то уравнение решается системой 2-х уравнений, левые части которых равны f и φ, а правые части равны значению общей точки.

17 Пример. Решить уравнение: 6cos 2 5x-5cosx+5,1=0 (1) Решение. 6cos 2 5x+5,1=5cosx (2) Пусть f(x)=6cos 2 5x+5,1 и φ(x)=5cosx. Е(f)=[5,1;11,1]-область значений функции f(x), Е(φ)=[-5;5]-область значений функции φ(x). Так как Е(f) E(φ) является пустое множество, то равенство (2) невозможно. Уравнение (2) решений не имеет, а, значит, и равносильное ему уравнение (1) тоже решений не имеет.

18 Переход к половинному углу При решении уравнений данным методом используются формулы двойного аргумента: sin2x=2sinxcosx cos2x=cos 2 x-sin 2 x В конце решения следует обязательно сделать проверку!

19 Пример. Решить уравнение: 2sinx–cosx=2. Решение. 4sin(x/2)·cos(x/2)-cos²(x/2)+sin²(x/2)= =2sin²(x/2)+2cos²(x/2) sin²(x/2)–4sin(x/2)·cos(x/2)+3cos²(x/2)=0 tg²(x/2)–4tg(x/2)+3=0 tg 1 (x/2)=1 x=/2+2k, k є Z tg 2 (x/2)=3 x=2arctg3+2k, k є Z

20 Преобразование произведения в сумму Данным методом решаются уравнения вида: 1. singxsingx=sinγxsinδx, если α+β=±(γ+δ) или α-β=±γ-δ 2. cosαxcosβx=cosγxcosδx, если α+β=±(γ+δ) или α-β=±γ-δ 3. singxsingx=cosγxcosδx, если α-β=±(γ+δ) 4. cosαxcosβx=sinγxsinδx, если α+β=γ±δ или α-β=γ±δ

21 Этот метод включает в себя применение формул: преобразования произведения в сумму: 2singsing=cos(α-β)-cos(α+β) 2cosαcosβ=cos(α+β)+cos(α-β) 2singcosβ=sin(α+β)+sin(α-β) 2cosαsing=sin(α+β)-sin(α-β) преобразования суммы в произведение: sing+sing=2sin((α+β)/2)cos((α-β)/2) sing-sing=2cos((α+β)/2)sin((α-β)/2) cosα+cosβ=2cos((α+β)/2)cos((α-β)/2) cosα-cosβ=-2sin((α+β)/2)sin((α-β)/2)

22 Пример. Решить уравнение: sinxsin5x=cos4x Решение. Преобразуем левую часть в сумму: ½ cos4x – ½ cos6x = cos4x ½ cos6x+ ½ cos4x= 0 cos6x+cos4x=0 Преобразуем левую часть в произведение: 2cos5xcosx=0 cos5xcosx=0 cos5x=0, x=/10+2k/5, k є Z cosx=0, x=/2+2n, n є Z. Ответ:x=/10+2k/5, k є Z

23 Презентацию подготовила ученица 11 «А» класса Мозжухина Софья

Презентация на тему : Методы решений тригонометрических уравнений.

Данная презентация предназначена для повторения и закрепления решений тригонометрических уравнений в 10-11 классах,в которой повторяются формулы тригонометрии и приведены примеры решений уравнений. Презентация может быть использована при подготовке к ЕГЭ (ПРОФИЛЬНЫЙ УРОВЕНЬ №13).

Просмотр содержимого документа
«Презентация на тему : Методы решений тригонометрических уравнений.»

Методы решения тригонометрических уравнений

• Метод замены переменной
• Метод разложения на множители
• Однородные тригонометрические уравнения
• С помощью тригонометрических формул:

• Формул сложения
• Формул приведения
• Формул двойного аргумента

Метод замены переменной

С помощью замены t = sinx или t = cosx, где t ∈ [−1;1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения.

См. примеры 1 – 3

Иногда используют универсальную тригонометрическую подстановку: t = tg

Метод разложения на множители

Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл:

f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0

и т.д. при условии существования каждого из сомножителей

См. примеры 4 – 5

Однородные тригонометрические уравнения

Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени .

a sin x + b cos x = 0

a sin x b cos x 0

Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0 .

Однородные тригонометрические уравнения

Уравнение вида a sin 2 x + b sin x cos x + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени .

a sin 2 x + b sin x cos x + c cos 2 x = 0

a sin 2 x b sin x cos x c cos 2 x 0

a tg 2 x + b tg x + c = 0

Далее, вводим новую переменную tg x = t и решаем методом замены переменной.

Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения

С помощью тригонометрических формул

cos (x − y) = cosx cosy + sinx siny

С помощью тригонометрических формул

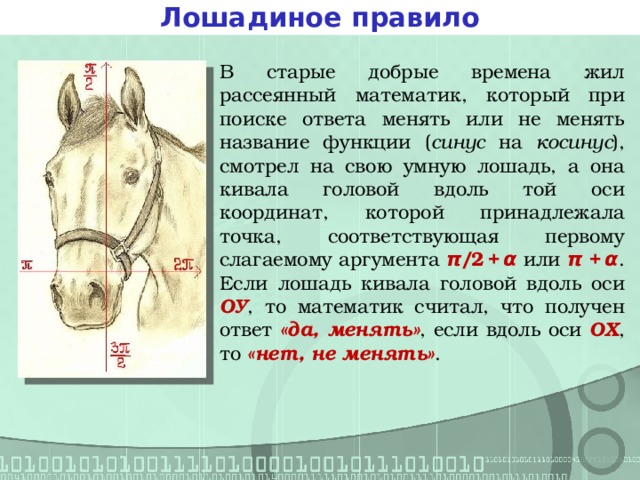
В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции ( синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α .

Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .

С помощью тригонометрических формул

3. Формулы двойного аргумента :