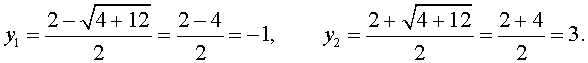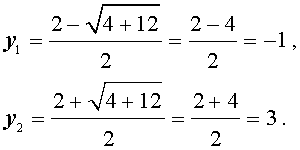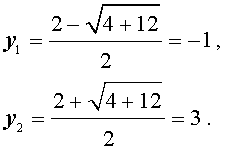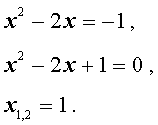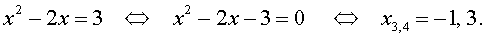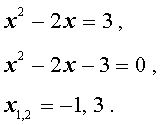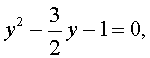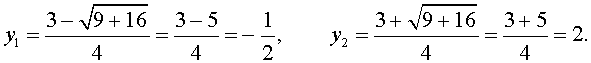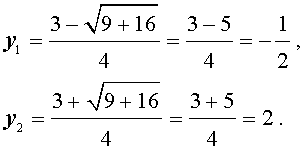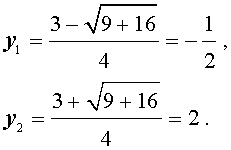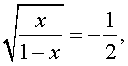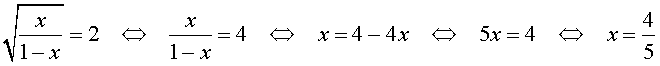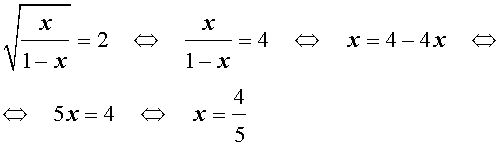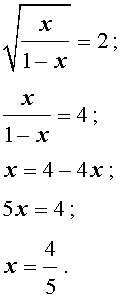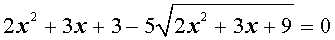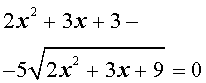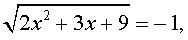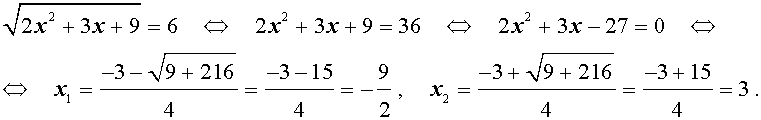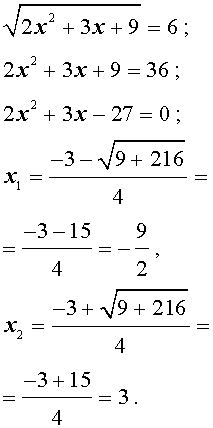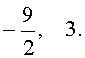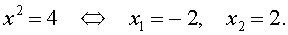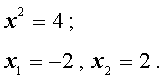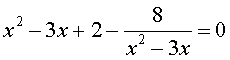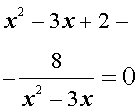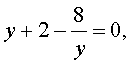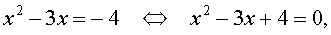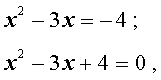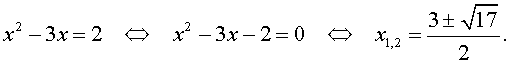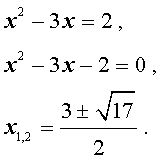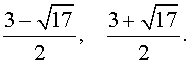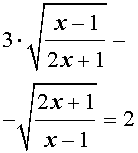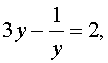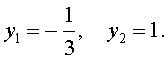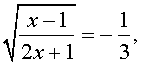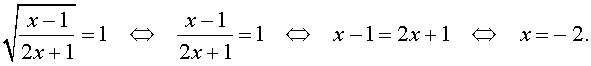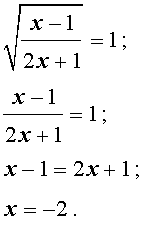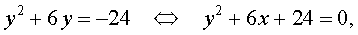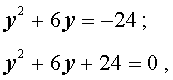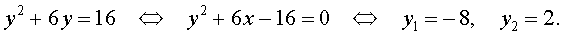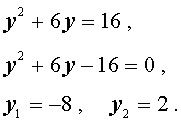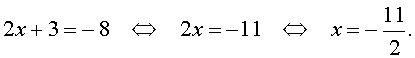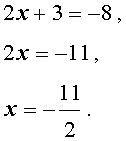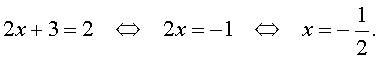Решение целых уравнений сводящихся к квадратным уравнениям

Решение уравнений, сводящихся к квадратным

Биквадратные уравнения

Биквадратным уравнением называется уравнение вида:

$$ ax^4+bx^2+c = 0, a \neq 0 $$

Алгоритм решения биквадратного уравнения

Шаг 1. Ввести новую переменную: $z = x^2 \ge 0$.

Переписать уравнение для новой переменной: $az^2+bz+c = 0$

Шаг 2. Решить полученное квадратное уравнение.

Если $D \gt 0$, $z_ <1,2>= \frac<-b \pm \sqrt> <2a>$. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.

Если D = 0,$z_0 = -\frac<2a>$. Проверить условие $z \ge 0$, если корень отрицательный, решений нет, переход на шаг 4.

Если $D \lt 0$, решений нет, переход на шаг 4.

Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = \pm \sqrt$.

Шаг 4. Работа завершена.

Шаг 1. $z = x^2 \ge 0, z^2+7z-30 = 0$

$z_1 = -10 \lt 0, z_2 = 3 \gt 0 $

Шаг 3. Находим корни из положительного $z: x_ <1,2>= \pm \sqrt<3>$

Метод разложения на множители

Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.

Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.

Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.

Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.

Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.

При разложении многочлена

• множители вида (x-a) называют линейными множителями ;
• множители вида $ (x^2+bx+c)$, для которых $D \lt 0$, называют неприводимыми квадратичными множителями .

Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.

Причём, такое представление единственно с точностью до порядка множителей.

Для разложения многочленов на множители применяются разные методы:

• вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
• группировка (см. §20 справочника для 7 класса);
• формулы сокращенного умножения (см. §25 справочника для 7 класса);
• метод неопределённых коэффициентов;
• выделение полного квадрата и т.п.

Решим уравнение $2x^3-x^2-8x+4 = 0$.

Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$

$$ (x^2-4)(2x-1) = 0 \Rightarrow (x-2)(x+2)(2x-1) = 0 $$

Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = \frac<1><2>$

Метод замены переменной

Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:

$Исходное \quad сложное \quad уравнение \iff <\left\< \begin Новая \quad переменная \quad (урав. \quad связи \quad со \quad старой \quad переменной \\ Исходное \quad урав. \quad в \quad «упрощ.» \quad виде \end \right.>$

Например, для биквадратных уравнений:

$$ ax^4+bx^2+c = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

Можно предложить аналогичные схемы для других уравнений:

$$ ax+b \sqrt+c = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

И, в общем виде, для любой рациональной степени n:

$$ ax^<2n>+bx^n+c = 0 \iff <\left\< \begin z = x^n \\ az^2+bz+c = 0 \end \right.> , n \in \Bbb Q $$

В других случаях замена переменной не настолько очевидна.

Но при удачном выборе, этот метод очень упрощает задачу.

Раскроем скобки:$ x^2-x = \frac<24>$. Сделаем замену:

$$ z = \frac<24> \Rightarrow z(z-2) = 24 \Rightarrow z^2-2z-24 = 0 \Rightarrow (z-6)(z+4) = 0 \Rightarrow \left[ \begin z_1 = -4 \\ z_2 = 6 \end \right.$$

Возвращаемся к исходной переменной x:

$$ \left[ \begin x^2-x = -4 \\ x^2-x = 6 \end \right. \Rightarrow \left[ \begin x^2-x+4 = 0 \\ x^2-x-6 = 0 \end \right. \Rightarrow \left[ \begin D \lt 0, x \in \varnothing \\ (x-3)(x+2) = 0 \end \right. \Rightarrow \left[ \begin x_1 = -2 \\ x_2 = 3 \end \right. $$

При использовании метода замены переменной не забывайте возвращаться к исходной переменной.

Выделение полного квадрата

Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:

$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$

Такое разложение не всегда возможно.

Рассмотрим выделение полного квадрата для квадратного трёхчлена:

$$ = a \Biggl(x+\frac <2a>\Biggr)^2 — \frac <4a>= a \Biggl(x+ \frac <2a>\Biggr)^2- \frac<4a>, D = b^2-4ac $$

Нами выделен полный квадрат $(x+\frac<2a>)^2$.

Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).

А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D \ge 0$.

Решить уравнение $x^4+4x^2-1 = 0$

Выделим полный квадрат и разложим на множители:

$$ \left[ \begin x^2+2-\sqrt <5>= 0 \\ x^2+2+\sqrt <5>= 0 \end \right. \Rightarrow \left[ \begin x^2 = \sqrt <5>-2 \gt 0 \\ x^2 = -(2+\sqrt<5>) \lt 0 \end \right. \Rightarrow x_1,2 = \pm \sqrt<\sqrt<5>-2> $$

Примеры

Пример 1. Решите биквадратные уравнения:

Делаем замену: $2x^4+7x^2-4 = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ 2z^2+7z-4 = 0 \end \right.>$

Решаем квадратное уравнение: $D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2$

$$ z = \frac<-7 \pm 9> <4>= \left[ \begin z_1 = -4 \lt 0 \\ z_2 = \frac<1> <2>\gt 0 \end \right. $$

Выбираем положительный z и возвращаемся к исходной переменной x:

Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 \iff <\left\< \begin z = (x+3)^2 \ge 0 \\ z^2-10z+24 = 0 \end \right.>$

Решаем квадратное уравнение: $z^2-10z+24 = 0 \Rightarrow (z-4)(z-6) = 0 \Rightarrow \left[ \begin z_1 = 4 \\ z_2 = 6 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x+3)^2 = 4 \\ (x+3)^2 = 6 \end \right. \Rightarrow \left[ \begin x+3 = \pm \sqrt <4>\\ x+3 = \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm 2 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_1 = -5 \\ x_2 = -1 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. $$

Пример 2. Решите уравнения аналогичные биквадратным:

Делаем замену: $x+4 \sqrt-60 = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ z^2+4z-60 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2+4z-60 = 0 \Rightarrow (z+10)(z-6) = 0 \Rightarrow \left[ \begin z_1 = -10 \\ z_2 = 6 \end \right.$

Выбираем положительный корень и возвращаемся к исходной переменной:

Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 \iff <\left\< \begin z = (x-1)^3 \\ z^2-7z-8 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2-7z-8 = 0 \Rightarrow (z+1)(z-8) = 0 \Rightarrow \left[ \begin z_1 = -1 \\ z_2 = 8 \end \right.$

При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x-1)^3 = -1 \\ (x-1)^3 = 8 \end \right. \Rightarrow \left[ \begin x-1 = -1 \\ x-1 = 2 \end \right. \Rightarrow \left[ \begin x_1 = 0 \\ x_2 = 3 \end \right. $$

Пример 3. Решите уравнения с помощью замены переменной:

Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:

$$ (x^2+6x)^2-(x^2+6x+9) = 33 \Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$

Решаем квадратное уравнение: $ z^2-z-42 = 0 \Rightarrow (z+6)(z-7) = 0 \Rightarrow \left[ \begin z_1 = -6 \\ z_2 = 7 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin x^2+6x = -6 \\ x^2+6x = 7 \end \right. \Rightarrow \left[ \begin x^2+6x+6 = 0 \\ x^2+6x-7=0 \end \right. \Rightarrow \left[ \begin D = 12, x = \frac<-6 \pm 2 \sqrt<3>> <2>\\ (x+7)(x-1) = 0 \end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm \sqrt <3>\\ x_3 = -7 \\ x_4 = 1 \end \right. $$

Делаем замену: $ \frac<4> + \frac<5> = 2 \iff \left[ \begin z = x^2+3 \ge 3 \\ \frac<4> + \frac<5> = 2 \end \right.$

Решаем уравнение относительно z:

$$ \frac<4> + \frac<5> = 2 \Rightarrow \frac<4(z+1)+5z> = \frac<2> <1>\Rightarrow 4(z+1)+5z = 2z(z+1) $$

$$ 2z^2+2z-9z-4 = 0 \Rightarrow 2z^2-7z-4 = 0 $$

$$ D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2 $$

$$ z = \frac<7 \pm 9> <4>= \left[ \begin z_1 = — \frac<1> <2>\lt 3 \\ z_2 = 4 \gt 3 \end \right. $$

Выбираем корень больше 3 и возвращаемся к исходной переменной:

$$ x^2+3 = 4 \Rightarrow x^2 = 1 \Rightarrow x_ <1,2>= \pm 1$$

Пример 4*. Решите уравнения:

Приведём это уравнение к биквадратному.

В линейных множителях (x+a) выберем все a =

Найдем их среднее арифметическое (см. §52 справочника для 7 класса)

Замена переменных $z = x+a_$:

Упрощаем уравнение, используя формулу разности квадратов:

$$ (z^2-9)(z^2-1) = 945 \Rightarrow z^4-10z^2+9 = 945 \Rightarrow z^4-10z^2-936 = 0 $$

Получили биквадратное уравнение.

Делаем замену: $z^4-10z^2-936 = 0 \iff <\left\< \begin t = z^2 \ge 0 \\ t^2-10t-936 = 0 \end \right.> $

Решаем квадратное уравнение:

$$ D = 100+4 \cdot 936 = 3844 = 62^2, t = \frac<10 \pm 62> <2>= \left[ \begin t_1 = -26 \lt 0 \\ t_2 = 36 \gt 0 \end \right. $$

Выбираем положительный корень и возвращаемся к переменной z:

$$ z = \pm \sqrt= \pm \sqrt <36>= \pm 6 $$

Возвращаемся к исходной переменной x:

$$ x = z-4 = \pm 6-4 = \left[ \begin x_1 = -10 \\ x_2 = 2 \end \right. $$

$$ z- \frac<1> =2,1 |\times z (z \neq 0) $$

$$ z^2-2,1z-1 = 0 \Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = \frac<2,1 \pm 2,9> <2>= \left[ \begin z_1 = -0,4 \\ z_2 = 2,5 \end \right. $$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin \frac = -0,4 \\ \frac = 2,5 \end \right. \Rightarrow \left[ \begin x^2+1 = -0,4x \\x^2+1 = 2,5x \end \right. \Rightarrow \left[ \begin x^2+0,4x+1 = 0 \\ x^2-2,5x+1 = 0 \end \right. $$

В первом уравнении $D = 0,4^2-4 \lt 0$, решений нет.

Во втором уравнении (x-2)(x-1/2) = 0 $\Rightarrow \left[ \begin x_1 = \frac<1> <2>\\ x_2 = 2 \end \right.$

Уравнения, сводящиеся к квадратным уравнениям:
трехчленные уравнения и уравнения вида
(ax + b)(ax + b + c)(ax +
+ b + 2c)(ax + b + 3c) = d , левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии

Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.

К таким уравнениям, в частности, относятся уравнения следующих типов:

	Трёхчленные уравнения
	Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
	Возвратные (симметричные) уравнения 3-ей степени
	Возвратные (симметричные) уравнения 4-ой степени
	Обобщенные возвратные уравнения 4-ой степени

Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .

Трехчленные уравнения

Трёхчленными уравнениями называют уравнения вида

а также уравнения вида

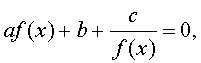(2)

где a, b, c – заданные числа, а f (x) – некоторая функция.

Для того, чтобы решить трехчленное уравнения вида (1), обозначим

тогда уравнение (1) станет квадратным уравнением относительно переменной y :

Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .

Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.

Покажем, как это осуществляется на примерах.

Пример 1 . Решить уравнение

Решение . Если обозначить

то уравнение (5) превратится в квадратное уравнение

В первом случае из равенства (6) получаем:

Во втором случае из равенства (6) получаем:

Пример 2 . Решить уравнение

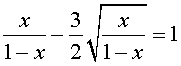(8)

Решение . Если обозначить

,

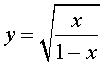(9)

то уравнение (8) превратится в квадратное уравнение

которое эквивалентно уравнению

В первом случае из равенства (9) получаем уравнение:

Во втором случае из равенства (9) получаем:

Ответ :

Пример 3 . Решить уравнение

Решение . Если обозначить

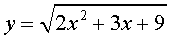(12)

то уравнение (11) превратится в квадратное уравнение

которое эквивалентно уравнению

В первом случае из равенства (12) получаем уравнение:

Во втором случае из равенства (12) получаем:

Ответ :

Пример 4 . Решить биквадратное уравнение

Решение . Если обозначить

то уравнение (14) превратится в квадратное уравнение

В первом случае из равенства (15) получаем уравнение:

которое решений не имеет.

Во втором случае из равенства (15) получаем:

Пример 5 . Решить уравнение

Решение . Если обозначить

уравнение (17) превращается в уравнение

которое при умножении на y принимает вид

В первом случае из равенства (18) получаем квадратное уравнение:

которое решений не имеет.

Во втором случае из равенства (18) получаем:

Ответ :

Пример 6 . Решить уравнение

Решение . Если обозначить

,

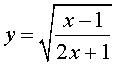(21)

уравнение (20) превращается в уравнение

которое при умножении на y принимает вид

В первом случае из равенства (21) получаем уравнение

Во втором случае из равенства (21) получаем:

Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии

где a, b, c, d – заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b , а разность равна c .

Схема решения уравнений вида (23) заключается в следующем.

Тогда уравнение (23) примет вид:

Перегруппируем сомножители в левой части уравнения (25) следующим образом:

Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:

Если теперь в уравнении (27) обозначить

то уравнение (27) станеи квадратным уравнением

Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно y , а затем в каждом из полученных случаев решить уравнение (24) относительно x .

Пример 7 . Решить уравнение

Решение .Если обозначить

уравнение (30) превращается в уравнение

Перегруппируем сомножители в левой части уравнения (32):

Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:

Если теперь обозначить

то уравнение (34) станет квадратным уравнением

В первом случае из равенства (35) получаем уравнение:

которое корней не имеет.

Во втором случае из равенства (35) получаем:

В первом из этих случаев, из равенства (31) получаем:

Во втором случае из равенства (31) получаем:

Ответ :

Рациональные уравнения. Семь типов рациональных уравнений, сводящихся к квадратным

В этой статье я покажу вам алгоритмы решения семи типов рациональных уравнений, которые с помощью замены переменных сводятся к квадратным. В большинстве случаев преобразования, которые приводят к замене, весьма нетривиальны, и самостоятельно о них догадаться достаточно трудно.

Для каждого типа уравнений я объясню, как в нем делать замену переменной, а затем в соответствующем видеоуроке покажу подробное решение.

У вас есть возможность продолжить решение уравнений самостоятельно, а затем сверить свое решение с видеоуроком.

1 . (x-1)(x-7)(x-4)(x+2)=40

Заметим, что в левой части уравнения стоит произведение четырех скобок, а в правой — число.

1. Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.

2. Перемножим их.

3. Введем замену переменной.

В нашем уравнении сгруппируем первую скобку с третьей, а вторую с четвертой,так как (-1)+(-4)=(-7)+2:

В этом месте замена переменной становится очевидной:

Получаем уравнение

Ответ: