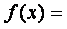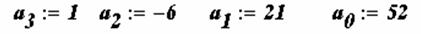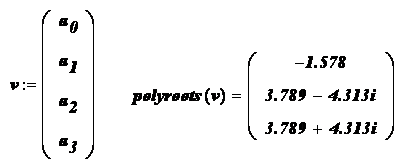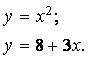решение уравнений маткад. Нелин_уравнения. Практическая работа 5 Численное решение нелинейных уравнений в Mathcad (метод простых итераций)
| Название | Практическая работа 5 Численное решение нелинейных уравнений в Mathcad (метод простых итераций) |
| Анкор | решение уравнений маткад |
| Дата | 24.02.2021 |
| Размер | 318.5 Kb. |
| Формат файла |  |
| Имя файла | Нелин_уравнения.doc |
| Тип | Практическая работа #179215 |
Подборка по базе: Самостоятельная работа по теме 3.doc, домашняя работа.docx, Лабораторная работа №11. Практическое изучение операционной сист, Лабораторная работа.docx, Лабораторная работа №12. Практическое изучение системы Astra Lin, Контрольная работа Кудрявцева.docx, Самостоятельная работа 1-1 История.docx, Практическая работа.docx, Большеорловская ШК. 6 класс. Исследовательская работа..doc, Практическая работа №5.docxПрактическая работа №5Цель работы:
Задание №1.Решить нелинейное уравнение методом итераций. Метод простых итераций является одним из наиболее важных способов численного решения уравнений. Этот метод состоит в следующем. Пусть дано уравнение где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения. Запишем уравнение (1) равносильным уравнением x= Выберем каким-либо способом, например графически, приближенное значение корня x0 и подставим его в правую часть уравнения (2). Получим некоторое число x1= Подставим теперь в правую часть уравнения (3) вместо x0 число x1. Получим новое число x2=
Задание №1.Решить нелинейное уравнение методом бисекции. Метод бисекции (половинного деления) состоит в следующем. Пусть дано уравнение Деление продолжать до получения отрезка длиной ε ≤ 10-3.
Если Подобная операция необходима для другого конца отрезка [ai, bi], для bi. Если Условный оператор if работает следующим образом. Если логическое выражение, записанное в скобках, истинно, то переменная слева от знака := принимает значение выражения или величины, стоящей первой после логического выражения, в противном случае переменной присваивается значение выражения, или величины, стоящей на втором месте после логического выражения.
Результат на экране: Л Локализация корня уравнения. Д Формулы для определения начала и конца отрезка и определения значения f(x) в середине отрезка. К Методом бисекции (половинного деления) уточнить корень уравнения.
Практическая работа №7Цель работы:
Задание №1.Решить нелинейное уравнение методом Ньютона. Знаменитый метод Ньютона является одним из наиболее эффективных способов численного решения нелинейных уравнений. Этот метод состоит в следующем. Пусть дано уравнение где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения с точностью ε. Расчетная формула метода Ньютона имеет следующий вид Выберем каким-либо способом, например, графически, приближенное значение корня x0 и, подставляя его в правую часть уравнения (2), можем начать итерационный процесс вычисления корня уравнения. Условием завершения итерационного процесса является выполнение условия В случае выполнения неравенства (3), корнем уравнения (1) будем считать значение xk+1. Найти действительные корни уравнения с точностью до трех значащих цифр.
x0:a.
Результат на экране: Нелинейное уравнение определено в виде функции. Локализация корней уравнения графическим способом. Приближенное значения корня уравнения. К Н Вычислительная формула Ньютона. Результат вычислений. Расчет погрешности вычислений. Погрешность вычислений становится допустимой на второй итерации Используя метод Ньютона, найти с точностью ε=10-6 положительный корень уравнений Метод простых итерацийДата добавления: 2015-07-23 ; просмотров: 7342 ; Нарушение авторских прав Лабораторная работа №5 Тема: Решение СЛАУ итерационным методом в MathCAD. Цель: изучение приемов численного решения систем линейных уравнений с помощью функций MathCAD. Порядок выполнения работы 1. Ознакомиться с теоретическими положениями. 2. Рассмотреть пример решения СЛАУ итерационным методом в MathCAD. 3. Выполнить практическое задание. 4. Ответить на контрольные вопросы. Содержание отчета 1. Тема, цель работы. 2. Практическое задание: 2.1. Постановка задачи. 2.2. Результаты выполнения. 3. Ответы на контрольные вопросы. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Итерационные методы – это методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.). Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода. Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса. Метод простых итераций Пусть дана линейная система (1).
Систему (1) коротко можно записать в виде матричного уравнения:
Предполагая, что диагональные коэффициенты разрешим первое уравнение системы (1) относительно х1, второе – относительно х2 и т. д. Тогда получим эквивалентную систему
Систему (3) можно записать в матричной форме x = b + ax, а любое (k + 1) приближение вычисляется по формуле
Напишем формулы приближений в развернутом виде:
Приведем достаточное условие сходимости метода итераций. Теорема:Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть
Следствие 1. Процесс итерации для системы (3) сходится, если: 1) Пример решения СЛАУ итерационным методом в MathCAD. Решить систему методом простых итераций:
|
Не нашли то, что искали? Google вам в помощь!
Решение нелинейных уравнений и систем уравнений в пакете MathCAD
Решение нелинейных уравнений
Вычисление корней численными методами включает два основных этапа:
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
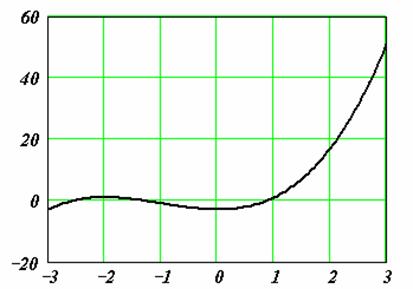
Пример. Дано алгебраическое уравнение
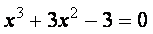
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
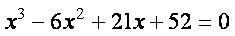
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции 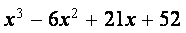
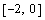
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. 

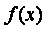
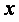
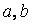
Пример. Используя функцию 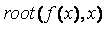
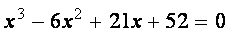
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной 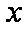
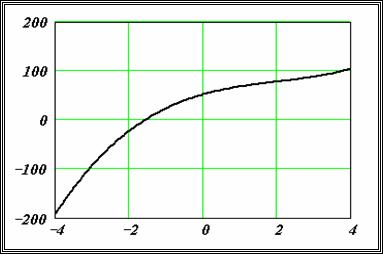
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения 
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка 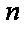
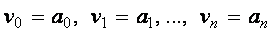
Пример. Используя функцию polyroots , найти все три корня уравнения 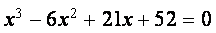
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
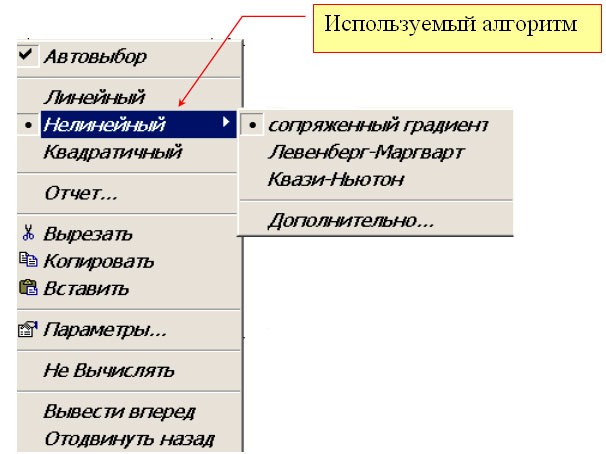
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения 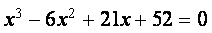
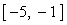
Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
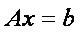
где 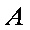
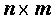
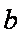

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию 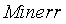
http://life-prog.ru/2_60054_metod-prostoy-iteratsii.html
http://pers.narod.ru/study/mathcad/07.html
 (x) (2)
(x) (2) , которое и будет корнем уравнения (2). Итерационный процесс xn=
, которое и будет корнем уравнения (2). Итерационный процесс xn=  . Критерием окончания итерационного процесса является выполнение неравенства
. Критерием окончания итерационного процесса является выполнение неравенства , где ε 3-x-1=0
, где ε 3-x-1=0
 .
. (знаки функции на концах разделенного отрезка разные), то начало нового отрезка для вычислений ai+1 совпадет с ai, т.е. ai+1=ai. В противном случае (знаки функции на концах разделенного отрезка одинаковые) ai+1 совпадет с точкой половинного деления отрезка, т.е.
(знаки функции на концах разделенного отрезка разные), то начало нового отрезка для вычислений ai+1 совпадет с ai, т.е. ai+1=ai. В противном случае (знаки функции на концах разделенного отрезка одинаковые) ai+1 совпадет с точкой половинного деления отрезка, т.е.  .
. , то конец нового отрезка для вычислений bi+1 совпадет с точкой половинного деления отрезка, т.е.
, то конец нового отрезка для вычислений bi+1 совпадет с точкой половинного деления отрезка, т.е.  ; в противном случае bi+1 совпадет с концом отрезка [ai, bi], т.е. bi+1=bi. Если же
; в противном случае bi+1 совпадет с концом отрезка [ai, bi], т.е. bi+1=bi. Если же  , то точка
, то точка  будет являться корнем нелинейного уравнения. Для реализации описанного процесса в Mathcad запишем формулы для определения начала и конца разделенного отрезка, воспользовавшись условным оператором if в векторной форме. Такая форма записи позволяет в вычислениях Mathcad использовать результаты предыдущих операций. Введем оператор вектора на три элемента и заполним его идентификаторами искомых величин ai+1, bi+1, gi (gi для вычисления
будет являться корнем нелинейного уравнения. Для реализации описанного процесса в Mathcad запишем формулы для определения начала и конца разделенного отрезка, воспользовавшись условным оператором if в векторной форме. Такая форма записи позволяет в вычислениях Mathcad использовать результаты предыдущих операций. Введем оператор вектора на три элемента и заполним его идентификаторами искомых величин ai+1, bi+1, gi (gi для вычисления  ). Введем знак присвоения и еще один оператор вектора на три элемента. Последний оператор заполните следующими формулами:
). Введем знак присвоения и еще один оператор вектора на три элемента. Последний оператор заполните следующими формулами:
 . Проанализируем значения вектора ε. Найдем элемент вектора, значение которого меньше заданной в условии задачи минимальной длины отрезка [ai,bi]. В нашем примере это значение элемента ε10. Корнем уравнения будет значение
. Проанализируем значения вектора ε. Найдем элемент вектора, значение которого меньше заданной в условии задачи минимальной длины отрезка [ai,bi]. В нашем примере это значение элемента ε10. Корнем уравнения будет значение  .
. евая часть нелинейного уравнения, определенная как функция f(x).
евая часть нелинейного уравнения, определенная как функция f(x).

 искретная переменная i.
искретная переменная i.
 Значения длины вычисляемых отрезков.
Значения длины вычисляемых отрезков.
 Длина отрезка [a10, b10] -3 .
Длина отрезка [a10, b10] -3 . начение f(x) наиболее близкое к нулю.
начение f(x) наиболее близкое к нулю. орень уравнения, который можно принять для десяти этапов деления отрезка.
орень уравнения, который можно принять для десяти этапов деления отрезка. с точностью до 0.0001.
с точностью до 0.0001. (2)
(2) (3)
(3)
 . Этим значением будет значение x=a в точке пересечения графика функции с осью абсцисс.
. Этим значением будет значение x=a в точке пересечения графика функции с осью абсцисс.

 . Результат вычислений погрешности выведите на экран. Корнем уравнения будет x2=1.171.
. Результат вычислений погрешности выведите на экран. Корнем уравнения будет x2=1.171.


 оличество итераций.
оличество итераций. ачальное значение неизвестного для решения уравнения.
ачальное значение неизвестного для решения уравнения.


 , поэтому допустимое решение получено на второй итерации
, поэтому допустимое решение получено на второй итерации  .
.

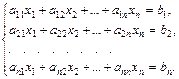
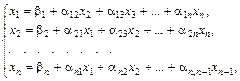
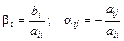 при i ¹ j
при i ¹ j
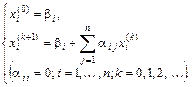
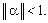
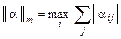 (k +1) .
(k +1) .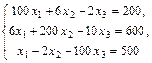
 Результат на экране:
Результат на экране: